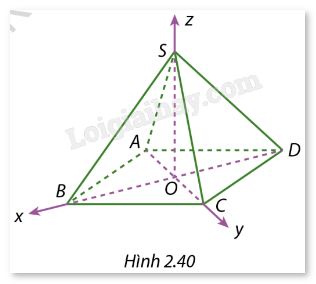
Giải bài tập 2.15 trang 73 SGK Toán 12 tập 1 - Cùng khám pháCho hình chóp tứ giác đều S.ABCD có O là giao điểm của AC và BD. Biết SA = a. SO = h. Xét hệ toạ độ Oxyz với các tia Ox, Oy, Oz tương ứng trùng với các tia OB, OC, OS như ở Hình 2.40. Hãy xác định toạ độ các điểm S, A, B, C, D. Đề bài Cho hình chóp tứ giác đều S.ABCD có O là giao điểm của AC và BD. Biết SA = a. SO = h. Xét hệ toạ độ Oxyz với các tia Ox, Oy, Oz tương ứng trùng với các tia OB, OC, OS như ở Hình 2.40. Hãy xác định toạ độ các điểm S, A, B, C, D.
Phương pháp giải - Xem chi tiết - Tính khoảng cách từ các đỉnh ABCD đến O. - Sử dụng tính chất của hình vuông, xác định tọa độ các đỉnh A, B, C, D. - Dựa vào chiều cao h của hình chóp (tức là độ dài đoạn SO) và độ dài SA = a, sử dụng hệ tọa độ Oxyz để xác định tọa độ của điểm S. Lời giải chi tiết Tam giác SOA vuông tại O nên: \(OA = \sqrt {S{A^2} - S{O^2}} = \sqrt {{a^2} - {h^2}} \) Vì ABCD là hình vuông nên: \(OA = OB = OC = OD = \sqrt {{a^2} - {h^2}} \) Toạ độ của các đỉnh A, B, C, D là: \(A = \left( {0, - \sqrt {{a^2} - {h^2}} ,0} \right);B = \left( {\sqrt {{a^2} - {h^2}} ,0,0} \right);C = \left( {0,\sqrt {{a^2} - {h^2}} ,0} \right);D = \left( { - \sqrt {{a^2} - {h^2}} ,0,0} \right)\) Điểm S có tọa độ \(S({x_S},{y_S},{z_S})\) với z_S = h và SA = a. Do điểm S nằm trên trục Oz, tọa độ của S trong hệ tọa độ Oxyz là (0, 0, h).  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
