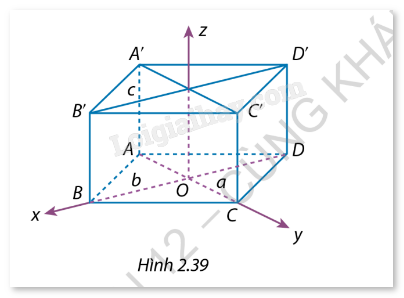
Giải bài tập 2.14 trang 73 SGK Toán 12 tập 1 - Cùng khám pháCho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình thoi. Hai đường chéo AC, BD của đáy có chiểu dài lần lượt là a, b. Cạnh bên AA’ = c. Hệ toạ độ Oxyz có gốc trùng với giao điểm O của hai đường chéo hình thoi ABCD, có tia Ox trùng với tia OB và tia Oy trùng với tia OC (Hinh 2.39). Hãy xác định: a) Toạ độ các đỉnh của hình hộp; b) Toạ độ vectơ \(\overrightarrow {B{D^\prime }} \). Đề bài Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình thoi. Hai đường chéo AC, BD của đáy có chiểu dài lần lượt là a, b. Cạnh bên AA’ = c. Hệ toạ độ Oxyz có gốc trùng với giao điểm O của hai đường chéo hình thoi ABCD, có tia Ox trùng với tia OB và tia Oy trùng với tia OC (Hinh 2.39). Hãy xác định: a) Toạ độ các đỉnh của hình hộp; b) Toạ độ vectơ \(\overrightarrow {B{D^\prime }} \).
Phương pháp giải - Xem chi tiết - Sử dụng gốc tọa độ tại giao điểm của hai đường chéo hình thoi, xác định tọa độ các đỉnh đáy dựa vào chiều dài các đường chéo. - Dùng công thức \(\overrightarrow {XY} = ({x_2} - {x_1},{y_2} - {y_1},{z_2} - {z_1})\) để tìm tọa độ vectơ \(\overrightarrow {BD'} \). Lời giải chi tiết a) Xác định tọa độ các đỉnh của hình hộp. \(B\left( {\frac{b}{2},0,0} \right),{\rm{ }}A\left( {0,\frac{{ - a}}{2},0} \right),C\left( {0,\frac{a}{2},0} \right){\rm{, }}D\left( {\frac{{ - b}}{2},0,0} \right)\) Tọa độ của các đỉnh A', B', C', D' lần lượt là: \(B'\left( {\frac{b}{2},0,c} \right),{\rm{ }}A'\left( {0,\frac{{ - a}}{2},c} \right),C'\left( {0,\frac{a}{2},c} \right){\rm{, }}D'\left( {\frac{{ - b}}{2},0,c} \right)\) b) Tọa độ vectơ \(\overrightarrow {BD'} :\) \(\overrightarrow {BD'} = D' - B = ( - \frac{b}{2},0,c) - (\frac{b}{2},0,0) = ( - b,0,c)\)  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
