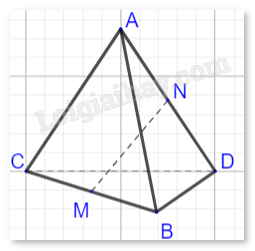
Giải bài tập 2.10 trang 65 SGK Toán 12 tập 1 - Cùng khám phá

Đề bài

Cho tứ diện ABCD có $AB = 2a,CD = 2a\sqrt 3$. Gọi M, N lần lượt là trung điểm của BC và AD. Biết rằng $MN = a\sqrt 7$, hãy tính góc giữa hai vectơ $\overrightarrow {AB}$ và $\overrightarrow {CD}$.

Lời giải chi tiết

- Vì $M$ là trung điểm của BC, nên $\overrightarrow {BM}  = \frac{1}{2}\overrightarrow {BC}$.

- Vì $N$ là trung điểm của AD, nên $\overrightarrow {AN}  = \frac{1}{2}\overrightarrow {AD}$.

- Vectơ $\overrightarrow {NM}$ có thể được viết là:

$\overrightarrow {NM}  = \overrightarrow {NB}  + \overrightarrow {BM}$

Với: $\overrightarrow {NB}  = \overrightarrow {NA}  + \overrightarrow {AB}  = \frac{1}{2}\overrightarrow {DA}  + \overrightarrow {AB}$

Và: $\overrightarrow {BM}  = \frac{1}{2}\overrightarrow {BC}  = \frac{1}{2}\left( {\overrightarrow {BD}  - \overrightarrow {CD} } \right)$.

Suy ra:

$\overrightarrow {NM}  = \frac{1}{2}\left( {\overrightarrow {DA}  + \overrightarrow {BD} } \right) + \overrightarrow {AB}  - \frac{1}{2}\overrightarrow {CD}  = \frac{1}{2}\overrightarrow {BA}  + \overrightarrow {AB}  - \frac{1}{2}\overrightarrow {CD}  = \frac{1}{2}(\overrightarrow {AB}  - \overrightarrow {CD} )$

Ta có: $\overrightarrow {NM}  \cdot \overrightarrow {NM}  = \frac{1}{4}(\overrightarrow {AB}  - \overrightarrow {CD} ) \cdot (\overrightarrow {AB}  - \overrightarrow {CD} )$

Biểu thức này mở rộng thành:

$\frac{1}{4}(\overrightarrow {AB}  \cdot \overrightarrow {AB}  - 2\overrightarrow {AB}  \cdot \overrightarrow {CD}  + \overrightarrow {CD}  \cdot \overrightarrow {CD} )$

Biết rằng $\overrightarrow {NM}  \cdot \overrightarrow {NM}  = M{N^2} = 7{a^2}$, $AB = 2a$, $CD = 2a\sqrt 3$, ta suy ra:

$7{a^2} = \frac{1}{4}(4{a^2} - 2\overrightarrow {AB}  \cdot \overrightarrow {CD}  + 12{a^2})$

$7{a^2} = \frac{1}{4}(16{a^2} - 2\overrightarrow {AB}  \cdot \overrightarrow {CD} )$

$28{a^2} = 16{a^2} - 2\overrightarrow {AB}  \cdot \overrightarrow {CD}$

$\overrightarrow {AB}  \cdot \overrightarrow {CD}  =  - 6{a^2}$

- Góc giữa hai vectơ được tính bởi:

$\cos \theta  = \frac{{\overrightarrow {AB}  \cdot \overrightarrow {CD} }}{{|\overrightarrow {AB} | \cdot |\overrightarrow {CD} |}}$

$\cos \theta  = \frac{{ - 6{a^2}}}{{2a.2a\sqrt 3 }} =  - \frac{{\sqrt 3 }}{2}$

Suy ra góc giữa $\overrightarrow {AB}$ và $\overrightarrow {CD}$ là $\theta  = {150^\circ }$.