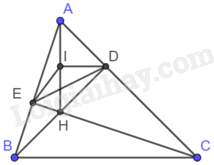
Giải bài 5.6 trang 59 sách bài tập toán 9 - Kết nối tri thức tập 1Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Chứng minh rằng: a) Bốn điểm A, E, H, D cùng thuộc một đường tròn. b) (AH > DE). Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Chứng minh rằng: a) Bốn điểm A, E, H, D cùng thuộc một đường tròn. b) AH>DE. Phương pháp giải - Xem chi tiết a) + Gọi I là trung điểm của AB. + Chứng minh IA=ID=IH=IE=12AH nên bốn điểm A, E, H, D cùng thuộc đường tròn tâm I đường kính AH. b) Vì góc EAD là góc nhọn nên dây DE là dây không đi qua tâm của đường tròn tâm I đường kính AH nên AH>DE. Lời giải chi tiết
a) Gọi I là trung điểm của AH. Vì BD và CE là hai đường cao của tam giác ABC nên BD⊥AC tại D, CE⊥AB tại E. Do đó, tam giác AEH vuông tại E và tam giác ADH vuông tại D. Tam giác AEH vuông tại E, có EI là đường trung tuyến nên IA=IE=IH=12AH(1) Tam giác ADH vuông tại D, có DI là đường trung tuyến nên IA=ID=IH=12AH(2) Từ (1) và (2) ta có: IA=ID=IH=IE=12AH. Do đó, bốn điểm A, E, H, D cùng thuộc đường tròn tâm I đường kính AH. b) Vì góc EAD là góc nhọn nên dây DE là dây không đi qua tâm của đường tròn đường kính AH nên AH>DE.
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|