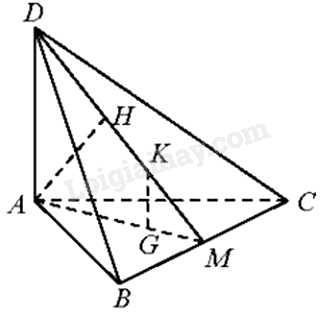
Giải bài 3 trang 55 sách bài tập toán 11 - Chân trời sáng tạo tập 2Cho tứ diện ABCD có DA⊥(ABC), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ AH⊥MD tại H. Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Cho tứ diện ABCD có DA⊥(ABC), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ AH⊥MD tại H. a) Chứng minh rằng AH⊥(BCD). b) Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Chứng minh rằng GK⊥(ABC). Phương pháp giải - Xem chi tiết a) Sử dụng kiến thức về định lí đường thẳng vuông góc với mặt phẳng để chứng minh: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (α) thì d⊥(α). b) Sử dụng kiến thức về liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng: Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia. Quảng cáo  Lời giải chi tiết
a) Vì DA⊥(ABC),BC⊂(ABC)⇒DA⊥BC Tam giác ABC cân tại A nên AM là đường trung tuyến đồng thời là đường cao, suy ra: BC⊥AM Vì DA⊥BC, BC⊥AM, DA và AM cắt nhau tại A và nằm trong (DAM) nên BC⊥(DAM). Lại có, AH⊂(DAM)⇒AH⊥BC Ta có: AH⊥MD, AH⊥BC, MD và BC cắt nhau tại M và nằm trong (BCD) nên AH⊥(BCD) b) Tam giác DBC có K là trọng tâm và DM là đường trung tuyến nên DKDM=23 Tam giác ABC có G là trọng tâm và AM là đường trung tuyến nên AGAM=23 Tam giác ADM có: DKDM=AGAM(=23) nên KG//AD (định lí Thalès đảo) Mà DA⊥(ABC) nên GK⊥(ABC).  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|
