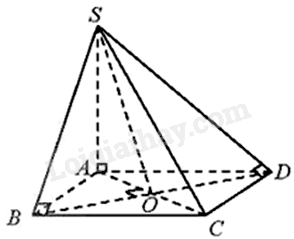
Giải bài 1 trang 73 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Đề bài

Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a, $SA$ $= a\sqrt 3$ và vuông góc với đáy. Xác định và tính góc giữa:

a) SB và (ABCD);

b) SC và (ABCD);

c) SD và (ABCD);

d) SB và (SAC).

Quảng cáo

Lời giải chi tiết

Vì $SA \bot \left( {ABCD} \right)$ nên A là hình chiếu của S trên mặt phẳng (ABCD).

a) Ta có: $\left( {SB,\left( {ABCD} \right)} \right)$ $= \left( {SB,AB} \right)$ $= \widehat {SBA}$

Vì $SA \bot \left( {ABCD} \right)$ $\Rightarrow SA \bot AB$. Do đó, tam giác SBA vuông tại A.

Suy ra: $\tan \widehat {SBA}$ $= \frac{{SA}}{{AB}}$ $= \frac{{a\sqrt 3 }}{a}$ $= \sqrt 3$ $\Rightarrow \widehat {SBA}$ $= {60^0}$

b) Ta có: $\left( {SC,\left( {ABCD} \right)} \right)$ $= \left( {SC,AC} \right)$ $= \widehat {SCA}$

Vì ABCD là hình vuông nên tam giác ACD vuông tại D.

Suy ra: $AC$ $= \sqrt {A{D^2} + D{C^2}}$ $= a\sqrt 2$ (định lí Pythagore)

Vì $SA \bot \left( {ABCD} \right)$ $\Rightarrow SA \bot AC$. Do đó, tam giác SCA vuông tại A.

Suy ra: $\tan \widehat {SCA}$ $= \frac{{SA}}{{AC}}$ $= \frac{{a\sqrt 3 }}{{a\sqrt 2 }}$ $= \frac{{\sqrt 6 }}{2}$ $\Rightarrow \widehat {SCA}$ $= 50,{8^0}$

c) Ta có: $\left( {SD,\left( {ABCD} \right)} \right)$ $= \left( {SD,AD} \right)$ $= \widehat {SDA}$

Vì $SA \bot \left( {ABCD} \right)$ $\Rightarrow SA \bot AD$. Do đó, tam giác SDA vuông tại A.

Suy ra: $\tan \widehat {SDA}$ $= \frac{{SA}}{{AD}}$ $= \frac{{a\sqrt 3 }}{a}$ $= \sqrt 3$ $\Rightarrow \widehat {SDA}$ $= {60^0}$

d) Vì ABCD là hình vuông nên $BO \bot AC$

Mà $SA \bot \left( {ABCD} \right)$ $\Rightarrow SA \bot BO$ nên $BO \bot \left( {SAC} \right)$

Do đó, O là hình chiếu của B trên mặt phẳng (SAC)

Do đó, $\left( {SB,\left( {SAC} \right)} \right)$ $= \left( {SB,SO} \right)$ $= \widehat {BSO}$

Tam giác SAB vuông tại A nên $SB$ $= \sqrt {A{B^2} + S{A^2}}$ $= \sqrt {{a^2} + {{\left( {a\sqrt 3 } \right)}^2}}$ $= 2a$ (định lí Pythagore)

Vì ABCD là hình vuông nên $OB$ $= \frac{1}{2}AC$ $= \frac{{a\sqrt 2 }}{2}$

Tam giác SBO vuông tại O nên $\sin \widehat {BSO}$ $= \frac{{OB}}{{SB}}$ $= \frac{{a\sqrt 2 }}{{2.2a}}$ $= \frac{{\sqrt 2 }}{4}$ $\Rightarrow \widehat {BSO} \approx 20,{7^0}$