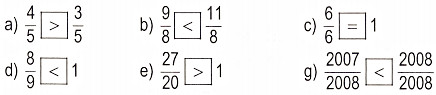
Bài tập cuối tuần Toán 4 tuần 22 - Đề 1 (Có đáp án và lời giải chi tiết)Tải vềBài tập cuối tuần 22 - Đề 1 bao gồm các bài tập chọn lọc với các dạng bài tập giúp các em ôn lại kiến thức đã học trong tuần Đề bài Bài 1. Rút gọn các phân số : \(\dfrac{{45}}{{135}}\;;\;\dfrac{{117}}{{234}}\;;\;\dfrac{{1515}}{{2727}}\;;\;\dfrac{{232323}}{{494949}}\). ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ Bài 2. So sánh hai phân số: a) \(\dfrac{3}{7}\) và \(\dfrac{5}{7}\) b) \(\dfrac{9}{8}\) và \(\dfrac{7}{8}\) c) \(\dfrac{3}{4}\) và \(\dfrac{5}{7}\) d) \(\dfrac{{17}}{{24}}\) và \(\dfrac{5}{8}\). ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ Bài 3. Điền dấu > ; < ; = thích hợp vào ô trống :
Bài 4. Hãy viết các phân số lần lượt bằng \(\dfrac{7}{{9\;}}\;,\;\dfrac{{11}}{{12}}\) và có mẫu số chung là 36. ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ Bài 5. Rút gọn rồi so sánh hai phân số a) \(\dfrac{{90}}{{126}}\) và \(\dfrac{6}{7}\) b) \(\dfrac{{75}}{{125}}\) và \(\dfrac{{35}}{{49}}\). ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ Lời giải chi tiết Câu 1. Phương pháp: Khi rút gọn phân số ta có thể làm như sau: - Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1. - Chia tử số và mẫu số cho số đó. Cứ làm như thế cho đến khi nhận được phân số tối giản. Cách giải: \(\dfrac{{45}}{{135}} = \dfrac{{45:45}}{{135:45}} = \dfrac{1}{3}\,;\) \(\dfrac{{117}}{{234}} = \dfrac{{117:117}}{{234:234}} = \dfrac{1}{2}\,\) \(\dfrac{{1515}}{{2727}} = \dfrac{{1515:303}}{{2727:303}} = \dfrac{5}{9}\,;\,\) \(\dfrac{{232323}}{{494949}} = \dfrac{{232323:10101}}{{494949:10101}} = \dfrac{{23}}{{49}}.\) Bài 2. Phương pháp: - Trong hai phân số có cùng mẫu số, phân số nào có tử số bé hơn thì bé hơn, phân số nào có tử số lớn hơn thì lớn hơn, nếu tử số bằng nhau thì hai phân số bằng nhau. - Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới. Cách giải: a) Vì 3 < 5 nên \(\dfrac{3}{7} < \dfrac{5}{7}\) ; b) Vì 9 > 7 nên \(\dfrac{9}{8} > \dfrac{7}{8}\); c) Ta có: \(\dfrac{3}{4} = \dfrac{{3 \times 7}}{{4 \times 7}} = \dfrac{{21}}{{28}};\) \(\dfrac{5}{7} = \dfrac{{5 \times 4}}{{7 \times 4}} = \dfrac{{20}}{{28}}.\) Vì 21 > 20 nên \(\dfrac{{21}}{{28}} > \dfrac{{20}}{{28}}\). Vậy: \(\dfrac{3}{4} > \dfrac{5}{7}\). d) Ta có: \(\dfrac{5}{8} = \dfrac{{5 \times 3}}{{8 \times 3}} = \dfrac{{15}}{{24}};\) Giữ nguyên phân số \(\dfrac{{17}}{{24}}\). Vì 17 > 15 nên \(\dfrac{{17}}{{24}} > \dfrac{{15}}{{24}}\) . Vậy: \(\dfrac{{17}}{{24}} > \dfrac{5}{8}\). Bài 3. Phương pháp: - Trong hai phân số có cùng mẫu số, phân số nào có tử số bé hơn thì bé hơn, phân số nào có tử số lớn hơn thì lớn hơn, nếu tử số bằng nhau thì hai phân số bằng nhau. - Phân số có tử số nhỏ hơn mẫu số thì nhỏ hơn 1. Phân số có tử số lớn hơn mẫu số thì lớn hơn 1. Phân số có tử số bằng mẫu số thì bằng 1. Cách giải:
Bài 4. Phương pháp: - Nhân cả tử và mẫu số của phân số \(\dfrac{7}{9}\) với 4 (vì 36 : 9 = 4). - Nhân cả tử và mẫu số của phân số \(\dfrac{{11}}{{12}}\) với 3 (vì 36 : 12 = 3). Cách giải: \(\dfrac{7}{9} = \dfrac{{7 \times 4}}{{9 \times 4}} = \dfrac{{28}}{{36}}\,;\) \(\dfrac{{11}}{{12}} = \dfrac{{11 \times 3}}{{12 \times 3}} = \dfrac{{33}}{{36}}.\) Vậy phân số lần lượt bằng \(\dfrac{7}{{9\;}}\;,\;\dfrac{{11}}{{12}}\) và có mẫu số chung là 36 là \(\dfrac{{28}}{{36}}\) và \(\dfrac{{33}}{{36}}\). Bài 5. Phương pháp: Rút gọn các phân số thành phân số tối giản (nếu được), sau đó có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới. Cách giải: a) Ta có: \(\dfrac{{90}}{{126}} = \;\dfrac{{90\;:\,\,\;18}}{{126\;:\;\,\,18}} = \;\dfrac{5}{7}\). Ta có: \(\dfrac{5}{7} < \dfrac{6}{7}\) (Vì 5 < 6). Vậy: \(\dfrac{{90}}{{126}} < \;\dfrac{6}{7}\). b) \(\dfrac{{75}}{{125}} = \dfrac{{75:25}}{{125:25}} = \dfrac{3}{5}\); \(\dfrac{{35}}{{49}} = \;\dfrac{{35\;:7}}{{49\;:7\;}} = \;\dfrac{5}{7}.\) Quy đồng mẫu số hai phân số \(\dfrac{3}{5}\) và \(\dfrac{5}{7}\) : \(\dfrac{3}{5} = \dfrac{{3 \times 7}}{{5 \times 7}} = \dfrac{{21}}{{35}};\) \(\dfrac{5}{7} = \dfrac{{5 \times 5}}{{7 \times 5}} = \dfrac{{25}}{{35}}.\) Ta có \(\dfrac{{21}}{{35}} < \dfrac{{25}}{{35}}\), hay \(\dfrac{3}{5} < \dfrac{5}{7}\). Vậy: \(\dfrac{{75}}{{125}} < \dfrac{{35}}{{49}}.\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K15 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
