Trắc nghiệm Bài 93: Ôn tập về phân số Toán 4 Cánh diềuĐề bài
Câu 1 :
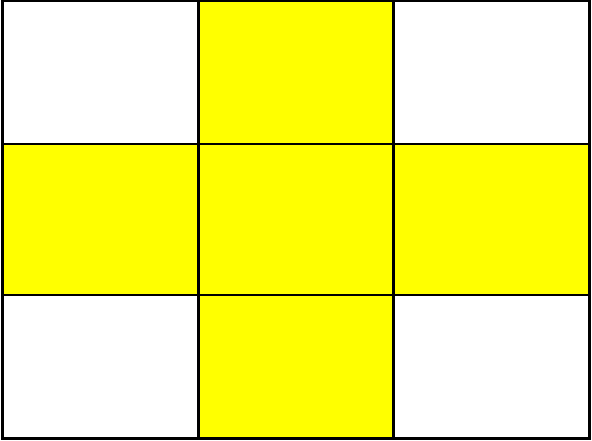
Cho hình vẽ như sau:
Phân số chỉ phần đã tô màu của hình đã cho là: A. \(\dfrac{4}{5}\) B. \(\dfrac{5}{4}\) C. \(\dfrac{4}{9}\) D. \(\dfrac{5}{9}\)
Câu 2 :
Rút gọn phân số \(\dfrac{{48}}{{72}}\) ta được phân số tối giản là: A. \(\dfrac{{12}}{{16}}\) B. \(\dfrac{{12}}{{18}}\) C. \(\dfrac{2}{3}\) D. \(\dfrac{3}{4}\)
Câu 3 :
Quy đồng mẫu số các phân số \(\dfrac{4}{5}\) và \(\dfrac{{17}}{{45}}\) ta được hai phân số \(\dfrac{a}{b}\) và \(\dfrac{{17}}{{45}}\). Khi đó: \(a=\) ; \(b=\)
Câu 4 :
Các phân số \(\dfrac{2}{3}\,;\,\,\dfrac{8}{7}\,;\,\,\dfrac{5}{6}\,;\,\,\dfrac{1}{2}\) viết theo thứ tự từ lớn đến bé là: A. \(\dfrac{5}{6}\,\,;\,\,\,\dfrac{2}{3}\,\,;\,\,\,\dfrac{8}{7}\,\,;\,\,\,\dfrac{1}{2}\) B. \(\,\,\dfrac{8}{7}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{2}{3}\,\,;\,\,\,\dfrac{1}{2}\) C. \(\,\,\dfrac{8}{7}\,\,;\,\,\,\dfrac{2}{3}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{1}{2}\) D. \(\,\,\dfrac{8}{7}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{1}{2}\,\,;\,\,\,\dfrac{2}{3}\,\,\)
Câu 5 :
Phép tính sau đúng hay sai? $\dfrac{1}{9} + \dfrac{4}{9} = \dfrac{{1 + 4}}{{9 + 9}} = \dfrac{5}{{18}}$ Đúng Sai
Câu 6 :
Ghép nối kết quả với phép tính tương ứng: \(\dfrac{1}{6} + \dfrac{2}{5}\) \(\dfrac{{11}}{{12}} - \dfrac{3}{4}\) \(\dfrac{8}{7}:\dfrac{4}{{3}}\) \(\dfrac{4}{9} \times \dfrac{{15}}{{14}}\) $\dfrac{6}{7}$ $\dfrac{{10}}{{21}}$ \(\dfrac{1}{6}\) \(\dfrac{{17}}{{30}}\,\)
Câu 7 :
A. \(\dfrac{{111}}{{10}}\) B. \(\dfrac{{41}}{{10}}\) C. \(\dfrac{{35}}{{24}}\) D. \(\dfrac{{155}}{{32}}\)
Câu 8 :
Tìm \(y\) biết: \(y:\dfrac{3}{7} = 2 + \dfrac{5}{8}\) A. \(y = \dfrac{3}{8}\) B. \(y = \dfrac{5}{7}\) C. \(y = \dfrac{9}{8}\) D. \(y = \dfrac{{49}}{8}\)
Câu 9 :
Điền số thích hợp vào ô trống: Khối lớp \(3\) có \(135\) học sinh. Khối lớp \(4\) có số học sinh bằng \(\dfrac{6}{5}\) số học sinh khối lớp \(3\). Vậy hai khối có tất cả học sinh.
Câu 10 :
Một tờ bìa hình chữ nhật có chiều dài \(\dfrac{4}{5}m\), chiều rộng kém chiều dài \(\dfrac{1}{4}m\). Người ta đã dùng hết \(\dfrac{1}{3}\) tờ bìa đó. Vậy diện tích phần tờ bìa còn lại là: A. \(\dfrac{{11}}{{75}}\,\,{m^2}\) B. \(\dfrac{{22}}{{75}}\,\,{m^2}\) C. \(\dfrac{{22}}{{25}}\,\,{m^2}\) D. \(\dfrac{{11}}{{25}}\,\,{m^2}\)
Câu 11 :
Một tấm vải dài \(60m\), người ta đã dùng \(\dfrac{3}{4}\) tấm vải đó để may quần áo. Số vải còn lại người ta đem may các túi, mỗi túi hết \(\dfrac{3}{4}m\) vải. Hỏi may được tất cả bao nhiêu cái túi như vậy? A. \(20\) cái B. \(22\) cái C. \(24\) cái D. \(28\) cái
Câu 12 :
Điền số thích hợp vào ô trống: Một mảnh đất hình chữ nhật có chiều dài \(36m\), chiều rộng bằng \(\dfrac{3}{4}\) chiều dài. Người ta sử dụng \(\dfrac{5}{9}\) diện tích để trồng hoa ly. Diện tích đất trồng hoa hồng chiếm \(\dfrac{2}{3}\) diện tích còn lại. Phần còn lại của mảnh đất được dùng để trồng hoa cúc. Vậy diện tích phần đất trồng hoa cúc là \({m^2}\).
Câu 13 :
Điền số thích hợp vào ô trống: $\frac{4}{5}\times \frac{5}{6}\times \frac{6}{7}\times \frac{7}{8}=\frac{?}{?}$
Câu 14 :
Diện tích của vườn hoa nhà trường được sử dụng như sau: \(\dfrac{4}{5}\) diện tích vườn hoa dùng để trồng các loại hoa, \(\dfrac{1}{6}\) diện tích vườn hoa để làm đường đi, diện tích phần còn lại để xây bể nước. $Vậy\ diện\ tích\ để\ xây\ bể\ nước\ chiếm\ \frac{?}{?}diện\ tích\ vườn\ hoa.$
Câu 15 :
Quy đồng mẫu số các phân số \(\dfrac{4}{5}\) và \(\dfrac{{17}}{{45}}\) ta được hai phân số là $\frac{?}{?}và\frac{17}{45}$
Lời giải và đáp án
Câu 1 :
Cho hình vẽ như sau:
Phân số chỉ phần đã tô màu của hình đã cho là: A. \(\dfrac{4}{5}\) B. \(\dfrac{5}{4}\) C. \(\dfrac{4}{9}\) D. \(\dfrac{5}{9}\) Đáp án
D. \(\dfrac{5}{9}\) Phương pháp giải :
Quan sát hình vẽ, tìm ô vuông được tô màu và tổng số ô vuông. Phân số chỉ phần đã tô màu của hình đã cho có tử số là số ô vuông được tô màu và mẫu số là tổng số ô vuông. Lời giải chi tiết :
Quan sát hình vẽ ta thấy có tất cả \(9\) ô vuông, trong đó có \(5\) ô vuông được tô màu. Vậy phân số chỉ số ô vuông đã tô màu trong hình là \(\dfrac{5}{9}\).
Câu 2 :
Rút gọn phân số \(\dfrac{{48}}{{72}}\) ta được phân số tối giản là: A. \(\dfrac{{12}}{{16}}\) B. \(\dfrac{{12}}{{18}}\) C. \(\dfrac{2}{3}\) D. \(\dfrac{3}{4}\) Đáp án
C. \(\dfrac{2}{3}\) Phương pháp giải :
Khi rút gọn phân số có thể làm như sau: - Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\). - Chia tử số và mẫu số cho số đó. Cứ làm như thế cho đến khi nhận được phân số tối giản. Lời giải chi tiết :
Rút gọn phân số ta có: \(\dfrac{{48}}{{72}} = \dfrac{{48:8}}{{72:8}} = \dfrac{6}{9} = \dfrac{{6:3}}{{9:3}} = \dfrac{2}{3}\) Vậy đáp án đúng là \(\dfrac{2}{3}\).
Câu 3 :
Quy đồng mẫu số các phân số \(\dfrac{4}{5}\) và \(\dfrac{{17}}{{45}}\) ta được hai phân số \(\dfrac{a}{b}\) và \(\dfrac{{17}}{{45}}\). Khi đó: \(a=\) ; \(b=\) Đáp án
Quy đồng mẫu số các phân số \(\dfrac{4}{5}\) và \(\dfrac{{17}}{{45}}\) ta được hai phân số \(\dfrac{a}{b}\) và \(\dfrac{{17}}{{45}}\). Khi đó: \(a=\) ; \(b=\) Phương pháp giải :
Ta thấy \(45:5 = 9\) nên chọn \(45\) là mẫu số chung. Ta quy đồng phân số \(\dfrac{4}{5}\) bằng cách nhân cả tử số và mẫu số với \(9\) và giữ nguyên phân số \(\dfrac{{17}}{{45}}\). Lời giải chi tiết :
Ta thấy \(45:5 = 9\) nên chọn \(45\) là mẫu số chung. Quy đồng mẫu số các phân số \(\dfrac{4}{5}\) và \(\dfrac{{17}}{{45}}\) như sau: \(\dfrac{4}{5} = \dfrac{{4 \times 9}}{{5 \times 9}} = \dfrac{{36}}{{45}}\); Giữ nguyên phân số \(\dfrac{{17}}{{45}}\). Quy đồng mẫu số các phân số \(\dfrac{4}{5}\) và \(\dfrac{{17}}{{45}}\) ta được hai phân số \(\dfrac{{36}}{{45}}\) và \(\dfrac{{17}}{{45}}\). Vậy đáp án đúng điền vào ô trống từ trái sang phải lần lượt là \(36\,;\,\,45\).
Câu 4 :
Các phân số \(\dfrac{2}{3}\,;\,\,\dfrac{8}{7}\,;\,\,\dfrac{5}{6}\,;\,\,\dfrac{1}{2}\) viết theo thứ tự từ lớn đến bé là: A. \(\dfrac{5}{6}\,\,;\,\,\,\dfrac{2}{3}\,\,;\,\,\,\dfrac{8}{7}\,\,;\,\,\,\dfrac{1}{2}\) B. \(\,\,\dfrac{8}{7}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{2}{3}\,\,;\,\,\,\dfrac{1}{2}\) C. \(\,\,\dfrac{8}{7}\,\,;\,\,\,\dfrac{2}{3}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{1}{2}\) D. \(\,\,\dfrac{8}{7}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{1}{2}\,\,;\,\,\,\dfrac{2}{3}\,\,\) Đáp án
B. \(\,\,\dfrac{8}{7}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{2}{3}\,\,;\,\,\,\dfrac{1}{2}\) Phương pháp giải :
- Áp dụng tính chất: Phân số có tử số lớn hơn mẫu số thì lớn hơn \(1\) ; phân số có tử số bé hơn mẫu số thì bé hơn \(1\) . - Quy đồng mẫu số các phân số rồi so sánh các phân số sau khi quy đồng. Trong hai phân số có cùng mẫu số, phân số có tử số lớn hơn thì lớn hơn. Lời giải chi tiết :
Ta có: \(\dfrac{2}{3}\,\, < \,\,\,1\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\dfrac{8}{7} > \,\,\,1\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{5}{6}\, < \,\,\,1\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{2} < \,\,\,1\,\) Ta sẽ so sánh các phân số \(\dfrac{2}{3}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{1}{2}\). Quy đồng mẫu số các phân số \(\dfrac{2}{3}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{1}{2}\)ta có: \(\dfrac{2}{3} = \dfrac{{2 \times 2}}{{3 \times 2}} = \dfrac{4}{6}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{2} = \dfrac{{1 \times 3}}{{2 \times 3}} = \dfrac{3}{6}\) ; Giữ nguyên phân số \(\,\dfrac{5}{6}\). Mà \(\,\,\dfrac{5}{6}\,\, > \,\,\,\dfrac{4}{6}\,\,\, > \,\,\,\dfrac{3}{6}\,\,\) Do đó \(\,\,\dfrac{5}{6}\,\,\, > \,\,\,\dfrac{2}{3}\,\,\, > \,\,\,\dfrac{1}{2}\) Suy ra \(\,\dfrac{8}{7}\,\, > \,\,\,\dfrac{5}{6}\,\,\, > \,\,\,\dfrac{2}{3}\,\,\, > \,\,\,\dfrac{1}{2}\) Vậy các phân số sắp xếp theo thứ tự từ lớn đến bé là \(\,\,\dfrac{8}{7}\,\,;\,\,\,\dfrac{5}{6}\,\,;\,\,\,\dfrac{2}{3}\,\,;\,\,\,\dfrac{1}{2}\).
Câu 5 :
Phép tính sau đúng hay sai? $\dfrac{1}{9} + \dfrac{4}{9} = \dfrac{{1 + 4}}{{9 + 9}} = \dfrac{5}{{18}}$ Đúng Sai Đáp án
Đúng Sai Phương pháp giải :
Dựa vào cách cộng hai phân số cùng mẫu số: Muốn cộng hai phân số cùng mẫu số, ta cộng các tử số và giữ nguyên mẫu số. Lời giải chi tiết :
Ta có: $\dfrac{1}{9} + \dfrac{4}{9} = \dfrac{{1 + 4}}{9} = \dfrac{5}{9}$ Vậy phép tính đã cho là sai.
Câu 6 :
Ghép nối kết quả với phép tính tương ứng: \(\dfrac{1}{6} + \dfrac{2}{5}\) \(\dfrac{{11}}{{12}} - \dfrac{3}{4}\) \(\dfrac{8}{7}:\dfrac{4}{{3}}\) \(\dfrac{4}{9} \times \dfrac{{15}}{{14}}\) $\dfrac{6}{7}$ $\dfrac{{10}}{{21}}$ \(\dfrac{1}{6}\) \(\dfrac{{17}}{{30}}\,\) Đáp án
\(\dfrac{1}{6} + \dfrac{2}{5}\) \(\dfrac{{17}}{{30}}\,\) \(\dfrac{{11}}{{12}} - \dfrac{3}{4}\) \(\dfrac{1}{6}\) \(\dfrac{8}{7}:\dfrac{4}{{3}}\) $\dfrac{6}{7}$ \(\dfrac{4}{9} \times \dfrac{{15}}{{14}}\) $\dfrac{{10}}{{21}}$ Phương pháp giải :
Xem lại quy tắc thực hiện các phép tính cộng, trừ, nhân, chia hai phân số để tính giá trị các phép tính, sau đó nối với kết quả tương ứng. Lời giải chi tiết :
Ta có: $\dfrac{1}{6} + \dfrac{2}{5} = \dfrac{5}{{30}} + \dfrac{{12}}{{30}} = \dfrac{{17}}{{30}}\,$ $\,\dfrac{{11}}{{12}} - \dfrac{3}{4} = \dfrac{{11}}{{12}} - \dfrac{9}{{12}} = \dfrac{2}{{12}} = \dfrac{1}{6}$ $\dfrac{8}{7}:\dfrac{4}{3} = \,\dfrac{8}{7} \times \dfrac{3}{4}\, = \dfrac{{8 \times 3}}{{7 \times 4}} = \dfrac{{4 \times 2 \times 3}}{{7 \times 4}} = \dfrac{6}{7}\,$ $\dfrac{4}{9} \times \dfrac{{15}}{{14}} = \dfrac{{4 \times 15}}{{9 \times 14}} = \dfrac{{2 \times 2 \times 5 \times 3}}{{3 \times 3 \times 7 \times 2}} = \dfrac{{10}}{{21}}\,.$
Câu 7 :
A. \(\dfrac{{111}}{{10}}\) B. \(\dfrac{{41}}{{10}}\) C. \(\dfrac{{35}}{{24}}\) D. \(\dfrac{{155}}{{32}}\) Đáp án
B. \(\dfrac{{41}}{{10}}\) Phương pháp giải :
Biểu thức có phép cộng và phép chia thì ta thực hiện phép tính chia trước, phép tính cộng sau. Lời giải chi tiết :
Ta có: \(5 - \dfrac{3}{8}:\dfrac{5}{{12}} = 5 - \dfrac{3}{8} \times \dfrac{{12}}{5} = 5 - \dfrac{{3 \times 12}}{{8 \times 5}} \) \(= 5 - \dfrac{{3 \times 4 \times 3}}{{4 \times 2 \times 5}} = 5 - \dfrac{9}{{10}} = \dfrac{{50}}{{10}} - \dfrac{9}{{10}} = \dfrac{{41}}{{10}}\) Vậy đáp án đúng là \(\dfrac{{41}}{{10}}\).
Câu 8 :
Tìm \(y\) biết: \(y:\dfrac{3}{7} = 2 + \dfrac{5}{8}\) A. \(y = \dfrac{3}{8}\) B. \(y = \dfrac{5}{7}\) C. \(y = \dfrac{9}{8}\) D. \(y = \dfrac{{49}}{8}\) Đáp án
C. \(y = \dfrac{9}{8}\) Phương pháp giải :
- Tính giá trị vế phải. - \(y\) ở vị trí số bị chia, muốn tìm số bị chia ta lấy thương nhân với số chia. Lời giải chi tiết :
\(\begin{array}{l}y:\dfrac{3}{7} = 2 + \dfrac{5}{8}\\y:\dfrac{3}{7} = \dfrac{{16}}{8} + \dfrac{5}{8}\\y:\dfrac{3}{7} = \dfrac{{21}}{8}\\y = \dfrac{{21}}{8} \times \dfrac{3}{7}\\y = \dfrac{9}{8}\end{array}\) Vậy đáp án đúng là \(y = \dfrac{9}{8}\).
Câu 9 :
Điền số thích hợp vào ô trống: Khối lớp \(3\) có \(135\) học sinh. Khối lớp \(4\) có số học sinh bằng \(\dfrac{6}{5}\) số học sinh khối lớp \(3\). Vậy hai khối có tất cả học sinh. Đáp án
Khối lớp \(3\) có \(135\) học sinh. Khối lớp \(4\) có số học sinh bằng \(\dfrac{6}{5}\) số học sinh khối lớp \(3\). Vậy hai khối có tất cả học sinh. Phương pháp giải :
- Tìm số học sinh khối lớp \(4\) ta lấy số học sinh khối lớp \(3\) nhân với \(\dfrac{6}{5}\). - Số học sinh của cả hai khối = số học sinh khối lớp \(3\) + số học sinh khối lớp \(4\). Lời giải chi tiết :
Khối lớp \(4\) có số học sinh là: \(135 \times \dfrac{6}{5} = 162\) (học sinh) Hai khối có tất cả học sinh là: \(135 + 162 = 297\) (học sinh) Đáp số: \(297\) học sinh. Vậy đáp án đúng điền vào ô trống là \(297\).
Câu 10 :
Một tờ bìa hình chữ nhật có chiều dài \(\dfrac{4}{5}m\), chiều rộng kém chiều dài \(\dfrac{1}{4}m\). Người ta đã dùng hết \(\dfrac{1}{3}\) tờ bìa đó. Vậy diện tích phần tờ bìa còn lại là: A. \(\dfrac{{11}}{{75}}\,\,{m^2}\) B. \(\dfrac{{22}}{{75}}\,\,{m^2}\) C. \(\dfrac{{22}}{{25}}\,\,{m^2}\) D. \(\dfrac{{11}}{{25}}\,\,{m^2}\) Đáp án
B. \(\dfrac{{22}}{{75}}\,\,{m^2}\) Phương pháp giải :
- Tính chiều rộng tờ bìa ta lấy số đo chiều dài trừ đi \(\dfrac{1}{4}m\). - Tính diện tích tờ bìa ta lấy chiều dài nhân với chiều rộng. - Tính diện tích phần tờ bìa đã dùng ta lấy diện tích nhân với \(\dfrac{1}{3}\). - Tính diện tích phần tờ bìa còn lại ta lấy diện tích tờ bìa trừ đi diện tích phần tờ bìa đã dùng. Lời giải chi tiết :
Chiều rộng tờ bìa đó là: \(\dfrac{4}{5} - \dfrac{1}{4} = \dfrac{{11}}{{20}}\,\,(m)\) Diện tích tờ bìa đó là: \(\dfrac{4}{5} \times \dfrac{{11}}{{20}} = \dfrac{{11}}{{25}}\,\,({m^2})\) Diện tích phần tờ bìa đã dùng là: \(\dfrac{{11}}{{25}} \times \dfrac{1}{3} = \dfrac{{11}}{{75}}\,\,({m^2})\) Diện tích phần tờ bìa còn lại là: \(\dfrac{{11}}{{25}} - \dfrac{{11}}{{75}} = \dfrac{{22}}{{75}}\,\,({m^2})\) Đáp số: \(\dfrac{{22}}{{75}}\,\,{m^2}\).
Câu 11 :
Một tấm vải dài \(60m\), người ta đã dùng \(\dfrac{3}{4}\) tấm vải đó để may quần áo. Số vải còn lại người ta đem may các túi, mỗi túi hết \(\dfrac{3}{4}m\) vải. Hỏi may được tất cả bao nhiêu cái túi như vậy? A. \(20\) cái B. \(22\) cái C. \(24\) cái D. \(28\) cái Đáp án
A. \(20\) cái Phương pháp giải :
- Tính số vải dùng để may quần áo ta lấy tổng số mét vải nhân với \(\dfrac{3}{4}\). - Tính số vải dùng để may túi ta lấy tổng số mét vải trừ đi số vải dùng để may quần áo. - Tìm số túi được may ta lấy số vải dùng để may túi chia cho số mét vải để may \(1\) cái túi. Lời giải chi tiết :
Người ta may quần áo hết số mét vải là: \(60 \times \dfrac{3}{4} = 45\,\,(m)\) Số vải dùng để may túi là: \(60 - 45\, = 15\,(m)\) May được tất cả số cái túi là: \(15:\dfrac{3}{4} = 20\) (cái) Đáp số: \(20\) cái.
Câu 12 :
Điền số thích hợp vào ô trống: Một mảnh đất hình chữ nhật có chiều dài \(36m\), chiều rộng bằng \(\dfrac{3}{4}\) chiều dài. Người ta sử dụng \(\dfrac{5}{9}\) diện tích để trồng hoa ly. Diện tích đất trồng hoa hồng chiếm \(\dfrac{2}{3}\) diện tích còn lại. Phần còn lại của mảnh đất được dùng để trồng hoa cúc. Vậy diện tích phần đất trồng hoa cúc là \({m^2}\). Đáp án
Một mảnh đất hình chữ nhật có chiều dài \(36m\), chiều rộng bằng \(\dfrac{3}{4}\) chiều dài. Người ta sử dụng \(\dfrac{5}{9}\) diện tích để trồng hoa ly. Diện tích đất trồng hoa hồng chiếm \(\dfrac{2}{3}\) diện tích còn lại. Phần còn lại của mảnh đất được dùng để trồng hoa cúc. Vậy diện tích phần đất trồng hoa cúc là \({m^2}\). Phương pháp giải :
- Tìm chiều rộng của mảnh đất, tức là ta tìm \(\dfrac{3}{4}\) của \(36m\), ta lấy \(36m\) nhân với \(\dfrac{3}{4}\). - Tìm diện tích cả mảnh đất hình chữ nhật ta lấy chiều dài nhân với chiều rộng. - Tìm diện tích dùng để trồng hoa ly, tức là ta tìm \(\dfrac{5}{9}\) của diện tích, ta lấy diện tích nhân với \(\dfrac{5}{9}\). - Tìm diện tích phần đất còn lại sau khi trồng hoa ly ta lấy diện tích cả mảnh đất trừ đi diện tích đất trồng hoa lan. - Tìm diện tích dùng để trồng hoa hồng, ta lấy diện tích phần đất còn lại sau khi trồng hoa ly nhân với \(\dfrac{2}{3}\). - Tìm diện tích dùng để trồng hoa cúc ta lấy diện tích mảnh đất trừ đi tổng diện tích đất trồng hoa ly và diện tích trồng hoa hồng. Lời giải chi tiết :
Chiều rộng mảnh đất đó là: \(36 \times \dfrac{3}{4} = 27\,\,(m)\) Diện tích mảnh đất hình chữ nhật là: \(36 \times 27 = 972\,\,({m^2})\) Diện tích trồng hoa ly là: \(972\, \times \dfrac{5}{9}\, = 540\,\,({m^2})\) Diện tích phần đất còn lại sau khi trồng hoa ly là: \(972\, - 540 = 432\,\,({m^2})\) Diện tích trồng hoa hồng là: \(432\, \times \dfrac{2}{3}\, = 288\,\,({m^2})\) Diện tích trồng hoa cúc là: \(972\, - (540 + 288) = 144\,\,({m^2})\) Đáp số: \(144{m^2}\). Vậy đáp án đúng điền vào ô trống là \(144\) .
Câu 13 :
Điền số thích hợp vào ô trống: $\frac{4}{5}\times \frac{5}{6}\times \frac{6}{7}\times \frac{7}{8}=\frac{?}{?}$
Đáp án
$\frac{4}{5}\times \frac{5}{6}\times \frac{6}{7}\times \frac{7}{8}=\frac{1}{2}$
Phương pháp giải :
Muốn nhân các phân số ta nhân các tử số với nhau, nhân các mẫu số với nhau. Lời giải chi tiết :
Ta có: $\dfrac{4}{5} \times \dfrac{5}{6} \times \dfrac{6}{7} \times \dfrac{7}{8} = \dfrac{{4 \times 5 \times 6 \times 7}}{{5 \times 6 \times 7 \times 8}} = \dfrac{{4 \times 5 \times 6 \times 7}}{{5 \times 6 \times 7 \times 4 \times 2}} = \dfrac{1}{2}$ Vậy đáp án đúng điền vào ô trống từ trên xuống dưới lần lượt là \(1\,;\,\,2\).
Câu 14 :
Diện tích của vườn hoa nhà trường được sử dụng như sau: \(\dfrac{4}{5}\) diện tích vườn hoa dùng để trồng các loại hoa, \(\dfrac{1}{6}\) diện tích vườn hoa để làm đường đi, diện tích phần còn lại để xây bể nước. $Vậy\ diện\ tích\ để\ xây\ bể\ nước\ chiếm\ \frac{?}{?}diện\ tích\ vườn\ hoa.$
Đáp án
$Vậy\ diện\ tích\ để\ xây\ bể\ nước\ chiếm\ \frac{1}{30}diện\ tích\ vườn\ hoa.$
Phương pháp giải :
- Coi diện tích vườn hoa là \(1\) đơn vị. - Tính tổng diện tích phần đất để trồng các loại hoa và phần đất để làm đường đi. - Tính diện tích phần đất để xây bể nước ta lấy \(1\) trừ đi đi tổng diện tích phần đất để trồng các loại hoa và phần đất để làm đường đi. Lời giải chi tiết :
Coi diện tích vườn hoa là \(1\) đơn vị. Diện tích phần đất để trồng các loại hoa và phần đất để làm đường đi chiếm số phần diện tích vườn hoa là: \(\dfrac{4}{5} + \dfrac{1}{6} = \dfrac{{29}}{{30}}\) (diện tích vườn hoa) Diện tích để xây bể nước chiếm số phần diện tích vườn hoa là: \(1 - \dfrac{{29}}{{30}} = \dfrac{1}{{30}}\) (diện tích vườn hoa) Đáp số: \(\dfrac{1}{{30}}\) diện tích vườn hoa. Vậy đáp án đúng điền vào ô trống từ trên xuống dưới lần lượt là \(1\,;\,\,30\).
Câu 15 :
Quy đồng mẫu số các phân số \(\dfrac{4}{5}\) và \(\dfrac{{17}}{{45}}\) ta được hai phân số là $\frac{?}{?}và\frac{17}{45}$
Đáp án
$\frac{36}{45}và\frac{17}{45}$
Phương pháp giải :
Ta thấy \(45:5 = 9\) nên chọn \(45\) là mẫu số chung. Ta quy đồng phân số \(\dfrac{4}{5}\) bằng cách nhân cả tử số và mẫu số với \(9\) và giữ nguyên phân số \(\dfrac{{17}}{{45}}\). Lời giải chi tiết :
Ta thấy \(45:5 = 9\) nên chọn \(45\) là mẫu số chung. Quy đồng mẫu số các phân số \(\dfrac{4}{5}\) và \(\dfrac{{17}}{{45}}\) như sau: \(\dfrac{4}{5} = \dfrac{{4 \times 9}}{{5 \times 9}} = \dfrac{{36}}{{45}}\); Giữ nguyên phân số \(\dfrac{{17}}{{45}}\). Quy đồng mẫu số các phân số \(\dfrac{4}{5}\) và \(\dfrac{{17}}{{45}}\) ta được hai phân số \(\dfrac{{36}}{{45}}\) và \(\dfrac{{17}}{{45}}\). Vậy đáp án đúng điền vào ô trống từ trái sang phải lần lượt là \(36\,;\,\,45\).
|
Điền số thích hợp vào ô trống:
.jpg)
.jpg)
