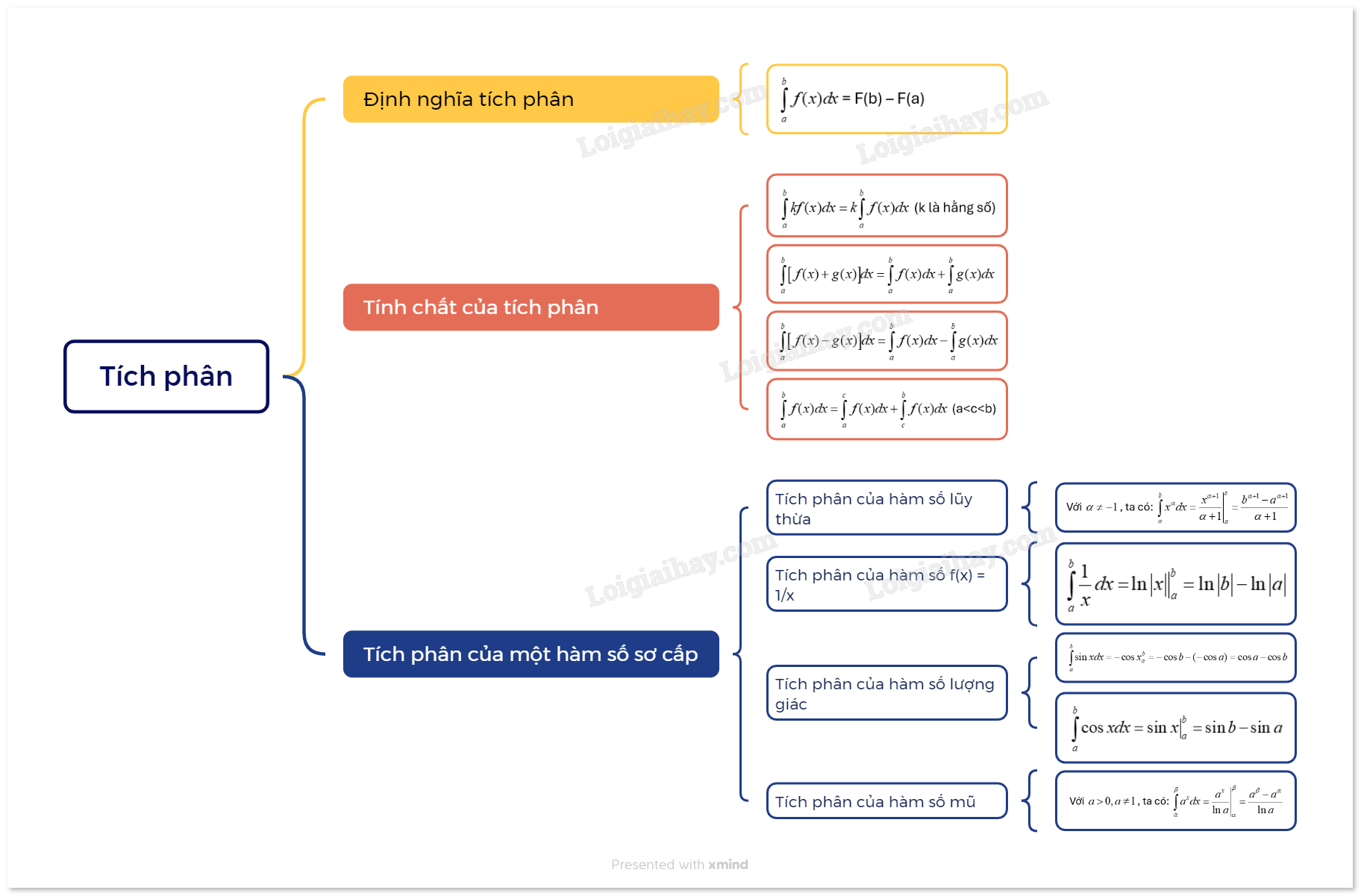
Lý thuyết Lý thuyết Tích phân Toán 12 Cánh DiềuCho hàm số f(x) liên tục trên đoạn (left[ {a;b} right]). Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn (left[ {a;b} right]) thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là (intlimits_a^b {f(x)dx} ). 1.Định nghĩa tích phân
2. Tính chất của tích phân
3. Tích phân của một số hàm số sơ cấp
b) Tích phân của hàm số f(x)=1x
c) Tích phân của hàm số lượng giác
d) Tích phân của hàm số mũ
|













