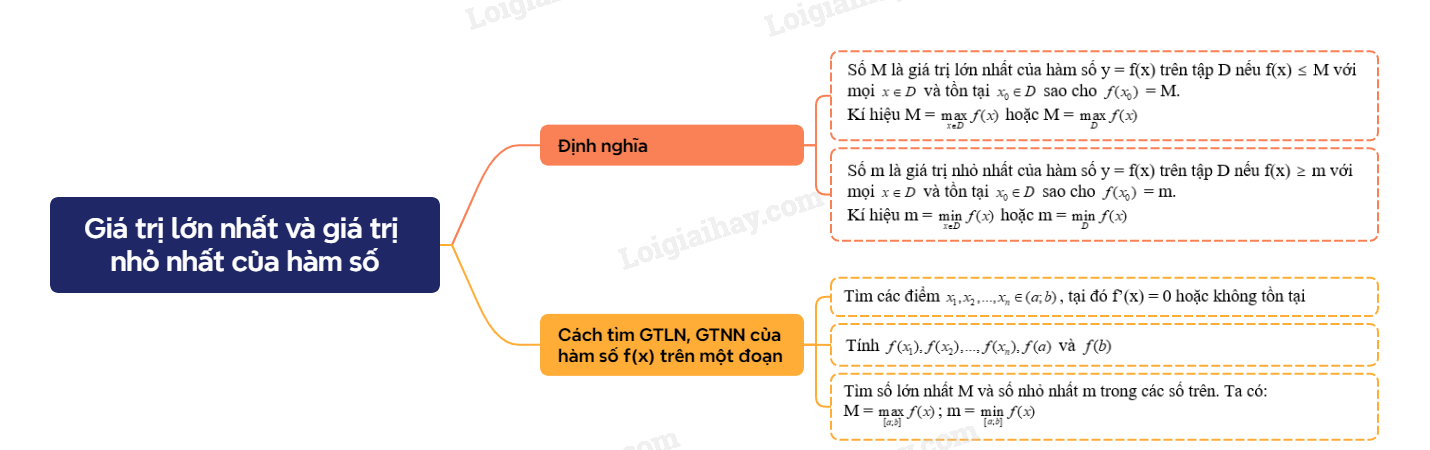
Toán 12 Cánh diều | Giải toán lớp 12 Cánh diều

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cánh Diều

1. Định nghĩa Khái niệm GTLN, GTNN của hàm số

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

1. Định nghĩa

Khái niệm GTLN, GTNN của hàm số

Cho hàm số y = f(x) xác định trên tập D.

- Số M là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) $\le$ M với mọi $x \in D$ và tồn tại ${x_0} \in D$ sao cho $f({x_0})$ = M.

Kí hiệu M = $\mathop {\max }\limits_{x \in D} f(x)$ hoặc M = $\mathop {\max }\limits_D f(x)$

- Số m là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) $\ge$ m với mọi $x \in D$ và tồn tại ${x_0} \in D$ sao cho $f({x_0})$ = m.

Kí hiệu m = $\mathop {\min }\limits_{x \in D} f(x)$ hoặc m = $\mathop {\min }\limits_D f(x)$

2. Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Để tìm GTLN, GTNN của hàm số f(x) trên một khoảng, đoạn hay nửa khoảng, ta có thể lập bảng biến thiên của hàm số trên tập hợp đó. Căn cứ vào bảng biến thiên, ta tìm được GTLN và GTNN (nếu có) của hàm số

Các bước tìm GTLN và GTNN của hàm số f(x) trên đoạn $\left[ {a;b} \right]$ :

Tìm các điểm ${x_1},{x_2},...,{x_n} \in (a;b)$ , tại đó f’(x) = 0 hoặc không tồn tại
Tính $f({x_1}),f({x_2}),...,f({x_n}),f(a)$ và $f(b)$
Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:

M = $\mathop {\max }\limits_{\left[ {a;b} \right]} f(x)$ ; m = $\mathop {\min }\limits_{\left[ {a;b} \right]} f(x)$

Ví dụ: Tìm GTLN và GTNN của hàm số $y = {x^4} - 4{x^2} + 3$ trên đoạn $\left[ {0;4} \right]$

Ta có: $y' = 4{x^3} - 8x = 4x({x^2} - 2);y' = 0 \Leftrightarrow x = 0$ hoặc $x = \sqrt 2$ (vì $x \in \left[ {0;4} \right]$ )

y(0) = 3; y(4) = 195; y( $\sqrt 2$ ) = -1

Do đó: $\mathop {\max }\limits_{\left[ {0;4} \right]} y = y(4) = 195$ ; $\mathop {\min }\limits_{\left[ {0;4} \right]} y = y(\sqrt 2 ) = - 1$

Chia sẻ

Bình luận

Bình chọn:

4.9 trên 7 phiếu

Giải câu hỏi mở đầu trang 15 SGK Toán 12 tập 1 - Cánh diều
Cho một tấm nhôm có dạng hình vuông cạnh 6 dm. Bác Ánh cắt ở bốn góc bốn hình vuông có cùng độ dài cạnh bằng x (dm), rồi gập tấm nhôm lại như Hình 7 để được một cái hộp có dạng hình hộp chữ nhật không có nắp. Gọi V là thể tích của khối hộp đó.
Giải mục 1 trang 15, 16, 17 SGK Toán 12 tập 1 - Cánh diều
Định nghĩa
Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Cánh diều
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bằng đạo hàm
Giải bài tập 1 trang 19 SGK Toán 12 tập 1 - Cánh diều
Nếu hàm số $y = f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ thỏa mãn $f'\left( x \right) = \sin x - 2023,\forall x \in \mathbb{R}$ thì giá trị lớn nhất của hàm số $y = f\left( x \right)$ trên đoạn $\left[ {1;2} \right]$ bằng: A. $f\left( 0 \right)$ . B. $f\left( 1 \right)$ . C. $f\left( {1,5} \right)$ . D. $f\left( 2 \right)$ .
Giải bài tập 2 trang 20 SGK Toán 12 tập 1 - Cánh diều
Tìm giá trị lớn nhất của mỗi hàm số sau: a) (fleft( x right) = frac{4}{{1 + {x^2}}}). b) (fleft( x right) = x - frac{3}{x}) trên nửa khoảng ((0;3]).

Luyện Bài Tập Trắc nghiệm Toán 12 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.