Giải mục 1 trang 15, 16, 17 SGK Toán 12 tập 1 - Cánh diềuĐịnh nghĩa Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Hoá - Sinh - Sử - Địa
Lựa chọn câu để xem lời giải nhanh hơn
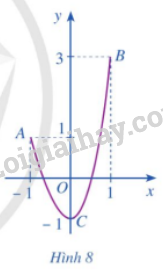
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 15 SGK Toán 12 Cánh diều Cho hàm số y=f(x) liên tục trên đoạn [−1;1] và có đồ thị là đường cong ở Hình 8. Quan sát đồ thị và cho biết: a) Điểm nào thuộc đồ thị hàm số có tung độ lớn nhất b) Điểm nào thuộc đồ thị hàm số có tung độ nhỏ nhất
Lời giải chi tiết: a) Điểm B là điểm thuộc đồ thị hàm số có tung độ lớn nhất b) Điểm C là điểm thuộc đồ thị hàm số có tung độ nhỏ nhất LT1 Trả lời câu hỏi Luyện tập 1 trang 16 SGK Toán 12 Cánh diều Tìm giá trị lớn nhất và nhỏ nhất của hàm số f(x)=√9−x2 trên đoạn [−3;3]. Phương pháp giải: Đánh giá dựa vào điều kiện xác định của x. Lời giải chi tiết: Ta có: x∈[−3;3]⇒0≤x2≤9⇒0≤9−x2≤9⇒0≤√9−x2≤3. Vậy {max[−3;3]f(x)=3⇔x=0min[−3;3]f(x)=0⇔x=±3.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|