Toán 12 Cánh diều | Giải toán lớp 12 Cánh diều

Lý thuyết Đường tiệm cận của đồ thị hàm số Toán 12 Cánh Diều

1. Đường tiệm cận ngang

1. Đường tiệm cận ngang

Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\)

Ví dụ: Tìm TCN của đồ thị hàm số \(y = f(x) = \frac{{3x - 2}}{{x + 1}}\)

Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{3x - 2}}{{x + 1}} = 3\)

Vậy đồ thị hàm số f(x) có TCN là y = 3.

2. Đường tiệm cận đứng

Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \);

Ví dụ: Tìm TCĐ của đồ thị hàm số \(y = f(x) = \frac{{3 - x}}{{x + 2}}\)

Ta có: \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{3x - 2}}{{x + 2}} = + \infty \)

Vậy đồ thị hàm số có TCĐ là x = -2

3.Đường tiệm cận xiên

Đường thẳng \(y = ax + b(a \ne 0)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu

\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\)

Ví dụ: Tìm TCX của đồ thị hàm số \(y = f(x) = x + \frac{1}{{x + 2}}\)

Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 2}} = 0\)

Vậy đồ thị hàm số có TCX là y = x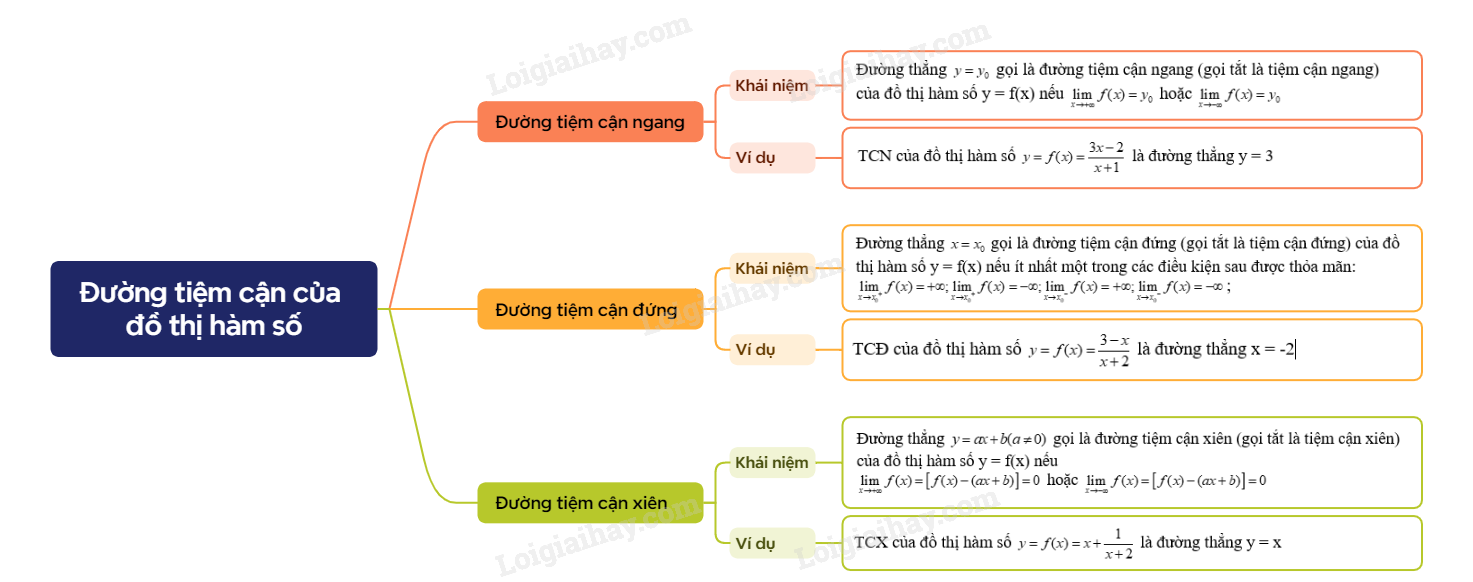