Lý thuyết Biến đổi đơn giản biểu thức chứa căn thức bậc hai Toán 9 Chân trời sáng tạo

1. Trục căn thức ở mẫu

Ví dụ:

\(\frac{2}{{3\sqrt 5 }} = \frac{{2\sqrt 5 }}{{3{{\left( {\sqrt 5 } \right)}^2}}} = \frac{{2\sqrt 5 }}{{3.5}} = \frac{{2\sqrt 5 }}{{15}}\);

\(\frac{a}{{3 - 2\sqrt 2 }} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{\left( {3 - 2\sqrt 2 } \right).\left( {3 + 2\sqrt 2 } \right)}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{{3^2} - {{\left( {2\sqrt 2 } \right)}^2}}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{9 - 8}} = \left( {3 + 2\sqrt 2 } \right)a\).

2. Rút gọn biểu thức chứa căn thức bậc hai

Ví dụ:

\(\begin{array}{l}A = 2\sqrt 3  - \sqrt {75}  + \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}} \\ = 2\sqrt 3  - \sqrt {{{3.5}^2}}  + \left| {1 - \sqrt 3 } \right|\\ = 2\sqrt 3  - 5\sqrt 3  + \sqrt 3  - 1\\ =  - 1 - 2\sqrt 3 \end{array}\)

\(\begin{array}{l}B = x\sqrt x  - \frac{{{x^2} - x}}{{\sqrt x  + 1}}\\ = x\sqrt x  - \frac{{\left( {{x^2} - x} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\\ = x\sqrt x  - \frac{{x\left( {x - 1} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\\ = x\sqrt x  - \frac{{x\left( {x - 1} \right)\left( {\sqrt x  - 1} \right)}}{{x - 1}}\\ = x\sqrt x  - x\left( {\sqrt x  - 1} \right)\\ = x\sqrt x  - x\sqrt x  + x\\ = x\end{array}\)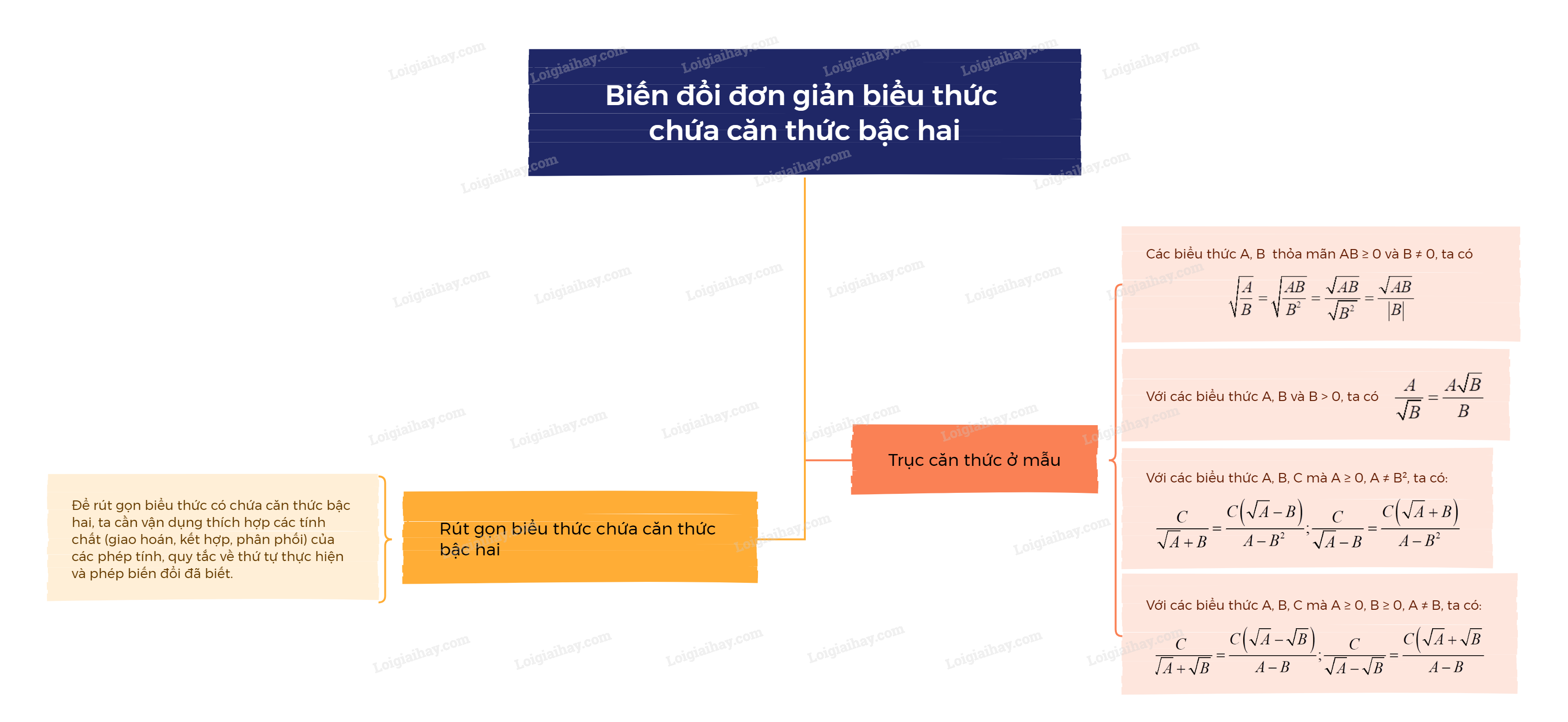