Lý thuyết Bất đẳng thức Toán 9 Cùng khám phá1. Bất đẳng thức Khi so sánh hai số thực a, b bất kì, luôn xảy ra một trong ba trường hợp sau: 1. Bất đẳng thức Khi so sánh hai số thực a, b bất kì, luôn xảy ra một trong ba trường hợp sau: - Số a bằng số b, kí hiệu \(a = b\); - Số a lớn hơn số b, kí hiệu \(a > b\); - Số a nhỏ hơn số b, kí hiệu \(a < b\). Nếu số a không lớn hơn số b thì phải có hoặc \(a < b\), hoặc \(a = b\). Khi đó ta nói gọn là a nhỏ hơn hoặc bằng b và kí hiệu \(a \le b\). Nếu số a không nhỏ hơn số b thì ta phải có hoặc \(a > b\), hoặc \(a = b\). Khi đó, ta nói a lớn hơn hoặc bằng b và kí hiệu \(a \ge b\). Định nghĩa bất đẳng thức
Lưu ý: Bất đẳng thức a > b còn được viết là b < a. Nếu đồng thời có hai bất đẳng thức a > b và a < c thì ta viết gộp lại thành b < a < c (đọc là a lớn hơn b, nhỏ hơn c) Hai bất đẳng thức \(a > b\) và \(c > d\) (hay \(a \ge b\) và \(c \ge d\)) được gọi là hai bất đẳng thức cùng chiều. Hai bất đẳng thức \(a > b\) và \(c < d\) (hay \(a \ge b\) và \(c \le d\)) được gọi là hai bất đẳng thức ngược chiều. 2. Liên hệ giữa thứ tự và phép cộng Với ba số a, b, c, ta có:
Ví dụ: Vì \(2023 < 2024\) nên \(2023 + \left( { - 19} \right) < 2024 + \left( { - 19} \right)\) Lưu ý: Tính chất trên vẫn đúng khi ta trừ vào hai vế của bất đẳng thức với cùng một số. Chẳng hạn, nếu \(a < b\) thì \(a - c < b - c\). Ta có thể sử dụng tính chất trên để so sánh hai số hoặc chứng minh một bất đẳng thức. 3. Liên hệ giữa thứ tự và phép nhân a) Liên hệ giữa thứ tự và phép nhân với số dương
Lưu ý: Tính chất trên vẫn đúng khi ta chia hai vế của bất đẳng thức cho cùng một số dương. Chẳng hạn, nếu \(a < b\) thì \(\frac{a}{c} < \frac{b}{c}\) với c là số dương bất kì. b) Liên hệ giữa thứ tự và phép nhân với số âm
Lưu ý: Tính chất trên vẫn đúng khi ta chia hai vế của bất đẳng thức cho cùng một số âm. Chẳng hạn, nếu \(a < b\) thì \(\frac{a}{c} > \frac{b}{c}\) với c là số âm bất kì. Ví dụ: Vì \( - 7 < - 5\) và \(3 > 0\) nên \(3.\left( { - 7} \right) < 3.\left( { - 5} \right)\). Vì \( - 7 < - 5\) và \( - 3 < 0\) nên \(\left( { - 3} \right).\left( { - 7} \right) > \left( { - 3} \right).\left( { - 5} \right)\). 4. Tính chất bắc cầu của thứ tự
Tính chất bắc cầu cũng đúng với các thứ tự lớn hơn (>), lớn hơn hoặc bằng (\( \ge \)), nhỏ hơn hoặc bằng (\( \le \)). Ví dụ: Vì \(\frac{{2024}}{{2023}} = 1 + \frac{1}{{2023}} > 1\) và \(\frac{{2021}}{{2022}} = 1 - \frac{1}{{2022}} < 1\) nên \(\frac{{2024}}{{2023}} > \frac{{2021}}{{2022}}\). Lưu ý: Các tính chất của thứ tự cũng chính là tính chất của bất đẳng thức. 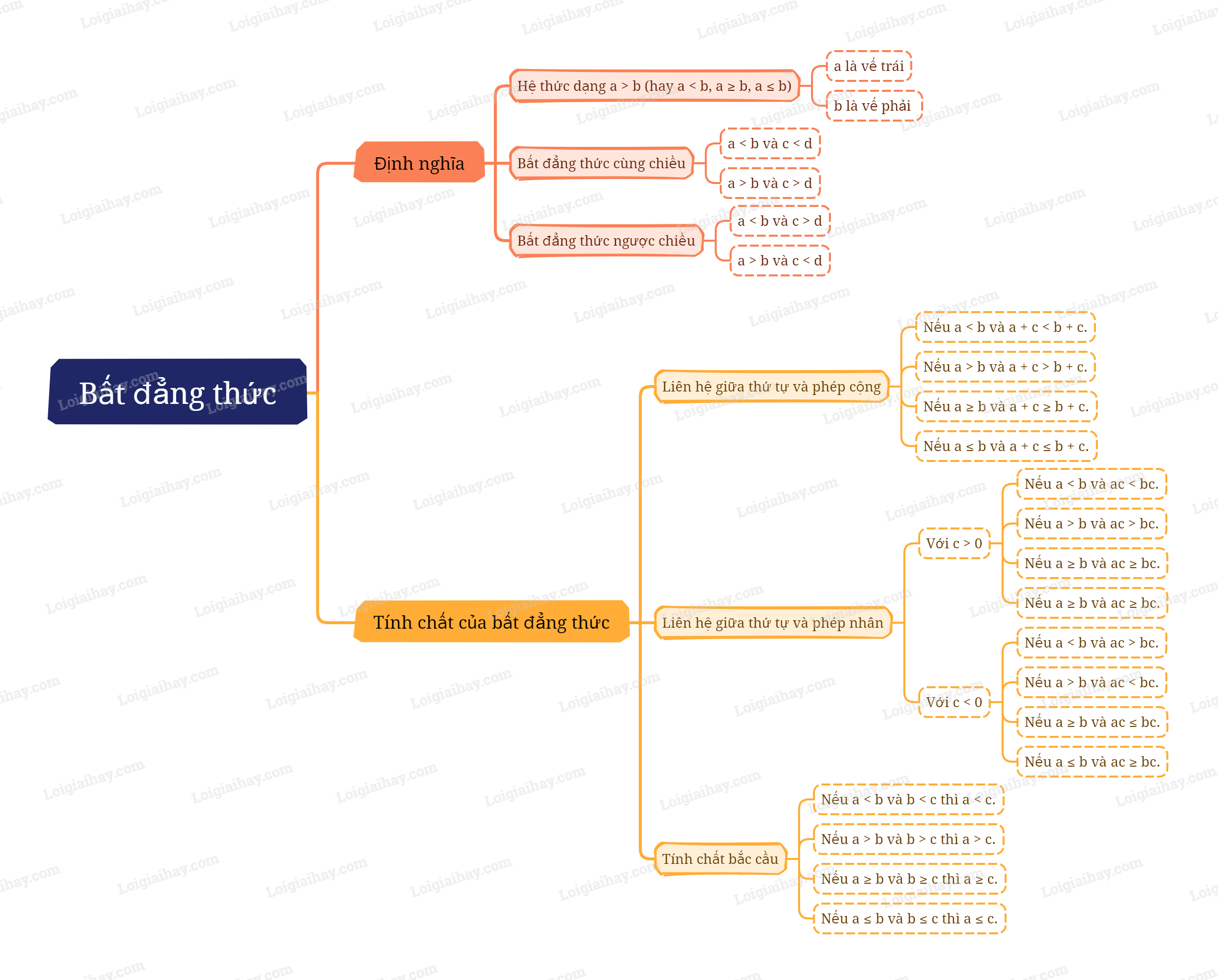
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|



















