Toán lớp 5 Bài 122. Thể tích hình hộp chữ nhật - SGK Bình Minh

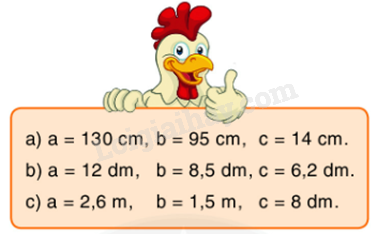
Câu 1

Trả lời câu hỏi 1 trang 50 SGK Toán 5 Bình Minh

Tính thể tích của hình hộp chữ nhật có chiều dài bằng a, chiều rộng bằng b và chiều cao bằng c. Biết:

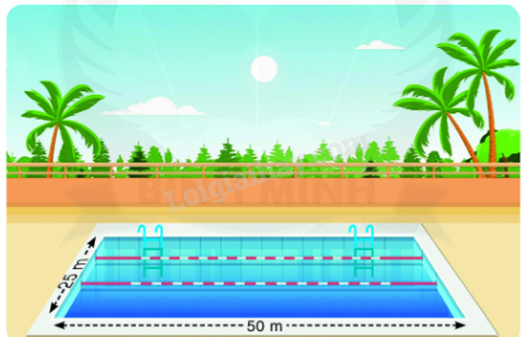
Phương pháp giải:

Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo). $V = a \times b \times c$

Lời giải chi tiết:

a) Thể tích của hình hộp chữ nhật đó là:

\(130 \times 95 \times 14 = 172{\rm{ }}900\)(cm³)

b) Thể tích của hình hộp chữ nhật đó là:

$12 \times 8,5 \times 6,2 = 632,4$(dm³)

c) Đổi: 8dm = 0,8 m

Thể tích của hình hộp chữ nhật đó là:

$2,6 \times 1,5 \times 0,8 = 3,12$(m³)

Câu 2

Trả lời câu hỏi 2 trang 50 SGK Toán 5 Bình Minh

Một bể bơi sâu 1,4 m như hình dưới đây. Hỏi cần bao nhiêu mét khối nước để bơm vào bể bơi đó? Biết rằng mặt nước trong bể cách miệng bể 20 cm.

Phương pháp giải:

- Chiều cao khối nước bơm vào bể = chiều sâu của bể - khoảng cách mặt nước với miệng bể

- Số mét khối nước để bơm vào bể bơi = chiều dài × chiều rộng × chiều cao khối nước bơm vào bể

Lời giải chi tiết:

Đổi 20 cm = 0,2 m

Chiều cao khối nước bơm vào bể là:

1,4 – 0,2 = 1,2 (m)

Số mét khối nước để bơm vào bể bơi là:

$50 \times 25 \times 1,2 = 1500$(m³)

Đáp số: 1 500 m³ nước.

Câu 3

Trả lời câu hỏi 3 trang 50 SGK Toán 5 Bình Minh

Chọn đáp án đúng:

Một thùng đựng hàng dạng hình hộp chữ nhật có chiều dài 2 m, rộng 1,2 m và cao 80 cm. Thể tích của thùng đựng hàng là:

A. 192 m³

B. 256 m³

C. 1,92 m³

D. 19,2 m³

Phương pháp giải:

- Thể tích của thùng đựng hàng = chiều dài × chiều rộng × Chiều cao

Lời giải chi tiết:

Đổi 80 cm = 0,8 m

Thể tích của thùng đựng hàng là:

$2 \times 1,2 \times 0,8 = 1,92$(m³)

Đáp số: 1,92 m³.

Chọn C.