Giải mục 4 trang 30 SGK Toán 12 tập 1 - Cùng khám pháKhảo sát sự biến thiên và vẽ đồ thị của các hàm số sau đây: a) (y = frac{{ - {x^2} - 2x - 2}}{{x + 1}}) b) ({rm{y}} = frac{{{x^2} - 2x - 3}}{{x - 2}})
Lựa chọn câu để xem lời giải nhanh hơn
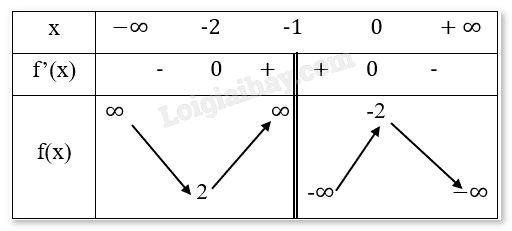
LT3 Trả lời câu hỏi Luyện tập 3 trang 30 SGK Toán 12 Cùng khám phá Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau đây: a) \(y = \frac{{ - {x^2} - 2x - 2}}{{x + 1}}\) b) \({\rm{y}} = \frac{{{x^2} - 2x - 3}}{{x - 2}}\) Phương pháp giải: - Tìm tập xác định của hàm số. - Xét sự biến thiên của hàm số. - Vẽ đồ thị hàm số. Lời giải chi tiết: a) - Tập xác định: D = R \ {-1}. - Sự biến thiên: Giới hạn: \(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = - \infty .\) \(\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {\frac{{ - {{(x + 1)}^2} - 1}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - {1^ - }} \left[ { - (x + 1) - \frac{1}{{x + 1}}} \right] = \infty .\) Suy ra x = -1 là tiệm cận đứng của hàm số. \(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to \infty } [ - (x + 1)] - 0 = - \infty \). \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{ - {x^2} - 2x - 2}}{{x + 1}}} \right) = \mathop {\lim }\limits_{x \to - \infty } [ - (x + 1)] - 0 = \infty \). Suy ra hàm số không có tiệm cận ngang \(\frac{{ - {x^2} - 2x - 2}}{{x + 1}} = - x - 1 + \frac{{ - 1}}{{x + 1}}\) (Sử dụng phép chia đa thức) Khi \(x \to \pm \infty ,\frac{{ - 1}}{{x + 1}} \to 0\) nên \(y = - x - 1\) là tiệm cận xiên của hàm số. Ta có: \({y^\prime } = \frac{{ - (2x + 2)(x + 1) + \left( {{x^2} + 2x + 2} \right)}}{{{{(x + 1)}^2}}} = \frac{{ - {x^2} - 2x}}{{{{(x + 1)}^2}}}\). \({y^\prime } = 0 \leftrightarrow - {x^2} - 2x \leftrightarrow - x(x + 2) = 0 \leftrightarrow x = 0,{\rm{ }}x = - 2\). Bảng biến thiên:
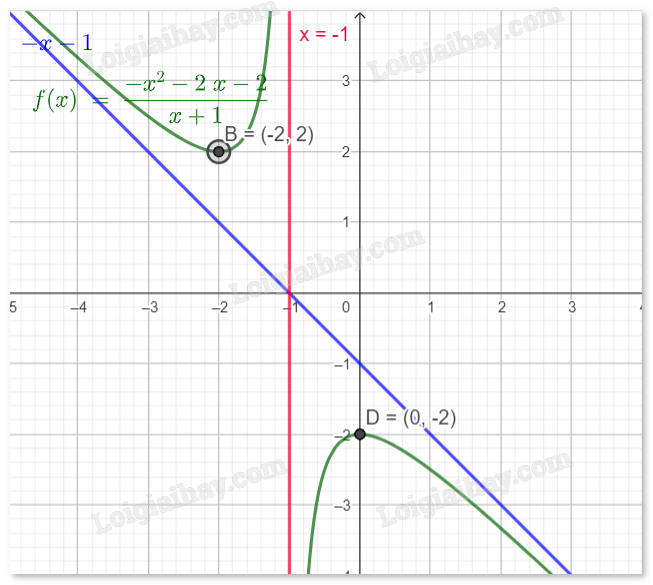
Chiều biến thiên: Hàm số nghịch biến trên các khoảng (−∞,-2) và (-1,0), đồng biến trên khoảng (-2,-1) và (-1,0). Cực trị: Hàm số đạt cực tiểu tại \(x = - 2,{y_{CT}} = 2\). Hàm số đạt cực đại tại \(x = 0,{y_{CD}} = - 2\). - Vẽ đồ thị: Tiệm cận đứng \({\rm{x}} = - 1\), tiệm cận xiên \(y = - x - 1\). Giao điểm với trục Oy là \((0, - 2)\).
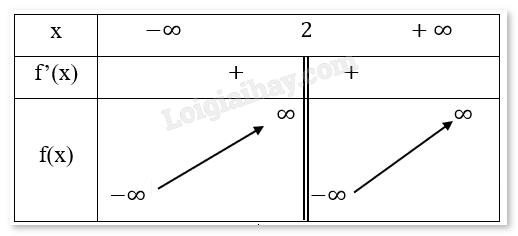
b) - Tập xác định: D = R \ {2}. - Sự biến thiên: Giới hạn: \(\mathop {\lim }\limits_{x \to 2 + } y = \mathop {\lim }\limits_{x \to 2 + } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \). \(\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \). Suy ra x = 2 là tiệm cận đứng của hàm số. \(\mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = \infty \). \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{{x^2} - 2x - 3}}{{x - 2}}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\frac{{(x - 3)(x + 1)}}{{x - 2}}} \right) = - \infty \). Suy ra hàm số không có tiệm cận ngang \(\frac{{{x^2} - 2x - 3}}{{x - 2}} = x + \frac{{ - 3}}{{x + 1}}\) . Khi \(x \to \pm \infty ,\frac{{ - 3}}{{x + 1}} \to 0\) nên \(y = x\) là tiệm cận xiên của hàm số. Ta có: \({y^\prime } = \frac{{(2x - 2)(x - 2) - \left( {{x^2} - 2x - 3} \right)}}{{{{(x - 2)}^2}}} = \frac{{{x^2} - 4x + 7}}{{{{(x - 2)}^2}}} > 0\forall x \in D\). Vậy hàm số đồng biến trên tập xác định. Bảng biến thiên:
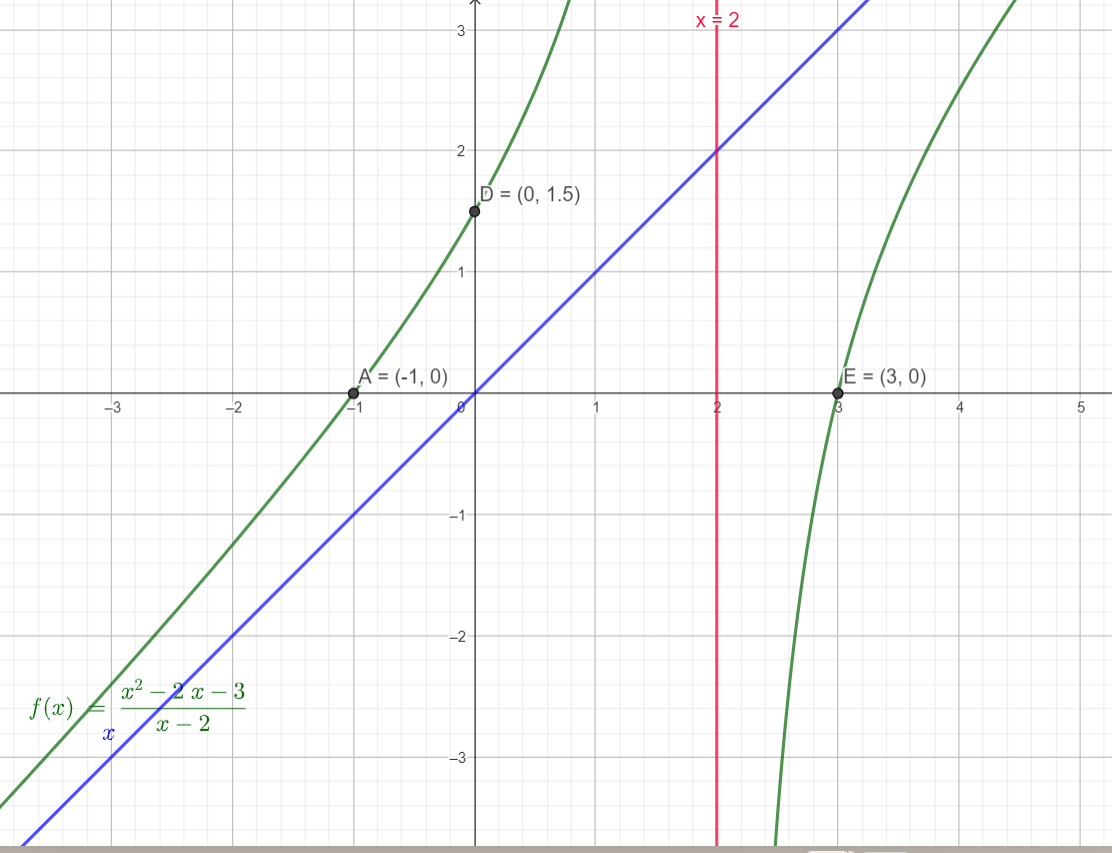
Chiều biến thiên: Hàm số đồng biến trên khoảng (-\(\infty ,2\)) và (2, \(\infty \)). Cực trị: Hàm số không có cực trị. - Vẽ đồ thị: Tiệm cận đứng x = 2, tiệm cận xiên y = x. Giao điểm với trục Oy là (0,\(\frac{3}{2}\)). Giao điểm với trục Ox là (-1,0) và (3,0).
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|