Giải mục 3 trang 47, 48, 49 SGK Toán 12 tập 2 - Cùng khám pháTrong không gian \(Oxyz\), cho hai mặt phẳng \(\left( {{\alpha _1}} \right):2x - 3y + z + 3 = 0\), \(\left( {{\alpha _2}} \right):4x - 6y + 2z + 5 = 0\)và điểm \(M( - 2;0;1)\). a) Hãy chỉ ra một vectơ pháp tuyến của mỗi mặt phẳng. Có nhận xét gì về phương của các vectơ này? b) Mặt phẳng nào đi qua điểm M? c) Hai mặt phẳng này song song với nhau không? Vì sao?
Lựa chọn câu để xem lời giải nhanh hơn
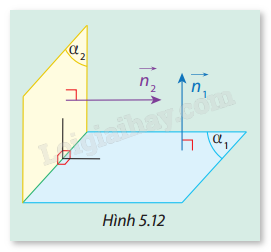
HĐ6 Trả lời câu hỏi Hoạt động 6 trang 47 SGK Toán 12 Cùng khám phá Trong không gian \(Oxyz\), cho hai mặt phẳng \(\left( {{\alpha _1}} \right):2x - 3y + z + 3 = 0\), \(\left( {{\alpha _2}} \right):4x - 6y + 2z + 5 = 0\)và điểm \(M( - 2;0;1)\). a) Hãy chỉ ra một vectơ pháp tuyến của mỗi mặt phẳng. Có nhận xét gì về phương của các vectơ này? b) Mặt phẳng nào đi qua điểm M? c) Hai mặt phẳng này song song với nhau không? Vì sao? Phương pháp giải: a) Phương trình mặt phẳng có dạng \(Ax + By + Cz + D = 0\) thì \(\overrightarrow n = \left( {A;B;C} \right)\) chính là vectơ pháp tuyến của mặt phẳng đó. b) Thay \(M\) vào từng phương trình của mặt phẳng để kiểm tra. c) Nếu vectơ pháp tuyến của hai mặt phẳng song song hoặc trùng nhau thì hai mặt phẳng đó cũng song song hoặc trùng nhau. Lời giải chi tiết: a) Vectơ pháp tuyến của hai mặt phẳng là: \(\overrightarrow {{n_{{\alpha _1}}}} = \left( {2; - 3;1} \right)\), \(\overrightarrow {{n_{{\alpha _2}}}} = \left( {4; - 6;2} \right)\) Có thể thấy hai vectơ này cùng phương với nhau vì: \(\frac{4}{2} = \frac{{ - 6}}{{ - 3}} = \frac{2}{1} = 2\) b) Thay M vào phương trình mặt phẳng \(({\alpha _1})\): \(2.( - 2) - 3.0 + 1 + 3 = 0\) Thay M vào phương trình mặt phẳng \(({\alpha _2})\): \(4.( - 2) - 6.0 + 2.1 + 5 = - 1 \ne 0\) Vậy M thuộc mặt phẳng \(({\alpha _1})\) nhưng không thuộc mặt phẳng \(({\alpha _2})\). c) Từ câu a có thể thấy hai vectơ pháp tuyến \(\overrightarrow {{n_{{\alpha _1}}}} ,\overrightarrow {{n_{{\alpha _2}}}} \) song song với nhau nên hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) có thể song song hoặc trùng nhau. Mặt khác, điểm M thuộc mặt phẳng \(({\alpha _1})\) nhưng không thuộc mặt phẳng \(({\alpha _2})\) nên hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) song song với nhau. LT7 Trả lời câu hỏi Luyện tập 7 trang 48 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, cho hình lăng trụ \(ABC.A'B'C'\) với các điểm \(A'(3;2; - 5)\), \(A(3;1; - 1)\), \(B(2; - 1;4)\), và \(C(0;2;1)\). a) Chứng minh rằng mặt phẳng (ABC) song song với mặt phẳng \(\alpha \): \(9x + 13y + 7z = 0\) b) Viết phương trình mặt phẳng (A'B'C'). Phương pháp giải: a) - Tìm vectơ pháp tuyến của mặt phẳng (ABC). - Sử dụng tính chất: Hai mặt phẳng song song khi và chỉ khi các vector pháp tuyến của chúng cùng phương, nghĩa là tỉ số các hệ số của hai phương trình mặt phẳng phải tương ứng với nhau. b) - Vectơ pháp tuyến của mặt phẳng A′B′C′ cũng là vectơ pháp tuyến của mặt phẳng ABC vì hai mặt phẳng này song song. - Sau đó viết phương trình mặt phẳng dựa vào vectơ pháp tuyến này và tọa độ của một điểm trên mặt phẳng, ví dụ A′. Lời giải chi tiết: a) Tọa độ các điểm \(A(3;1; - 1)\), \(B(2; - 1;4)\), \(C(0;2;1)\). Vector \(\overrightarrow {AB} = B - A = (2 - 3, - 1 - 1,4 - ( - 1)) = ( - 1, - 2,5)\). Vector \(\overrightarrow {AC} = C - A = (0 - 3,2 - 1,1 - ( - 1)) = ( - 3,1,2)\). Tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là: \(\overrightarrow {{n_{ABC}}} = \overrightarrow {AB} \times \overrightarrow {AC} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\{ - 1}&{ - 2}&5\\{ - 3}&1&2\end{array}} \right| = {\bf{i}} \cdot (( - 2) \cdot 2 - 5 \cdot 1) - {\bf{j}} \cdot (( - 1) \cdot 2 - 5 \cdot ( - 3)) + {\bf{k}} \cdot (( - 1) \cdot 1 - ( - 2) \cdot ( - 3))\) \( = {\bf{i}} \cdot ( - 4 - 5) - {\bf{j}} \cdot ( - 2 + 15) + {\bf{k}} \cdot ( - 1 - 6) = {\bf{i}} \cdot ( - 9) - {\bf{j}} \cdot (13) + {\bf{k}} \cdot ( - 7) = ( - 9, - 13, - 7).\) Vậy vector pháp tuyến của mặt phẳng (ABC) là \(\overrightarrow {{n_{ABC}}} = ( - 9, - 13, - 7)\). Phương trình mặt phẳng \(\alpha \) cho trước là: \(9x + 13y + 7z = 0\). Vector pháp tuyến của mặt phẳng \(\alpha \) là \(\overrightarrow {{n_\alpha }} = (9,13,7)\). Ta thấy \(\overrightarrow {{n_{ABC}}} = ( - 9, - 13, - 7)\) là cùng phương với \(\overrightarrow {{n_\alpha }} \), do đó hai mặt phẳng (ABC) và \(\alpha \) song song với nhau. b) Vì \(ABC.A'B'C'\) là hình lăng trụ nên mặt phẳng ABC và mặt phẳng A′B′C′ song song với nhau nên vectơ pháp tuyến của mặt phẳng ABC cũng là vectơ pháp tuyến của mặt phẳng A′B′C′. Suy ra vector pháp tuyến của mặt phẳng A′B′C′ là \(\overrightarrow {{n_{A'B'C'}}} = ( - 9, - 13, - 7)\). Phương trình mặt phẳng (A'B'C') là: \( - 9(x - 3) - 13(y - 2) - 7(z + 5) = 0\) hay rút gọn lại là: \( - 9x - 13y - 7z + 18 = 0\) HĐ7 Trả lời câu hỏi Hoạt động 7 trang 48 SGK Toán 12 Cùng khám phá Cho hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) có vectơ pháp tuyến tương ứng là \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) (Hình 5.12). a) Có nhận xét gì về góc giữa \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) khi \(({\alpha _1}) \bot ({\alpha _2})\)? b) Nếu \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) vuông góc với nhau thì \(({\alpha _1})\) và \(({\alpha _2})\) có vuông góc với nhau không? Vì sao?
Phương pháp giải: a) Góc giữa hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) cũng là góc giữa hai vectơ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \). b) Tương tự thì góc góc giữa hai vectơ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) cũng là góc giữa hai mặt phẳng \(({\alpha _1})\) và. Lời giải chi tiết: a) Khi hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) vuông góc, điều này có nghĩa rằng góc giữa hai mặt phẳng bằng \({90^\circ }\). Do đó, vectơ pháp tuyến \(\overrightarrow {{n_1}} \) của mặt phẳng \(({\alpha _1})\) và vectơ pháp tuyến \(\overrightarrow {{n_2}} \) của mặt phẳng \(({\alpha _2})\) cũng sẽ vuông góc với nhau. Điều này được biểu diễn bằng tích vô hướng của hai vectơ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \): \(\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} = 0.\) Kết luận: Khi \(({\alpha _1}) \bot ({\alpha _2})\), thì \(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \). b) Nếu \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) vuông góc với nhau, tức là \(\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} = 0\), thì hai mặt phẳng \(({\alpha _1})\) và \(({\alpha _2})\) cũng sẽ vuông góc với nhau vì: \(\left( {{\alpha _1}} \right) \bot \overrightarrow {{n_1}} ,\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \to \left( {{\alpha _1}} \right)//\overrightarrow {{n_2}} \) Mà \(\left( {{\alpha _2}} \right) \bot \overrightarrow {{n_2}} \to \left( {{\alpha _1}} \right) \bot \left( {{\alpha _2}} \right)\). LT8 Trả lời câu hỏi Luyện tập 8 trang 49 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, cho hình chóp S.ABC có \(S(2; - 1;7)\), \(A(2; - 1;3)\), \(B(5;2;3)\), \(C(8; - 1;3)\). Chứng minh rằng mặt phẳng (SAB) vuông góc với hai mặt phẳng (ABC) và (SBC). Phương pháp giải: Để chứng minh mặt phẳng \((SAB)\) vuông góc với mặt phẳng \((ABC)\), ta cần kiểm tra xem tích vô hướng của hai vectơ pháp tuyến của hai mặt phẳng này có bằng 0 hay không. - Tương tự, để chứng minh mặt phẳng \((SAB)\) vuông góc với mặt phẳng \((SBC)\), ta cũng kiểm tra điều kiện tích vô hướng giữa hai vectơ pháp tuyến của chúng. Lời giải chi tiết: * Tìm vectơ pháp tuyến của các mặt phẳng a) Mặt phẳng \((ABC)\): - Ta cần tìm hai vectơ chỉ phương của mặt phẳng \((ABC)\): \(\overrightarrow {AB} = B - A = (5 - 2;2 + 1;3 - 3) = (3;3;0),\) \(\overrightarrow {AC} = C - A = (8 - 2; - 1 + 1;3 - 3) = (6;0;0).\) - Vectơ pháp tuyến của mặt phẳng \((ABC)\) là tích có hướng của \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \): \(\overrightarrow {{n_{ABC}}} = \overrightarrow {AB} \times \overrightarrow {AC} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\3&3&0\\6&0&0\end{array}} \right| = (0;0; - 18).\) Do đó, một vectơ pháp tuyến của mặt phẳng \((ABC)\) là \(\overrightarrow {{n_{ABC}}} = (0;0; - 18)\). b) Mặt phẳng \((SAB)\): - Ta cần tìm hai vectơ chỉ phương của mặt phẳng \((SAB)\): \(\overrightarrow {SA} = A - S = (2 - 2; - 1 + 1;3 - 7) = (0;0; - 4),\) \(\overrightarrow {SB} = B - S = (5 - 2;2 + 1;3 - 7) = (3;3; - 4).\) - Vectơ pháp tuyến của mặt phẳng \((SAB)\) là tích có hướng của \(\overrightarrow {SA} \) và \(\overrightarrow {SB} \): \(\overrightarrow {{n_{SAB}}} = \overrightarrow {SA} \times \overrightarrow {SB} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\0&0&{ - 4}\\3&3&{ - 4}\end{array}} \right| = (12; - 12;0).\) Do đó, một vectơ pháp tuyến của mặt phẳng \((SAB)\) là \(\overrightarrow {{n_{SAB}}} = (12; - 12;0)\). c) Mặt phẳng \((SBC)\): - Tương tự, ta cần tìm hai vectơ chỉ phương của mặt phẳng \((SBC)\): \(\overrightarrow {SB} = (3;3; - 4)\quad {\rm{v\`a }}\quad \overrightarrow {SC} = C - S = (8 - 2; - 1 + 1;3 - 7) = (6;0; - 4).\) - Vectơ pháp tuyến của mặt phẳng \((SBC)\) là tích có hướng của \(\overrightarrow {SB} \) và \(\overrightarrow {SC} \): \(\overrightarrow {{n_{SBC}}} = \overrightarrow {SB} \times \overrightarrow {SC} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\3&3&{ - 4}\\6&0&{ - 4}\end{array}} \right| = ( - 12; - 12; - 18).\) Do đó, một vectơ pháp tuyến của mặt phẳng \((SBC)\) là: \(\overrightarrow {{n_{SBC}}} = ( - 12; - 12; - 18)\) * Chứng minh các mặt phẳng vuông góc a) Mặt phẳng \((SAB)\) và \((ABC)\): - Để kiểm tra \((SAB)\) vuông góc với \((ABC)\), ta tính tích vô hướng của \(\overrightarrow {{n_{SAB}}} \) và \(\overrightarrow {{n_{ABC}}} \): \(\overrightarrow {{n_{SAB}}} \cdot \overrightarrow {{n_{ABC}}} = (12; - 12;0) \cdot (0;0; - 18) = 12 \times 0 + ( - 12) \times 0 + 0 \times ( - 18) = 0.\) - Vì tích vô hướng bằng 0, nên \((SAB) \bot (ABC)\). b) Mặt phẳng \((SAB)\) và \((SBC)\): - Tương tự, ta tính tích vô hướng của \(\overrightarrow {{n_{SAB}}} \) và \(\overrightarrow {{n_{SBC}}} \): \(\overrightarrow {{n_{SAB}}} \cdot \overrightarrow {{n_{SBC}}} = (12; - 12;0) \cdot ( - 12; - 12; - 18) = 12 \times ( - 12) + ( - 12) \times ( - 12) + 0 \times ( - 18) = - 144 + 144 + 0 = 0.\) - Vì tích vô hướng bằng 0, nên \((SAB) \bot (SBC)\). LT9 Trả lời câu hỏi Luyện tập 9 trang 49 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, viết phương trình mặt phẳng \((\alpha )\) đi qua \(A( - 3;2; - 1)\) và vuông góc với hai mặt phẳng \((P):2x - y + 3z - 1 = 0\), \((Q):x + 2y - 2z + 3 = 0\). Phương pháp giải: - Vectơ pháp tuyến của mặt phẳng \((\alpha )\) phải vuông góc với cả hai vectơ pháp tuyến của các mặt phẳng \((P)\) và \((Q)\). - Từ đó, ta tìm vectơ pháp tuyến của \((\alpha )\) bằng tích có hướng của hai vectơ pháp tuyến của \((P)\) và \((Q)\). - Sau khi có vectơ pháp tuyến của \((\alpha )\), sử dụng điểm \(A( - 3;2; - 1)\) để lập phương trình mặt phẳng \((\alpha )\). Lời giải chi tiết: - Vectơ pháp tuyến của mặt phẳng \((P)\) là: \(\overrightarrow {{n_P}} = (2; - 1;3).\) - Vectơ pháp tuyến của mặt phẳng \((Q)\) là: \(\overrightarrow {{n_Q}} = (1;2; - 2).\) - Vectơ pháp tuyến của mặt phẳng \((\alpha )\) phải vuông góc với cả hai vectơ \(\overrightarrow {{n_P}} \) và \(\overrightarrow {{n_Q}} \), do đó ta tìm tích có hướng của hai vectơ này: \(\overrightarrow {{n_\alpha }} = \overrightarrow {{n_P}} \times \overrightarrow {{n_Q}} = \left| {\begin{array}{*{20}{c}}{\bf{i}}&{\bf{j}}&{\bf{k}}\\2&{ - 1}&3\\1&2&{ - 2}\end{array}} \right| = {\bf{i}}\left| {\begin{array}{*{20}{c}}{ - 1}&3\\2&{ - 2}\end{array}} \right| - {\bf{j}}\left| {\begin{array}{*{20}{c}}2&3\\1&{ - 2}\end{array}} \right| + {\bf{k}}\left| {\begin{array}{*{20}{c}}2&{ - 1}\\1&2\end{array}} \right|\) Tính các định thức con: \(\overrightarrow {{n_\alpha }} = {\bf{i}} \cdot (( - 1)( - 2) - (3)(2)) - {\bf{j}} \cdot ((2)( - 2) - (3)(1)) + {\bf{k}} \cdot ((2)(2) - ( - 1)(1))\) \( = {\bf{i}} \cdot (2 - 6) - {\bf{j}} \cdot ( - 4 - 3) + {\bf{k}} \cdot (4 + 1)\) \( = {\bf{i}} \cdot ( - 4) - {\bf{j}} \cdot ( - 7) + {\bf{k}} \cdot (5)\) \( = ( - 4;7;5).\) Vậy vectơ pháp tuyến của mặt phẳng \((\alpha )\) là \(\overrightarrow {{n_\alpha }} = ( - 4;7;5)\). - Phương trình tổng quát của mặt phẳng \((\alpha )\) có dạng: \( - 4(x + 3) + 7(y - 2) + 5(z + 1) = 0.\) - Ta thế tọa độ điểm \(A( - 3;2; - 1)\) vào phương trình: \( - 4(x + 3) + 7(y - 2) + 5(z + 1) = 0.\) Mở rộng phương trình: \( - 4x - 12 + 7y - 14 + 5z + 5 = 0\) \( - 4x + 7y + 5z - 21 = 0.\) Vậy phương trình của mặt phẳng \((\alpha )\) là: \( - 4x + 7y + 5z - 21 = 0.\)
|