Giải mục 2 trang 97, 98, 99 SGK Toán 9 tập 2 - Kết nối tri thứcNêu một số đồ vật có dạng hình nón trong đời sống. Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh
Lựa chọn câu để xem lời giải nhanh hơn
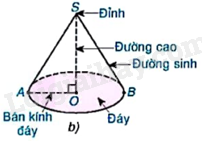
CH Video hướng dẫn giải Trả lời câu hỏi Câu hỏi trang 97 SGK Toán 9 Kết nối tri thức Nêu một số đồ vật có dạng hình nón trong đời sống. Phương pháp giải: Hình nón có dạng:
Lời giải chi tiết: Một số đồ vật có dạng hình nón trong cuộc sống:
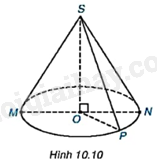
LT3 Video hướng dẫn giải Trả lời câu hỏi Luyện tập 3 trang 98 SGK Toán 9 Kết nối tri thức Kể tên các bán kính đáy và đường sinh còn lại của hình nón trong Hình 10.10.
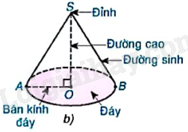
Phương pháp giải: Hình nón có dạng:
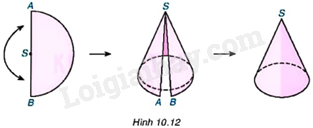
Lời giải chi tiết: ON, OP là các bán kính đáy của hình nón. SP, SN là các đường sinh của hình nón. TH2 Video hướng dẫn giải Trả lời câu hỏi Thực hành 2 trang 98 SGK Toán 9 Kết nối tri thức Cắt một nửa hình tròn bằng giấy cứng, đường kính và tâm là S. Cuộn nửa hình tròn đó lại sao cho SA và SB sát vào nhau như Hình 10.12 (dùng băng keo dán), ta được một hình nón đỉnh S. Hãy cho biết độ dài đường sinh và chu vi đáy của hình nón đó.
Phương pháp giải: Độ dài đường sinh chính là đoạn thẳng SA. Chu vi đáy của hình nón chính là nửa chu vi hình tròn đường kính AB. Lời giải chi tiết: Ta có đường sinh của hình nón là đoạn thẳng SA nên độ dài đường sinh là (cm). Vì hình nón được tạo bởi nửa hình tròn nên chu vi đáy của hình nón chính là độ dài cung AB hay nửa chu vi của hình tròn đường kính AB. Chu vi hình tròn đáy của hình nón là: (cm). HĐ3 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 3 trang 98 SGK Toán 9 Kết nối tri thức Người ta coi diện tích hình quạt SAB (xem Thực hành 2) chính là diện tích xung quanh của hình nón được tạo thành. Cho hình nón có đường sinh và bán kính đáy . Tính diện tích mặt xung quanh của hình nón. Phương pháp giải: Sử dụng công thức tính diện tích hình quạt tròn có độ dài cung tròn l và bán kính R là: Lời giải chi tiết: Vì bán kính đáy của hình nón là r = 5cm nên ta có độ dài cung AB chính là chu vi của hình tròn bán kính 5cm. Do đó độ dài cung AB là:
Diện tích hình quạt có độ dài cung tròn là và bán kính R là 9 là:
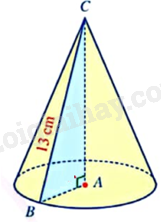
Vậy diện tích mặt xung quanh của hình nón là . HĐ4 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 4 trang 99 SGK Toán 9 Kết nối tri thức Hãy nhắc lại công thức tính thể tích của hình chóp tam giác đều (hoặc hình chóp tứ giác đều) có diện tích đáy S và chiều cao h. Phương pháp giải: Nhớ lại công thức tính thể tích hình chóp tam giác đều (tứ giác đều) đã học ở lớp 8. Lời giải chi tiết: Thể tích của hình chóp tam giác đều (hoặc hình chóp tứ giác đều) có diện tích đáy S và chiều cao h là . LT4 Video hướng dẫn giải Trả lời câu hỏi Luyện tập 4 trang 99 SGK Toán 9 Kết nối tri thức Tính diện tích xung quanh và thể tích của một hình nón có độ dài đường sinh bằng 13cm và chiều cao bằng 12cm. Phương pháp giải: Diện tích xung quanh của hình nón bán kính r và độ dài đường sinh l là: . Thể tích của hình nón bán kính r và chiều cao h là: . Lời giải chi tiết:
Xét hình nón có đường sinh và chiều cao . Tam giác CAB vuông tại A nên
Diện tích xung quanh của hình nón là: . Thể tích của hình nón là: . VD Video hướng dẫn giải Trả lời câu hỏi Vận dụng trang 99 SGK Toán 9 Kết nối tri thức Người ta đổ muối thu hoạch được trên cánh đồng muối thành từng đống có dạng hình nón với chiều cao khoảng 0,9m và đường kính đáy khoảng 1,6m. Hỏi mỗi đống muối có bao nhiêu đềximét khối muối (làm tròn kết quả đến hàng đơn vị).
Phương pháp giải: Thể tích của hình nón bán kính r và chiều cao h là: . Lời giải chi tiết: Bán kính đống muối là: . Mỗi đống muối có số đềximét khối là:
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|