Giải mục 2 trang 68,69,70 SGK Toán 12 tập 1 - Cánh diềuTọa độ của một vecto Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Hoá - Sinh - Sử - Địa
Lựa chọn câu để xem lời giải nhanh hơn
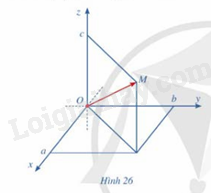
HĐ3 Trả lời câu hỏi Hoạt động 3 trang 68 SGK Toán 12 Cánh diều Cho điểm M trong không gian với hệ tọa độ Oxyz a) Vẽ vecto →OM b) Nêu cách xác định tọa độ của điểm M Lời giải chi tiết: a)
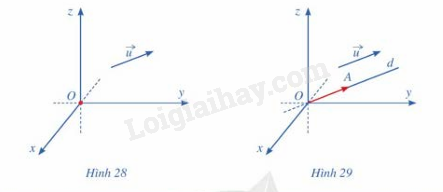
b) Nếu →OM có tọa độ (a;b;c) thì ta viết →OM = (a;b;c), trong đó a là hoành độ, b là tung độ và c là cao độ HĐ4 Trả lời câu hỏi Hoạt động 4 trang 69 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, cho vecto →u(hình 28). Hãy xác định điểm A sao cho →OA=→u
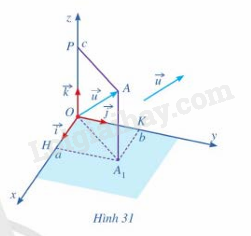
Phương pháp giải: Vẽ →OAcó tung độ, hoành độ và cao độ giống nhau Lời giải chi tiết: →OA=→u khi cả hai có chung tung độ hoành độ và cao độ bằng nhau HĐ5 Trả lời câu hỏi Hoạt động 5 trang 70 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, cho vecto →u=(a;b;c)( hình 31) Lấy điểm A sao cho →OA=→u. a) Tìm hoành độ, tung độ và cao độ của điểm A b) Biểu diễn vecto →OH qua vecto→i vecto →OK qua vecto →j ,vecto →OPqua vecto →k c) Biểu diễn vecto →utheo các vecto →i,→j,→k
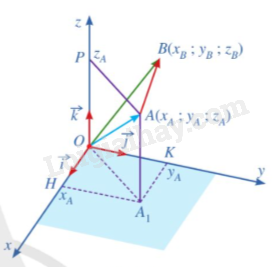
Phương pháp giải: Áp dụng quy tắc các tọa độ của vecto Lời giải chi tiết: a)Ox là hoành độ của điểm A Oy là tung dộ của điểm A Oz là cao độ của điểm A b)→OH=→ai →OK=→jb →OP=→kc c) →u=→OA=→OH+→OK => →u=→ai+→bj HĐ6 Trả lời câu hỏi Hoạt động 6 trang 71 SGK Toán 12 Cánh diều Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(xA;yA;zA),B(xB;yB;zB) a.Biểu diễn mỗi vecto →OA,→OB theo các vecto →i,→j và →k b. Tìm liên hệ giữa →AB và (xB−xA).→i+(yB−yA).→j+(zB−zA).→k c. Từ đó, tìm tọa độ vecto →AB Phương pháp giải: Sử dụng lý thuyết tọa độ của vecto trong không gian Lời giải chi tiết: a) →OA=→OA1+→OP=→OH+→OK=xA.→i+yA.→j+zA.→k Tương tự, ta có: →OB=xB.→i+yB.→j+zB.→k b) Ta có: →AB=→OB−→OA=xB.→i+yB.→j+zB.→k−(xA.→i+yA.→j+zA.→k)=(xB−xA).→i+(yB−yA).→j+(zB−zA).→k c)Tọa độ vecto →AB(xB−xA;yB−yA;zB−zA)
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|