Giải mục 2 trang 47, 48, 49 SGK Toán 9 tập 1 - Chân trời sáng tạoThực hiện các phép tính cho trên bảng trong Hình 1. b) Từ đó, có nhận xét gì về căn bậc hai của tích hai số không âm? Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Lựa chọn câu để xem lời giải nhanh hơn
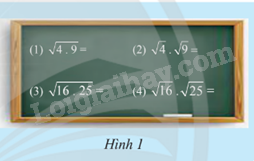
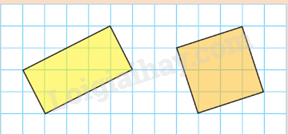
HĐ2 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 2 trang 47 SGK Toán 9 Chân trời sáng tạo a) Thực hiện các phép tính cho trên bảng trong Hình 1. b) Từ đó, có nhận xét gì về căn bậc hai của tích hai số không âm? Phương pháp giải: Dựa vào và . ( a > 0) Lời giải chi tiết: a) (1) (2) (3) (4) b) Căn bậc hai của tích hai số không âm bằng tích các căn bậc hai của hai số không âm. HĐ3 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 3 trang 48 SGK Toán 9 Chân trời sáng tạo Thay mỗi ? bằng các số thích hợp: a) b) c) d) Phương pháp giải: Dựa vào tính chất với a, b > 0 Lời giải chi tiết: a) b) c) d) TH3 Video hướng dẫn giải Trả lời câu hỏi Thực hành 3 trang 49 SGK Toán 9 Chân trời sáng tạo Tính a) b) c) d) e) Phương pháp giải: Dựa vào tính chất với a, b > 0 Lời giải chi tiết: a) b) c) d) e) TH4 Video hướng dẫn giải Trả lời câu hỏi Thực hành 4 trang 49 SGK Toán 9 Chân trời sáng tạo Rút gọn các biểu thức sau: a) b) với a 0 c) với a > 2 Phương pháp giải: Dựa vào tính chất với a, b > 0 Lời giải chi tiết: a) b) c) TH5 Video hướng dẫn giải Trả lời câu hỏi Thực hành 5 trang 49 SGK Toán 9 Chân trời sáng tạo Đưa thừa số vào trong dấu căn bậc hai: a) b) c) với a > 0 Phương pháp giải: Dựa vào tính chất với a, b > 0 Lời giải chi tiết: a) b) c) . VD1 Video hướng dẫn giải Trả lời câu hỏi Vận dụng 1 trang 49 SGK Toán 9 Chân trời sáng tạo Tính diện tích của hình chữ nhật và hình vuông trong hoạt động khởi động. Biết mỗi ô vuông nhỏ có độ dài cạnh là 1. Diện tích của hai hình đó bằng nhau không?
Phương pháp giải: Dựa vào công thức tính diện tích hình chữ nhật và hình vuông. Lời giải chi tiết: Độ dài chiều dài hình chữ nhật là: Độ dài chiều rộng hình chữ nhật là: Diện tích hình chữ nhật là: Độ dài cạnh hình vuông là: Diện tích hình vuông là: Vậy diện tích hai hình bằng nhau.
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|