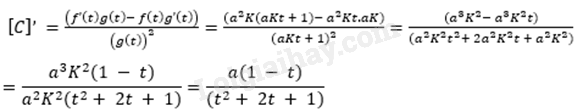Giải bài tập 8 trang 44 SGK Toán 12 tập 1 - Cánh diềuXét phản ứng hoá học tạo ra chất C từ hai chất A và B: \(A{\rm{ }} + {\rm{ }}B{\rm{ }} \to {\rm{ }}C\) Giả sử nồng độ của hai chất A và B bằng nhau [A] = [B] = a (mol/l). Khi đó, nồng độ của chất C theo thời gian t (t > 0) được cho bởi công thức: \(\left[ C \right]\; = \;\frac{{{a^2}Kt}}{{aKt + 1}}\) (mol/l), trong đó K là hằng số dương. a) Tìm tốc độ phản ứng ở thời điểm t > 0. b) Chứng minh nếu \(x\; = \;\left[ C \right]\) thì c) Nêu hiện tượng xảy ra với nồng độ các chất khi \(t\; \to \ Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Hoá - Sinh - Sử - Địa Đề bài
Xét phản ứng hoá học tạo ra chất C từ hai chất A và B: \(A{\rm{ }} + {\rm{ }}B{\rm{ }} \to {\rm{ }}C\) Giả sử nồng độ của hai chất A và B bằng nhau [A] = [B] = a (mol/l). Khi đó, nồng độ của chất C theo thời gian t (t > 0) được cho bởi công thức: \(\left[ C \right]\; = \;\frac{{{a^2}Kt}}{{aKt + 1}}\) (mol/l), trong đó K là hằng số dương. a) Tìm tốc độ phản ứng ở thời điểm t > 0. b) Chứng minh nếu \(x\; = \;\left[ C \right]\) thì c) Nêu hiện tượng xảy ra với nồng độ các chất khi \(t\; \to \; + \infty \) d) Nêu hiện tượng xảy ra với tốc độ phản ứng khi \(t\; \to \; + \infty \) Phương pháp giải - Xem chi tiết
Lời giải chi tiết a) Tốc độ phản ứng được xác định bằng đạo hàm của nồng độ chất C theo thời gian t. Vì vậy, ta cần tính đạo hàm của hàm số [C] \( = \frac{{{a^2}Kt}}{{aKt + 1}}\) theo thời gian t. Đặt \(f\left( t \right)\; = {a^2}Kt\) và \(g\left( t \right)\; = aKt + 1\). Khi đó, [C] \( = \frac{{f\left( t \right)}}{{g\left( t \right)}}.\) Ta có: Đạo hàm của \(f\left( t \right)\) theo t: $f\left( t \right)~={{a}^{2}}K$. Đạo hàm của \(g\left( t \right)\) theo t:$g\left( t \right)~=aK$ Ta có:
Vậy, tốc độ phản ứng ở thời điểm t > 0 là: (Mol/(l.s)) b) Để chứng minh điều này, ta cần chứng minh rằng đạo hàm của \(x\; = \;\left[ C \right]\) theo thời gian t, x’(t), bằng với Ta đã tính được từ phần trước. Giả sử . Thay \(x{\rm{\;}} = {\rm{\;}}\left[ C \right] = \frac{{{{\rm{a}}^2}{\rm{Kt}}}}{{{\rm{aKt}} + 1}}\) vào phương trình ta có: $x\left( t \right)=~K{{\left( \frac{a-\left( {{a}^{2}}Kt \right)}{aKt+1} \right)}^{2}}=~K{{\left( a\left( \frac{1-aKt}{aKt+1} \right) \right)}^{2}}=~K{{\left( a\left( \frac{1-t}{t+\frac{1}{a}} \right) \right)}^{2}}=~K{{\left( a\left( \frac{1}{t+\frac{1}{a}} \right) \right)}^{2}}=~K{{\left( \frac{a}{t+\frac{1}{a}} \right)}^{2}}=~K{{\left( \frac{a}{t+a} \right)}^{2}}=~K{{\left( \frac{a\left( 1~-~t \right)}{\left( {{t}^{2}}+~2t~+~1 \right)} \right)}^{2}}$ So sánh với ta thấy hai biểu thức này chỉ bằng nhau khi \({\rm{K\;}} = \frac{1}{{\rm{a}}}\) Vậy, nếu \({\rm{K\;}} = \frac{1}{{\rm{a}}}\;\)thì c) Đối với chất A và B, do chúng liên tục phản ứng để tạo ra chất C, nên nồng độ của chúng sẽ giảm dần và khi \(t\; \to \; + \infty \), nồng độ của chúng sẽ tiến tới 0. Đối với chất C, ta có \(\left[ C \right] = \frac{{{a^2}Kt}}{{aKt + 1}}\). Khi \(t\; \to \; + \infty \), ta có: \(\left[ C \right] = \frac{{{a^2}Kt}}{{aKt + 1}} = \frac{{{a^2}}}{{\left( {a\; + \frac{1}{t}} \right)}}\) → a (mol/l) Vậy, khi \(t\; \to \; + \infty \), nồng độ của chất C sẽ tiến tới a. d) Tốc độ phản ứng được cho bởi công thức: . Khi \(t\; \to \; + \infty \), ta có: .$x\left( t \right)=~\frac{a\left( 1~-~t \right)}{\left( {{t}^{2}}+~2t~+~1 \right)}~\to 0$. Vậy, khi thời gian t tiến tới vô cùng, tốc độ phản ứng sẽ giảm dần và tiến tới 0. Điều này cho thấy phản ứng đã hoàn toàn xảy ra, và không còn chất nào tiếp tục phản ứng nữa.
|