Giải bài tập 6 trang 43 SGK Toán 12 tập 1 - Cánh diều

Đề bài

 

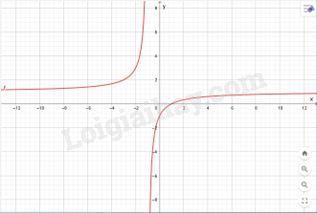
Khảo sát sự biến thiên của các hàm số sau:

a, $y = \frac{{x - 1}}{{x + 1}}$

b,$y = \frac{{ - 2x}}{{x + 1}}$

c,$y=\frac{{{x^2} - 3x + 6}}{{x - 1}}$

d,$y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}$

e,$y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}$

g,$y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}$

Lời giải chi tiết

a) $y = \frac{{x - 1}}{{x + 1}}$

1) TXĐ: $x \in \mathbb{R}\left\{ { - 1} \right\}$

2) Sự biến thiên

$y' = \frac{2}{{{{\left( {x + 1} \right)}^2}}} > 0\;$ với mọi $x \ne  - 1$

Bảng biến thiên:

Hàm số đồng biến trên khoảng $\left( { - \infty ; - 1} \right)$ và $\left( { - 1; + \infty } \right)$

Hàm số không có cực trị

3) Đồ thị

Giao điểm đồ thị với trục tung: $\left( {0; - 1} \right)$

Giao điểm đồ thị với trục hoành: $\left( {1;0} \right)$

Đồ thị đi qua các điểm: $\left( {0; - 1} \right)$, $\left( {1;0} \right)$

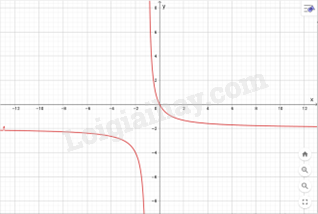
b) $y = \frac{{ - 2x}}{{x + 1}}$

1) TXĐ: $x \in \mathbb{R}\backslash \left\{ { - 1} \right\}$

2) Sự biến thiên

 với mọi $x \ne  - 1$

Bảng biến thiên:

Hàm số nghịch biến trên khoảng $\left( { - \infty , - 1} \right) \cup \left( { - 1,\infty } \right)$

3) Đồ thị

Giao điểm đồ thị với trục tung: $\left( {0;0} \right)$

Giao điểm đồ thị với trục hoành: $\left( {0;0} \right)$

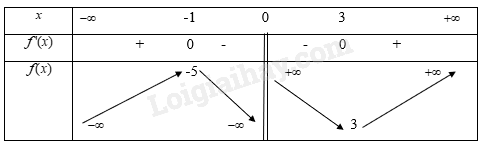
c) $y = \frac{{{x^2} - 3x + 6}}{{x - 1}}$

1) TXĐ: $x \in \mathbb{R}\backslash \left\{ 1 \right\}$

2) Sự biến thiên

Ta có $y = \frac{{{x^2} - 3x + 6}}{{x - 1}}$$= x - 2 + \frac{4}{{x - 1}}$

$y' = 1 - \frac{4}{{{{(x - 1)}^2}}}$$= \frac{{{x^2} - 2x - 3}}{{{{(x - 1)}^2}}}$

Xét $y' = 0$$\Rightarrow \left[ \begin{array}{l}x = 3\\x =  - 1\end{array} \right.$

Bảng biến thiên

Hàm số đồng biến trên khoảng $\left( { - \infty , - 1} \right),\left( {3, + \infty } \right)$. Nghịch biến trên khoảng $\left( { - 1,1} \right),\left( {1,3} \right)$

3) Đồ thị

Giao điểm đồ thị với trục tung: $\left( {0; - 6} \right)$

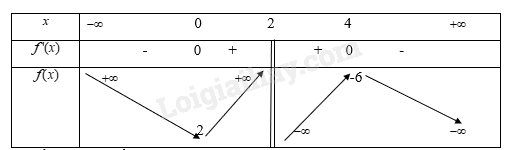
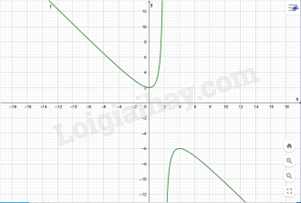
d) $y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}$

Hàm số trên xác định trên R\{2}

Ta có $y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}$$=  - x - \frac{4}{{x - 2}}$

          $y' =  - 1 + \frac{4}{{{{(x - 2)}^2}}}$$= \frac{{ - {x^2} + 4x}}{{{{(x - 2)}^2}}}$

Xét $y' = 0$$\Rightarrow \left[ \begin{array}{l}x = 0\\x = 4\end{array} \right.$

Từ đó ta có bảng biến thiên là

Từ bảng biến thiên ta thấy

Hàm số đồng biến $y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}$trên các khoảng $(0;2)$ và $(2;4)$

Hàm số nghịch biến $y = \frac{{ - {x^2} + 2x - 4}}{{x - 2}}$trên các khoảng $( - \infty ;0)$ và $(4; + \infty )$

Ta có đồ thị hàm số là

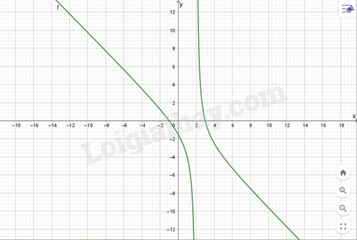
e) $y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}$

Hàm số xác định trên R\{-2}

Ta có $y = \frac{{2{x^2} + 3x - 5}}{{x + 2}}$ $= 2x - \frac{{x + 5}}{{x + 2}}$

           $y' = 2 + \frac{3}{{{{(x + 2)}^2}}}$

Vì $y' > 0$với $x \in R/\left\{ { - 2} \right\}$

Nên hàm số luôn đồng biến với $x \in R/\left\{ { - 2} \right\}$

Ta có đồ thị hàm số là

g) $y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}$

Hàm số xác định trên R/{2}

Ta có : $y = \frac{{{x^2} - 2x - 3}}{{ - x + 2}}$ $=  - x + \frac{3}{{x - 2}}$

           $y' =  - 1 - \frac{3}{{{{(x - 2)}^2}}}$

Vì $y' < 0$với $x \in R/\left\{ 2 \right\}$

Nên hàm số luôn nghịch biến với $x \in R/\left\{ 2 \right\}$

Ta có đồ thị hàm số là