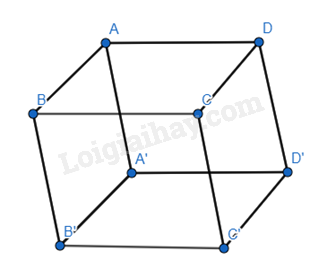
Giải bài tập 7 trang 81 SGK Toán 12 tập 1 - Cánh diềuCho hình hộp ABCD.A’B’C’D’, biết A(1;0;1), B(2;1;2), D(1;-1;1), C’(4;5;-5). Hãy chỉ ra tọa độ của một vecto khác (overrightarrow 0 ) vuông góc với cả hai vecto trong mỗi trường hợp sau: a) (overrightarrow {AC} ) và (overrightarrow {B'D'} ) b) (overrightarrow {AC'} ) và (overrightarrow {BD} ) Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Đề bài Cho hình hộp ABCD.A’B’C’D’, biết A(1;0;1), B(2;1;2), D(1;-1;1), C’(4;5;-5). Hãy chỉ ra tọa độ của một vecto khác \(\overrightarrow 0 \) vuông góc với cả hai vecto trong mỗi trường hợp sau: a) \(\overrightarrow {AC} \) và \(\overrightarrow {B'D'} \) b) \(\overrightarrow {AC'} \) và \(\overrightarrow {BD} \) Phương pháp giải - Xem chi tiết Cho hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\) không cùng phương. Khi đó, vecto \(\overrightarrow w = ({y_1}{z_2} - {y_2}{z_1};{z_1}{x_2} - {z_2}{x_1};{x_1}{y_2} - {x_2}{y_1})\) vuông góc với cả hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) Lời giải chi tiết
a) Ta có: \(\overrightarrow {AB} = (1;1;1),\overrightarrow {AD} = (0; - 1;0)\) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {AC} = (1;0;1\)) \(\overrightarrow {B'D'} = \overrightarrow {BD} = ( - 1; - 2; -1 )\) \([\overrightarrow {AC} ,\overrightarrow {B'D'} ] = \left( {\left| \begin{array}{l}\;\;\;0\;\;\;\;1\\ - 2\;\;\;\;\;1\end{array} \right|;\left| \begin{array}{l}1\;\;\;\;\;\;1\\\;-1\;\;\;\;\; - 1\end{array} \right|;\left| \begin{array}{l}1\;\;\;\;\;\;\;0\\ - 1\;\;\;\; - 2\end{array} \right|} \right) = (2; 0;- 2)\) Chọn \(\overrightarrow u = (2; 0; - 2)\) vuông góc với cả hai vecto \(\overrightarrow {AC} \) và \(\overrightarrow {B'D'} \). b) \(\overrightarrow {AC'} = (3;5; - 6)\), \(\overrightarrow {BD} = ( - 1; - 2; - 1)\) \([\overrightarrow {AC'} ,\overrightarrow {BD} ] = \left( {\left| \begin{array}{l}\;\;\;5\;\;\;\; - 6\\ - 2\;\;\;\;\; - 1\end{array} \right|;\left| \begin{array}{l} - 6\;\;\;\;\;\;3\\\; - 1\;\;\;\;\; - 1\end{array} \right|;\left| \begin{array}{l}3\;\;\;\;\;\;\;5\\ - 1\;\;\;\; - 2\end{array} \right|} \right) = ( - 17;9; - 1)\) Chọn \(\overrightarrow v = ( - 17;9; - 1)\) vuông góc với cả hai vecto \(\overrightarrow {AC'} \) và \(\overrightarrow {BD} \).
|