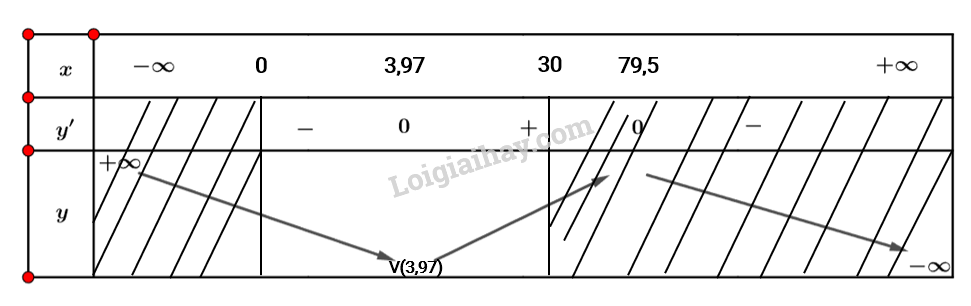
Giải bài tập 6 trang 14 SGK Toán 12 tập 1 - Cánh diềuThể tích V (đơn vị: centimet khối) của 1kg nước tại nhiệt độ T\(\left( {0{{\rm{ }}^o}C \le T \le 30{{\rm{ }}^o}C} \right)\) được tính bởi công thức sau: \(V\left( T \right) = 999,87 - 0,06426T + 0,0085043{T^2} - 0,0000679{T^3}\). Hỏi thể tích \(V\left( T \right)\),\(\left( {0{{\rm{ }}^o}C \le T \le 30{{\rm{ }}^o}C} \right)\) giảm trong khoảng nhiệt độ nào? Đề bài Thể tích V (đơn vị: centimet khối) của 1kg nước tại nhiệt độ T\(\left( {0{{\rm{ }}^o}C \le T \le 30{{\rm{ }}^o}C} \right)\) được tính bởi công thức sau: \(V\left( T \right) = 999,87 - 0,06426T + 0,0085043{T^2} - 0,0000679{T^3}\). Hỏi thể tích \(V\left( T \right)\),\(\left( {0{{\rm{ }}^o}C \le T \le 30{{\rm{ }}^o}C} \right)\) giảm trong khoảng nhiệt độ nào? Phương pháp giải - Xem chi tiết B1: Tìm tập xác định của hàm số. B2: Tính đạo hàm. Tìm các điểm mà tại đó đạo hàm bằng không hoặc không tồn tại. B3: Lập bảng biến thiên. B4: Dựa vào bảng biến thiên để kết luận. Lời giải chi tiết Tập xác định: \(D = \mathbb{R}\). Ta có: \(V'\left( T \right) = - 0,06426 + 2 \times 0,0085043 \times T - 3 \times 0,0000679{T^2}\). Nhận xét \(V'\left( T \right) = 0 \Leftrightarrow \left[ \begin{array}{l}T \approx 79,5\\T \approx 3,97\end{array} \right.\). Ta có bảng biến thiên sau:
Vậy thể tích giảm trong khoảng nhiệt độ từ \(\left( {{0^o};3,{{97}^o}} \right)\).  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
