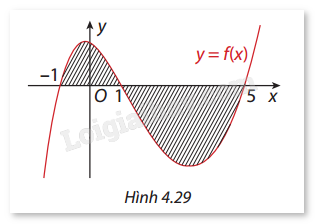
Giải bài tập 4.38 trang 38 SGK Toán 12 tập 2 - Cùng khám pháCho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\). Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f(x),y = 0,x = - 1\) và \(x = 5\) (Hình 4.29). Mệnh đề nào sau đây dúng? Đề bài Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\). Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f(x),y = 0,x = - 1\) và \(x = 5\) (Hình 4.29). Mệnh đề nào sau đây dúng?
A. \(S = - \int_1^1 f (x)dx - \int_1^5 f (x)dx\) B. \(S = \int_1^1 f (x)dx + \int_1^5 f (x)dx\) C. \(S = \int_1^1 f (x)dx\quad \int_1^5 f (x)dx\) D. \(S = - \int_{ - 1}^1 f (x)dx + \int_1^5 f (x)dx\) Phương pháp giải - Xem chi tiết Diện tích hình phẳng được xác định bằng tích phân của giá trị tuyệt đối của hàm số trên đoạn đã cho. Để tính diện tích, cần xem xét khoảng nào hàm số nằm phía dưới trục hoành và khoảng nào nằm phía trên trục hoành. Lời giải chi tiết Xét hình phẳng trong hình vẽ, hàm \(f(x)\) có phần nằm trên trục hoành (dương) từ \(x = - 1\) đến \(x = 1\), và phần nằm dưới trục hoành (âm) từ \(x = 1\) đến \(x = 5\). - Với khoảng \(x = - 1\) dếdn \(x = 1\), \(f(x) > 0\)nên diện tích sẽ là \(\int_{ - 1}^1 f (x)dx\). - Với khoảng \(x = 1\) đến \(x = 5\), \(f(x) < 0\) nên diện tích sẽ là \( - \int_1^5 f (x)dx\). Tổng diện tích là: \(S = \int_{ - 1}^1 f (x)dx - \int_1^5 f (x)dx\) Chọn C.
|