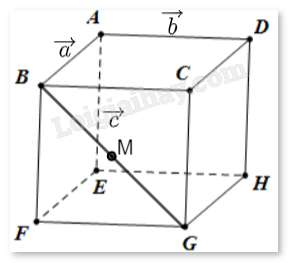
Giải bài tập 2.4 trang 64 SGK Toán 12 tập 1 - Cùng khám phá

Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G, G' lần lượt là trọng tâm các tam giác ABC và A'B'C'. O là giao điểm của hai đường thẳng AB' và A'B. a) Chứng minh rằng các đường thẳng GO và CG' song song với nhau. b) Tính độ dài của \(\overrightarrow {GO} \)trong trường hợp ABC.A'B'C' là hình lăng trụ đứng, cạnh bên AA' = 3 và đáy là tam giác đều có cạnh bằng 2.

Trọng lực \(\vec P\) là lực hấp dẫn do Trái Đất tác dụng lên một vật được tính bởi công thức \(\vec P = m\vec g\), trong đó \(m\) là khối lượng của vật (đơn vị: kg), \(\vec g\) là vectơ gia tốc rơi tự do, có hướng đi xuống và có độ lớn \(g = 9,8{\mkern 1mu} {\rm{m/}}{{\rm{s}}^2}\). Xác định hướng và độ lớn của trọng lực (đơn vị: N) tác dụng lên quả bóng có khối lượng 450 gam.

Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính: a) \(\overrightarrow {BC} .\overrightarrow {AH} ;\) b) \(\overrightarrow {AF} .\overrightarrow {EG} ;\) c) \(\overrightarrow {AC} .\overrightarrow {FE} .\)

Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng a và (widehat {BAA'} = widehat {BAD} = widehat {DAA'} = {60^circ }). Tính độ dài đường chéo AC’.

Cho tứ diện ABCD. Hai điểm M và N theo thứ tự là trung điểm của BC và AD. Cho biết AB = 10, CD = 6, MN = 7. a) Chứng minh rằng (overrightarrow {NM} = frac{1}{2}left( {overrightarrow {AB} + overrightarrow {DC} } right)). b) Từ kết quả câu a, hãy tính (overrightarrow {AB} .overrightarrow {DC} ). c) Tính (left( {overrightarrow {AB} ,overrightarrow {DC} } right)).