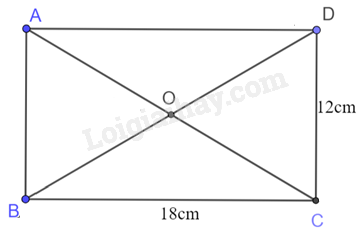
Giải bài tập 2 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạoCho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó. Đề bài Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó. Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Đọc kĩ dữ liệu đề bài để vẽ hình - Áp dụng khoảng cách từ tâm đến đường tròn để chứng minh 4 điểm thuộc đường tròn - Bán kính đường tròn bằng nửa đường chéo hình chữ nhật. Lời giải chi tiết
Ta có ABCD là hình chữ nhật và gọi O là giao của hai đường chéo AC và BD. Nên ta có OA = OB = OC = OD suy ra bốn điểm A, B, C, D cùng thuộc đường tròn tâm O, bán kính OA. Áp dụng định lí Pythagore vào tam giác vuông ACD, ta có: \(AC = \sqrt {AD^2 + CD^2} = \sqrt {18^2 + 12^2} = 6\sqrt {13}\) Suy ra R = OA = \(\frac{{AC}}{2} = \frac{{6\sqrt {13}}}{2} = 3\sqrt {13}cm\).  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
