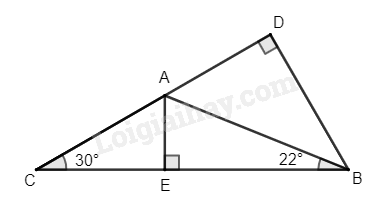
Giải bài tập 2 trang 71 SGK Toán 9 tập 1 - Chân trời sáng tạo

Đề bài

Cho tam giác ABC có BC = 20 cm, $\widehat {ABC} = {22^o},\widehat {ACB} = {30^o}$

a) Tính khoảng cách từ điểm B đến đường thẳng AC.

b) Tính các cạnh và các góc còn lại của tam giác ABC.

c) Tính khoảng cách từ điểm A đến đường thẳng BC.

Lời giải chi tiết

a) Gọi BD là đường cao hạ từ B xuống AC.

Xét tam giác BDC, $\widehat {ACB} = {30^o}$ ta có:

$BD = \sin \widehat {ACB}.BC = \sin {30^o}.20 = 10cm$

Vậy khoảng cách từ điểm B đến đường thẳng AC chính là BD = 10 cm.

b) Xét tam giác ABC, ta có:

$\widehat {CAB} = {180^o} - \widehat {ACB} - \widehat {ABC} = {180^o} - {30^o} - {22^o} = {128^o}$

Xét tam giác ABD vuông tại D, $\widehat {CAB} = {128^o}$ nên $\widehat {DAB} = {180^o - 128^o = 52^o}$, ta có:

$AB = \frac{{BD}}{{\sin \widehat {DAB}}} \approx 12,7$cm

Áp dụng định lý Pythagore, ta có:

$AD = \sqrt {A{B^2} - B{D^2}}  = \sqrt {{{12.7}^2} - {{10}^2}}  \approx 7,8cm$

Xét tam giác BCD vuông tại D, $\widehat {ACB} = {30^o}$ ta có:

$CD = \frac{{BD}}{{\tan \widehat {ACB}}} \approx 17,3$cm

Suy ra $AC = CD - AD \approx 17,3 - 7,8 = 9,5 cm$.

c) Gọi AE là đường cao hạ từ A xuống BC.

Xét tam giác ACE vuông tại E, $\widehat {ACB} = {30^o}$, ta có:

$AE =  AC.sin\widehat {ACB} = 9,5.sin 30^o \approx 4,8 cm.$

Vậy khoảng cách từ điểm A đến đường thẳng BC khoảng 4,8 cm.