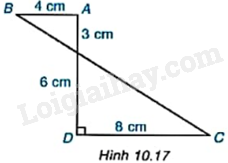
Giải bài tập 10.6 trang 100 SGK Toán 9 tập 2 - Kết nối tri thứcTính thể tích của hình tạo thành khi cho hình ABCD quanh AD một vòng (H.10.17). Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Tính thể tích của hình tạo thành khi cho hình ABCD quanh AD một vòng (H.10.17).
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Khi quay hình ABCD quanh cạnh AD một vòng thì ta được một hình gồm hai hình nón có: + Hình nón thứ nhất có chiều cao bằng 3cm, bán kính đáy bằng 4cm. + Hình nón thứ hai có chiều cao bằng 6cm, bán kính đáy bằng 8cm. Thể tích của hình nón bán kính r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\). Lời giải chi tiết Khi quay hình ABCD quanh cạnh AD một vòng thì ta được một hình gồm hai hình nón có: + Hình nón thứ nhất có chiều cao bằng 3cm, bán kính đáy bằng 4cm. + Hình nón thứ hai có chiều cao bằng 6cm, bán kính đáy bằng 8cm. Thể tích hình nón thứ nhất là: \({V_1} = \frac{1}{3}\pi {.4^2}.3 = 16\pi \left( {c{m^3}} \right)\). Thể tích hình nón thứ hai là: \({V_2} = \frac{1}{3}\pi {.8^2}.6 = 128\pi \left( {c{m^3}} \right)\). Thể tích hình cần tìm là: \(V = {V_1} + {V_2} = 16\pi + 128\pi = 144\pi \left( {c{m^3}} \right)\).  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
