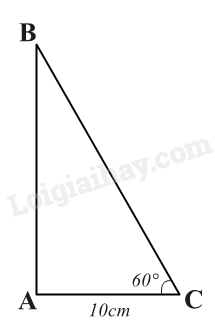
Giải bài tập 1 trang 72 SGK Toán 9 tập 1 - Chân trời sáng tạo

Đề bài

Cho tam giác ABC vuông tại A có AC = 10 cm, $\widehat C = {60^o}$. Độ dài hai cạnh còn lại là:

A. $AB = \frac{{5\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm$

B. $AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{14\sqrt 3 }}{3}cm$

C. $AB = 10\sqrt 3 cm;BC = 20cm$

D. $AB = \frac{{10\sqrt 3 }}{3}cm;BC = \frac{{20\sqrt 3 }}{3}cm$

Lời giải chi tiết

Xét tam giác ABC vuông tại A, $\widehat C = {60^o}$, ta có:

$AB = tan\widehat C. AC = tan{60^o}. 10 = 10\sqrt 3$ cm

$BC = \frac{{AB}}{{\sin \widehat C}} = \frac{{10\sqrt 3}}{{\sin {{60}^o}}} = 20$cm.

Chọn đáp án C.