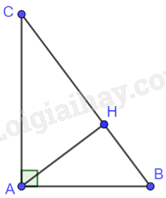
Giải bài 9.46 trang 63 sách bài tập toán 8 - Kết nối tri thức với cuộc sống

Đề bài

Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng $AB = 6cm$ và $AC = 8cm$, hãy tính độ dài các đoạn thẳng BC, AH, BH, CH.

Lời giải chi tiết

Tam giác ABC vuông tại A nên $\widehat {BAC} = {90^0}$

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có: $B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100$ nên $BC = 10cm$

Vì AH là đường cao trong tam giác ABC nên $AH \bot BC$.

Do đó, $\widehat {AHB} = \widehat {AHC} = {90^0}$

Tam giác ABC và tam giác HAC có: $\widehat {BAC} = \widehat {AHC} = {90^0},\widehat C$ chung. Do đó, $\Delta ABC\backsim \Delta HAC\left( g-g \right)$

Suy ra: $\frac{{AC}}{{HC}} = \frac{{BC}}{{AC}}$ nên $CH = \frac{{C{A^2}}}{{CB}} = \frac{{{8^2}}}{{10}} = \frac{{32}}{5}\left( {cm} \right)$

Do đó, $BH = BC - CH = 10 - \frac{{32}}{5} = \frac{{18}}{5}\left( {cm} \right)$

Vì $\Delta ABC\backsim \Delta HAC\left( cmt \right)$ nên $\frac{{AB}}{{HA}} = \frac{{BC}}{{AC}}$

Do đó, $AH = \frac{{AB.AC}}{{BC}} = \frac{{6.8}}{{10}} = \frac{{24}}{5}\left( {cm} \right)$