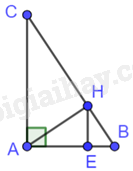
Giải bài 9.45 trang 63 sách bài tập toán 8 - Kết nối tri thức với cuộc sống

Đề bài

Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ đường thẳng HE vuông góc với AB (E thuộc AB). Chứng minh rằng:

a) $\Delta ABC\backsim \Delta HAC$ và $C{A^2} = CH.CB$

b) $\frac{{AH}}{{BC}} = \frac{{HE}}{{AB}}$

Lời giải chi tiết

Tam giác ABC vuông tại A nên $\widehat {BAC} = {90^0}$

Vì AH là đường cao trong tam giác ABC nên $AH \bot BC$.

Do đó, $\widehat {AHB} = \widehat {AHC} = {90^0}$

Tam giác ABC và tam giác HAC có: $\widehat {BAC} = \widehat {AHC} = {90^0},\widehat C$ chung

Do đó, $\Delta ABC\backsim \Delta HAC\left( g-g \right)$

Suy ra: $\frac{{AC}}{{HC}} = \frac{{BC}}{{AC}}$ nên $C{A^2} = CH.CB$

b) Vì HE vuông góc với AB (E thuộc AB) nên $\widehat {AEH} = {90^0}$

Tam giác AHE và tam giác CBA có:

$\widehat {AEH} = \widehat {BAC} = {90^0},\widehat {HAE} = \widehat C$ (cùng phụ với góc CAH)

Do đó, $\Delta AHE\backsim \Delta CBA\left( g-g \right)$. Suy ra $\frac{{AH}}{{BC}} = \frac{{HE}}{{AB}}$