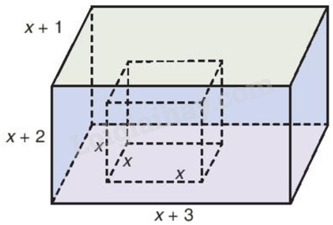
Giải bài 7 trang 107 vở thực hành Toán 7 tập 2Người ta đổ đầy nước vào một cái bể hình hộp chữ nhật, sau đó nhấn chìm một khối lập phương (đặc) có độ dài các cạnh bằng x(dm) vào trong bể. Biết rằng chiều rộng, chiều dài và chiều cao của bể lần lượt bằng (x + 1,x + 3) và (x + 2) (xem dưới đây). a) Tìm đa thức biểu thị lượng nước còn lại trong bể. b) Xác định bậc, hệ số cao nhất và hệ số tự do của đa thức trong câu a. c) Sử dụng kết quả câu a để tính lượng nước còn lại trong bể (đơn vị (d{m^3})) khi (x = 7left( {dm} right)). Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Người ta đổ đầy nước vào một cái bể hình hộp chữ nhật, sau đó nhấn chìm một khối lập phương (đặc) có độ dài các cạnh bằng x(dm) vào trong bể. Biết rằng chiều rộng, chiều dài và chiều cao của bể lần lượt bằng \(x + 1,x + 3\) và \(x + 2\) (xem dưới đây).
a) Tìm đa thức biểu thị lượng nước còn lại trong bể. b) Xác định bậc, hệ số cao nhất và hệ số tự do của đa thức trong câu a. c) Sử dụng kết quả câu a để tính lượng nước còn lại trong bể (đơn vị \(d{m^3}\)) khi \(x = 7\left( {dm} \right)\). Phương pháp giải - Xem chi tiết a) Lượng nước còn lại trong bể= Thể tích khối lập phương- thể tích nước tràn ra. b) - Cho một đa thức. Khi đó: + Bậc của hạng tử có bậc cao nhất gọi là bậc của đa thức. + Hệ số của hạng tử có bậc cao nhất gọi là hệ số cao nhất. + Hệ số của hạng tử bậc 0 (hạng tử không chứa biến) gọi là hệ số tự do. c) Thay \(x = 7\left( {dm} \right)\) vào biểu thức biểu thị thể tích nước còn lại trong bể, tính được lượng nước còn lại trong bể. Lời giải chi tiết a) Thể tích bể nước là: \(V = \left( {x + 1} \right)\left( {x + 3} \right)\left( {x + 2} \right)\) \( = \left( {{x^2} + 4x + 3} \right)\left( {x + 2} \right)\) \( = {x^3} + 6{x^2} + 11x + 6\) Thể tích khối lập phương (ứng với lượng nước tràn) là: \({V_1} = {x^3}\). Lượng nước còn lại trong bể là: \({V_2}\left( x \right) = V - {V_1} = 6{x^2} + 11x + 6\left( {d{m^3}} \right)\). b) \({V_2}\left( x \right)\) là đa thức bậc hai, hệ số cao nhất bằng 6 và hệ số tự do bằng 6. c) Khi \(x = 7\), lượng nước còn lại trong bể là: \({V_2}\left( 7 \right) = {6.7^2} + 11.7 + 6 = 377\left( {d{m^3}} \right)\).
|