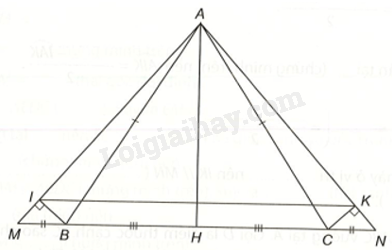
Giải bài 9 trang 108, 109, 110 vở thực hành Toán 7 tập 2Cho tam giác ABC cân tại đỉnh A. Gọi H là trung điểm của BC. a) Chứng minh (AH bot BC). b) Trên tia đối của tia BC lấy điểm M; trên tia đối của tia CB lấy điểm N sao cho (BM = CN). Chứng minh rằng (Delta ABM = Delta ACN). c) Gọi I là điểm trên AM, K là điểm trên AN sao cho (BI bot AM;CK bot AN). Chứng minh rằng tam giác AIK cân tại A, từ đó suy ra IK//MN. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho tam giác ABC cân tại đỉnh A. Gọi H là trung điểm của BC. a) Chứng minh AH⊥BC. b) Trên tia đối của tia BC lấy điểm M; trên tia đối của tia CB lấy điểm N sao cho BM=CN. Chứng minh rằng ΔABM=ΔACN. c) Gọi I là điểm trên AM, K là điểm trên AN sao cho BI⊥AM;CK⊥AN. Chứng minh rằng tam giác AIK cân tại A, từ đó suy ra IK//MN. Phương pháp giải - Xem chi tiết a) Tam giác ABC cân tại A nên AH là đường trung tuyến đồng thời là đường cao. b) + Vì ^ABM+^ABC=180o, ^ACN+^ACB=180o, ^ABC=^ACB nên ^ABM=^ACN. + Chứng minh ΔABM=ΔACN (c.g.c). c) + ΔBIM=ΔCKN (cạnh huyền – góc nhọn) nên MI=NK. Mà AM=AN nên AI=AK, suy ra ΔAIK cân tại A. Suy ra ^AIK=180o−^IAK2. + Chứng minh ΔAMN cân tại A nên ^AMN=180o−^MAN2. Suy ra ^AIK=^AMN suy ra IK//MN. Lời giải chi tiết
a) ΔABC cân tại A (giả thiết) Mà AH là đường trung tuyến (H là trung điểm của BC) Nên AH là đường cao của ΔABC (tính chất tam giác cân). Vậy AH⊥BC. b) Ta có: ^ABM+^ABC=180o (hai góc kề bù), ^ACN+^ACB=180o (hai góc kề bù). Mà ^ABC=^ACB nên ^ABM=^ACN ΔABM và ΔACN có: AB=AC (ΔABC cân tại đỉnh A). ^ABM=^ACN (chứng minh trên) BM=CN (giả thiết) Nên ΔABM=ΔACN (c.g.c). c) Ta có ΔABM=ΔACN (chứng minh trên) suy ra ^BMI=^CNK (hai góc tương ứng) và AM=AN (hai cạnh tương ứng). ΔBIM(^BIM=90o) và ΔCKN(^CKN=90o) có: BM=CN (giả thiết) ^BMI=^CNK (chứng minh trên) Nên ΔBIM=ΔCKN (cạnh huyền – góc nhọn). Suy ra MI=NK (hai cạnh tương ứng). Mà AM=AN (chứng minh trên) nên AI=AK, suy ra ΔAIK cân tại A (dấu hiệu nhận biết tam giác cân). Ta có AM=AN(chứng minh trên) nên ΔAMN cân tại A (dấu hiệu nhận biết tam giác cân). Suy ra ^AMN=180o−^MAN2. Ta có ΔAIK cân tại A (chứng minh trên) nên ^AIK=180o−^IAK2. Từ đó ^AIK=^AMN(=180o−^IAK2) Mà hai góc này ở vị trí đồng vị nên IK//MN (dấu hiệu nhận biết hai đường thẳng song song).  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
|
