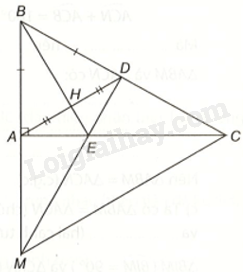
Giải bài 10 trang 110, 111 vở thực hành Toán 7 tập 2Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho (BD = BA) và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt BA tại M. Chứng minh rằng: a) (Delta ABH = Delta DBH). b) Tam giác AED cân. c) (EM > ED). d) Tam giác BCM là tam giác đều và (CE = 2EA), biết (widehat {ABC} = {60^o}). Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho \(BD = BA\) và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt BA tại M. Chứng minh rằng: a) \(\Delta ABH = \Delta DBH\). b) Tam giác AED cân. c) \(EM > ED\). d) Tam giác BCM là tam giác đều và \(CE = 2EA\), biết \(\widehat {ABC} = {60^o}\). Phương pháp giải - Xem chi tiết a) Chứng minh \(\Delta ABH = \Delta DBH\) (c.c.c). b) Chứng minh\(\Delta BAE = \Delta BDE\) (c.g.c) suy ra \(EA = ED\), suy ra tam giác AED cân. c) + Chứng minh \(\Delta EAM = \Delta EDC\) (g.c.g). Suy ra \(EM = EC\) + \(\Delta EDC\) vuông tại D nên \(EC > ED\). Do đó, \(EM > ED\). d) + Chỉ ra \(AM = DC\), mà \(BA = BD\) nên \(BM = BC\), suy ra \(\Delta BMC\) cân tại B. + Lại có \(\widehat {ABC} = {60^o}\) nên \(\Delta BMC\) là tam giác đều. + Chứng minh CA, MD là đường cao cũng là đường trung tuyến của \(\Delta BMC\), suy ra E là trọng tâm của \(\Delta BMC\) nên \(CE = 2EA\). Lời giải chi tiết
a) \(\Delta ABH\) và \(\Delta DBH\) có: \(BA = BD\) (theo giả thiết). BH là cạnh chung \(AH = DH\) (H là trung điểm của AD) Nên \(\Delta ABH = \Delta DBH\) (c.c.c). b) Ta có: \(\Delta ABH = \Delta DBH\) (chứng minh trên), suy ra \(\widehat {ABE} = \widehat {DBE}\) (hai góc tương ứng) \(\Delta BAE\) và \(\Delta BDE\) có: \(BA = BD\) (giả thiết). \(\widehat {ABE} = \widehat {DBE}\) (chứng minh trên) BE là cạnh chung Nên \(\Delta BAE = \Delta BDE\) (c.g.c) suy ra \(EA = ED\) (hai cạnh tương ứng). Nên \(\Delta ADE\) cân tại E (dấu hiệu nhận biết tam giác cân). c) \(\Delta BAE = \Delta BDE\) (chứng minh trên) nên \(\widehat {BDE} = \widehat {BAE} = {90^o}\). \(\Delta EAM\) và \(\Delta EDC\) có: \(\widehat {EAM} = \widehat {EDC} = {90^o}\), \(EA = ED\) (chứng minh trên), \(\widehat {AEM} = \widehat {DEC}\) (hai góc đối đỉnh). Nên \(\Delta EAM = \Delta EDC\) (g.c.g). Suy ra \(EM = EC\). \(\Delta EDC\) vuông tại D nên \(EC > ED\) (quan hệ giữa cạnh và góc trong tam giác). Mà \(EC = EM\) (chứng minh trên) nên \(EM > ED\). d) Ta có \(\Delta EAM = \Delta EDC\) (chứng minh trên) suy ra \(AM = DC\) (hai cạnh tương ứng). Mà \(BA = BD\) (giả thiết) nên \(BM = BC\). \(\Delta BMC\) có: \(BM = BC\) (chứng minh trên) Nên \(\Delta BMC\) cân tại B (dấu hiệu nhận biết tam giác cân). Mà \(\widehat {ABC} = {60^o}\). Nên \(\Delta BMC\) là tam giác đều. Mặt khác \(CA \bot BM\) nên CA là đường cao cũng là đường trung tuyến của \(\Delta BMC\), \(MD \bot BC\) nên MD là đường cao cũng là đường trung tuyến của \(\Delta BMC\). Từ đó suy ra E là trọng tâm của \(\Delta BMC\) nên \(CE = 2EA\).
|