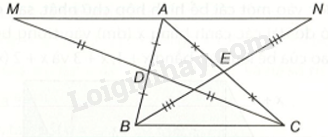
Giải bài 8 trang 107,108 vở thực hành Toán 7 tập 2Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho (DM = DC). a) Chứng minh rằng (Delta ADM = Delta BDC). Từ đó suy ra (AM = BC) và AM//BC. b) Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho (EN = EB). Chứng minh rằng AN//BC. c) Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho DM=DC. a) Chứng minh rằng ΔADM=ΔBDC. Từ đó suy ra AM=BC và AM//BC. b) Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho EN=EB. Chứng minh rằng AN//BC. c) Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN. Phương pháp giải - Xem chi tiết a) Chỉ ra AD=DB, ^ADM=^BDC, DM=DC suy ra ΔADM=ΔBDC (c.g.c), suy ra AM=BC và ^MAD=^CBD, suy ra AM//BC. b) Chứng minh ΔAEN=ΔCEB (c.g.c), suy ra ^EAN=^ECB, suy ra AN//BC. c) + Ta có AM//BC, AN//BC nên AM và AN trùng nhau, suy ra ba điểm M, A, N thẳng hàng. + Vì AM=BC và AN=BC, suy ra AM=AN nên A là trung điểm của MN. Lời giải chi tiết
a) ΔADM và ΔBDC có: AD=DB (do D là trung điểm của AB). ^ADM=^BDC (hai góc đối đỉnh) DM=DC (giả thiết) Nên ΔADM=ΔBDC (c.g.c). Suy ra AM=BC (hai cạnh tương ứng) và ^MAD=^CBD (hai góc tương ứng). Mà hai góc này ở vị trí so le trong nên AM//BC (dấu hiệu nhận biết hai đường thẳng song song). b) ΔAEN và ΔCEB có: AE=CE (do E là trung điểm của AC). ^AEN=^CEB (hai góc đối đỉnh) EN=EB (theo giả thiết) Nên ΔAEN=ΔCEB (c.g.c). Suy ra ^EAN=^ECB (hai góc tương ứng). Mà hai góc này ở vị trí so le trong nên AN//BC (dấu hiệu nhận biết hai đường thẳng song song). c) Ta có AM//BC (chứng minh trên), AN//BC (chứng minh trên) nên AM và AN trùng nhau (theo tiên đề Euclid). Từ đó suy ra ba điểm M, A, N thẳng hàng. Ta lại có AM=BC (chứng minh trên) và AN=BC (chứng minh trên), do đó AM=AN. Từ đó suy ra A là trung điểm của MN.  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 7 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả.
|
