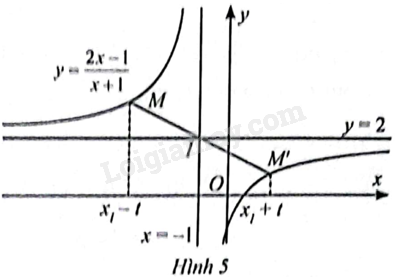
Giải bài 6 trang 32 sách bài tập toán 12 - Chân trời sáng tạo

Đề bài

Ta đã biết đồ thị hàm số $y = \frac{{2{\rm{x}} - 1}}{{x + 1}}$ có tiệm cận đứng là đường thẳng $x =  - 1$ và tiệm cận ngang là đường thẳng $y = 2$.

a) Tìm toạ độ giao điểm $I$ của đường tiệm cận.

b) Với $t$ tuỳ ý $\left( {t \ne 0} \right)$, gọi $M$ và $M'$ lần lượt là hai điểm trên đồ thị hàm số có hoành độ lần lượt là ${x_M} = {x_I} - t$ và ${x_{M'}} = {x_I} + t$. Tìm các tung độ $y\left( {{x_M}} \right)$ và $y\left( {{x_{M'}}} \right)$.

Từ đó, chứng minh rằng hai điểm $M$ và $M'$ đối xứng với nhau qua $I$.

Lời giải chi tiết

a) Đồ thị hàm số $y = \frac{{2{\rm{x}} - 1}}{{x + 1}}$ có tiệm cận đứng là đường thẳng $x =  - 1$ và tiệm cận ngang là đường thẳng $y = 2$ nên giao điểm của hai đường tiệm cận là $I\left( { - 1;2} \right)$.

b) Ta có: ${x_M} = {x_I} - t =  - 1 - t \Rightarrow {y_M} = \frac{{2{{\rm{x}}_M} - 1}}{{{x_M} + 1}} = \frac{{2\left( { - 1 - t} \right) - 1}}{{\left( { - 1 - t} \right) + 1}} = \frac{{2t + 3}}{t}$

${x_{M'}} = {x_I} + t =  - 1 + t \Rightarrow {y_{M'}} = \frac{{2{{\rm{x}}_{M'}} - 1}}{{{x_{M'}} + 1}} = \frac{{2\left( { - 1 + t} \right) - 1}}{{\left( { - 1 + t} \right) + 1}} = \frac{{2t - 3}}{t}$

Vì :

$\begin{array}{l}{x_M} + {x_{M'}} = \left( {{x_I} - t} \right) + \left( {{x_I} + t} \right) = 2{x_I};\\{y_M} + {y_{M'}} = \frac{{2t + 3}}{t} + \frac{{2t - 3}}{t} = \frac{{\left( {2t + 3} \right) + \left( {2t - 3} \right)}}{t} = 4 = 2{y_I}\end{array}$

nên $I$ là trung điểm của $MM'$.

Vậy hai điểm $M$ và $M'$ đối xứng với nhau qua $I$.