Đề thi, đề kiểm tra Toán lớp 11 - Chân trời sáng tạo

Đề thi giữa kì 2 Toán 11 Chân trời sáng tạo - Đề số 5

Tải về

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án
Làm đề thi

Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng. Với a là số thực khác 0 thì:

Đề bài

I. Trắc nghiệm
Câu 1 :

Chọn đáp án đúng.

Với a là số thực khác 0 thì:

  • A
    \({a^0} = 0\).
  • B
    \({a^0} = \frac{1}{a}\).
  • C
    \({a^0} =  - 1\).
  • D
    \({a^0} = 1\).
Câu 2 :

Cho biểu thức \(P = \sqrt[6]{x}\) với \(x > 0\). Mệnh đề nào dưới đây là đúng?

  • A
    \(P = {x^{\sqrt 6 }}\).
  • B
    \(P = {x^{\frac{1}{6}}}\).
  • C
    \(P = {x^6}\).
  • D
    \(P = {x^{ - 6}}\).
Câu 3 :

Chọn đáp án đúng:

  • A
    \(\sqrt[8]{{{{\left( {x - 1} \right)}^8}}} = x - 1\).
  • B
    \(\sqrt[8]{{{{\left( {x - 1} \right)}^8}}} = x + 1\).
  • C
    \(\sqrt[8]{{{{\left( {x - 1} \right)}^8}}} = \left| {x - 1} \right|\).
  • D
    \(\sqrt[8]{{{{\left( {x - 1} \right)}^8}}} =  - x + 1\).
Câu 4 :

Cho a là số dương, rút gọn biểu thức \(\frac{{\sqrt a .\sqrt[3]{{{a^2}}}}}{{\sqrt[4]{a}}}\) được kết quả là:

  • A
    \(\sqrt[{12}]{{{a^{11}}}}\).
  • B
    \(\sqrt[{121}]{a}\).
  • C
    \(\sqrt[{11}]{{{a^{12}}}}\).
  • D
    \(\sqrt[3]{{{a^4}}}\).
Câu 5 :

Giả sử một lọ nuôi cấy 100 con vi khuẩn lúc ban đầu và số lượng vi khuẩn tăng gấp đôi sau mỗi 2 giờ. Khi đó, số vi khuẩn N sau t giờ là \(N = {100.2^{\frac{t}{2}}}\) (con). Sau 4 giờ 30 phút thì có bao nhiêu con vi khuẩn? (làm tròn đến hàng đơn vị).

  • A
    474 con.
  • B
    475 con.
  • C
    476 con.
  • D
    477 con.
Câu 6 :

Cho hai số thực dương a, b với a khác 1. Số thực c để… được gọi là lôgarit cơ số a của b và kí hiệu là \({\log _a}b\).

Biểu thức phù hợp để điền vào “…” được câu đúng là:  

  • A
    \({a^c} = b\).
  • B
    \({a^b} = c\).
  • C
    \({b^a} = c\).
  • D
    \({c^a} = b\).
Câu 7 :

Chọn đáp án đúng.

Với \(a,b > 0,a \ne 1\) thì:

  • A
    \({\log _a}\left( {\frac{1}{b}} \right) =  - \frac{1}{{{{\log }_a}b}}\).
  • B
    \({\log _a}\left( {\frac{1}{b}} \right) =  - {\log _a}b\).
  • C
    \({\log _a}\left( {\frac{1}{b}} \right) = {\log _a}\left( { - b} \right)\).
  • D
    \({\log _a}\left( {\frac{1}{b}} \right) =  - {\log _a}\left( { - b} \right)\).
Câu 8 :

Chọn đáp án đúng:

Với n số thực dương \({b_1},{b_2},..,{b_n},a > 0,a \ne 1\) thì:

  • A
    \({\log _a}\left( {{b_1}.{b_2}...{b_n}} \right) = {\log _a}{b_1} + {\log _a}{b_2} + ... + {\log _a}{b_n}\).
  • B
    \({\log _a}\left( {{b_1}.{b_2}...{b_n}} \right) = {\log _a}{b_1}.{\log _a}{b_2}...{\log _a}{b_n}\).
  • C
    \({\log _a}\left( {{b_1} + {b_2} + ... + {b_n}} \right) = {\log _a}{b_1}.{\log _a}{b_2}...{\log _a}{b_n}\).
  • D
    \({\log _a}\left( {{b_1} + {b_2} + ... + {b_n}} \right) = {\log _a}{b_1} + {\log _a}{b_2} + ... + {\log _a}{b_n}\).
Câu 9 :

Cho x và y là các số dương. Khẳng định nào sau đây là đúng?

  • A
    \({3^{\ln x + \ln y}} = {3^{\ln x}} + {3^{\ln y}}\).
  • B
    \({3^{\ln \left( {x + y} \right)}} = {3^{\ln x}}{.3^{\ln y}}\).
  • C
    \({3^{\ln \left( {xy} \right)}} = {3^{\ln x}}{.3^{\ln y}}\).
  • D
    \({3^{\ln x.\ln y}} = {3^{\ln x}} + {3^{\ln y}}\).
Câu 10 :

Giá trị của biểu thức \(2{\log _5}10 + {\log _{25}}0,25\) là:

  • A
    \(\frac{1}{{{{\log }_{25}}50}}\).
  • B
    \(\frac{1}{{{{\log }_5}50}}\).
  • C
    \({\log _{25}}50\).
  • D
    \({\log _5}50\).
Câu 11 :

Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\) với giá trị nào của a dưới đây?

  • A
    \(a = \frac{1}{2}\).
  • B
    \(a = 0,75\).
  • C
    \(a = \frac{3}{2}\).
  • D
    \(a = \ln 2\).
Câu 12 :

Hàm số nào dưới đây là không phải hàm số mũ?

  • A
    \(y = {3^x}\).
  • B
    \(y = {\left( {3x} \right)^3}\).
  • C
    \(y = {\pi ^x}\).
  • D
    \(y = {\left( {\frac{1}{3}} \right)^x}\).
Câu 13 :

Hàm số nào sau đây có tập xác định là \(\mathbb{R}\)?

  • A
    \(y = \ln x\).
  • B
    \(y = \log \frac{x}{4}\).
  • C
    \(y = {e^{5x}}\).
  • D
    \(y = {\left( {\frac{2}{x}} \right)^5}\).
Câu 14 :

Hàm số \(y = {\log _{10}}x\) có tập giá trị là:

  • A
    \(\left( { - \infty ; + \infty } \right)\).
  • B
    \(\left( { - \infty ;0} \right)\).
  • C
    \(\left( {0; + \infty } \right)\).
  • D
    \(\left( { - 10;10} \right)\).
Câu 15 :

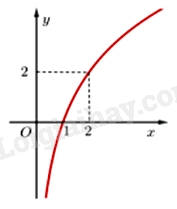
Cho đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) có đồ thị là hình dưới đây:

Tìm a.

  • A
    \(a = 2\).
  • B
    \(a = \sqrt 2 \).
  • C
    \(a = \frac{1}{{\sqrt 2 }}\).
  • D
    \(a = \frac{1}{2}\).
Câu 16 :

Có bao nhiêu giá trị nguyên của a để hàm số \(y = {\left( { - {a^2} + 2a + 4} \right)^x}\) đồng biến trên \(\mathbb{R}\)?

  • A
    1.
  • B
    2.
  • C
    3.
  • D
    4.
Câu 17 :

Cho bất phương trình \({6^x} > b\). Với giá trị nào của b thì bất phương trình đã cho có tập nghiệm là \(\mathbb{R}\)?

  • A
    \(b = 0\).
  • B
    \(b = 1\).
  • C
    \(b = \frac{1}{6}\).
  • D
    \(b = 6\).
Câu 18 :

Tập nghiệm của bất phương trình \({\left( {\frac{1}{{\sqrt {15} }}} \right)^x} > \frac{1}{{\sqrt {15} }}\) là

  • A
    \(S = \left[ {1; + \infty } \right)\).
  • B
    \(S = \left( { - \infty ;1} \right]\).
  • C
    \(S = \left( {1; + \infty } \right)\).
  • D
    \(S = \left( { - \infty ;1} \right)\).
Câu 19 :

Phương trình \({3^{ - x}} = 4\) có nghiệm là:  

  • A
    \(x = {\log _4}3\).
  • B
    \(x = {\log _3}4\).
  • C
    \(x =  - {\log _3}4\).
  • D
    \(x =  - {\log _4}3\).
Câu 20 :

Phương trình \({e^{2x}} - 5{e^x} = 0\) có bao nhiêu nghiệm?

  • A
    Vô nghiệm.
  • B
    1 nghiệm.
  • C
    2 nghiệm.
  • D
    3 nghiệm.
Câu 21 :

Tập nghiệm của phương trình: \({4^x} = \sqrt {2\sqrt 2 } \) là:  

  • A
    \(S = \left\{ {\frac{3}{8}} \right\}\).
  • B
    \(S = \left\{ {\frac{3}{4}} \right\}\).
  • C
    \(S = \left\{ {\frac{8}{3}} \right\}\).
  • D
    \(S = \left\{ {\frac{4}{3}} \right\}\).
Câu 22 :

Phương trình \({\log _{\sqrt[4]{2}}}{\left( {{x^2} - 2} \right)^2} = 8\) có bao nhiêu nghiệm?

  • A
    Vô nghiệm.
  • B
    1 nghiệm.
  • C
    2 nghiệm.
  • D
    3 nghiệm.
Câu 23 :

Bất phương trình \({3^{{4^x}}} < {4^{{3^x}}}\) có nghiệm là:

  • A
    \(x > {\log _{\frac{4}{3}}}\left( {{{\log }_4}3} \right)\).
  • B
    \(x < {\log _{\frac{4}{3}}}\left( {{{\log }_4}3} \right)\).
  • C
    \(x < {\log _{\frac{4}{3}}}\left( {{{\log }_3}4} \right)\).
  • D
    \(x > {\log _{\frac{4}{3}}}\left( {{{\log }_3}4} \right)\).
Câu 24 :

“Góc giữa hai đường thẳng a, b trong không gian, kí hiệu (a, b) là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt … hoặc … với a và b”. Từ (cụm từ) thích hợp để điền vào dấu … để được câu đúng là:

  • A
    vuông góc, trùng.
  • B
    vuông góc, chéo.
  • C
    song song, chéo.
  • D
    song song, trùng.
Câu 25 :

Cho hình chóp S. ABCD có AD//BC. Gọi N là một điểm thuộc cạnh SD (N khác S và D), qua N vẽ đường thẳng song song với AS cắt AD tại M. Chọn đáp án đúng:

  • A
    \(\left( {MN,BC} \right) = \left( {SA,SD} \right)\).
  • B
    \(\left( {MN,BC} \right) = \left( {SD,DA} \right)\).
  • C
    \(\left( {MN,BC} \right) = \left( {SA,AD} \right)\).
  • D
    Cả A, B, C đều sai.
Câu 26 :

Cho tứ diện ABCD có \(AB = CD = 2a\). Gọi M, N, I lần lượt là trung điểm của BC, AD, AC. Biết rằng \(MN = a\sqrt 3 \). Tính góc giữa hai đường thẳng AB và CD.

  • A
    \({90^0}\).
  • B
    \({60^0}\).
  • C
    \({30^0}\).
  • D
    \({70^0}\).
Câu 27 :

Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O, \(SA = SC\). Gọi I, K lần lượt là trung điểm của AB và BC. Góc giữa hai đường thẳng SO và IK bằng:

  • A
    \({60^0}\).
  • B
    \({90^0}\).
  • C
    \({120^0}\).
  • D
    \({70^0}\).
Câu 28 :

Cho hình chóp S.ABCD có \(SA \bot \left( {ABCD} \right)\). Tam giác SAC là tam giác gì?

  • A
    Tam giác vuông tại A.
  • B
    Tam giác cân tại A.
  • C
    Tam giác đều.
  • D
    Tam giác tù tại A.
Câu 29 :

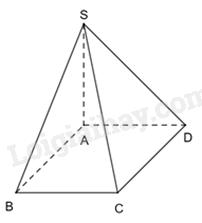
Cho hình chóp S. ABCD như hình vẽ dưới đây:

Biết rằng: \(SA \bot AB,SA \bot AD\).

Chọn khẳng định đúng.

  • A
    SA\( \bot \) (SAC).
  • B
    \(SA \bot \left( {ABCD} \right)\).
  • C
    Cả A và B đều đúng.
  • D
    Cả A và B đều sai.
Câu 30 :

Cho tứ diện OABC sao cho \(OA \bot \left( {OBC} \right)\). Gọi D là trung điểm của BC. Lấy điểm M bất kì thuộc cạnh AD (M khác A, D). Qua M kẻ đường thẳng song song với AO cắt OD tại N. Chọn đáp án đúng.

  • A
    \(MN \bot \left( {BOC} \right)\).
  • B
    \(MN \bot \left( {OAD} \right)\).
  • C
    Cả A và B đều đúng.
  • D
    Cả A và B đều sai.
Câu 31 :

Cho hình chóp S. ABCD. Gọi A là hình chiếu vuông góc của S lên mặt phẳng (ABCD). Khi đó, hình chiếu vuông góc của SC trên mặt phẳng (ABCD) là:

  • A
    AC.
  • B
    AD.
  • C
    AB.
  • D
    AS.
Câu 32 :

Cho hình chóp S.ABC. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC. Qua S kẻ đường thẳng vuông góc với mặt phẳng (ABC) và cắt mặt phẳng đó tại H. Khi đó, góc giữa SH và MP bằng bao nhiêu độ?

  • A
    \({60^0}\).
  • B
    \({90^0}\).
  • C
    \({120^0}\).
  • D
    \({70^0}\).
Câu 33 :

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Hình chiếu vuông góc của A trên mặt phẳng (COB) là điểm nào?

  • A
    Q (Q là trung điểm của OB).
  • B
    B.
  • C
    O.
  • D
    H (H là trung điểm của OC).
Câu 34 :

Cho tứ diện ABCD có tất cả các cạnh bằng nhau. Gọi M là trung điểm của CD. Góc giữa hai đường thẳng AB và CD bằng:

  • A
    \({30^0}\).
  • B
    \({60^0}\).
  • C
    \({90^0}\).
  • D
    \({45^0}\).
Câu 35 :

Cho hình chóp S. ABCD có đáy ABCD là hình vuông, \(SA \bot \left( {ABCD} \right)\).  Kẻ BM vuông góc với SC (M thuộc SC). Tam giác SMD là tam giác:

  • A
    Vuông tại M.
  • B
    Cân tại M.
  • C
    Tù tại M.
  • D
    Tam giác nhọn.
II. Tự luận
Câu 1 :

Cho hàm số: \(y = \frac{1}{4}\sqrt {\log \left( {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5} \right)} \).

a) Với \(m = 0\), hãy tìm tập xác định của hàm số trên.

b) Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định có tập xác định là \(\mathbb{R}\).
Câu 2 :

Cho hình vuông ABCD. Gọi H, K lần lượt là trung điểm của AB, AD. Trên đường thẳng vuông góc với (ABCD) tại H, lấy điểm S. Chứng minh rằng:

a) \(AC \bot \left( {SHK} \right)\).

b) \(CK \bot \left( {SDH} \right)\).
Câu 3 :

Giải bất phương trình \({\log _2}\left( {x - \sqrt {{x^2} - 1} } \right).{\log _3}\left( {x + \sqrt {{x^2} - 1} } \right) = {\log _6}\left| {x - \sqrt {{x^2} - 1} } \right|\).

Lời giải và đáp án

I. Trắc nghiệm
Câu 1 :

Chọn đáp án đúng.

Với a là số thực khác 0 thì:

  • A
    \({a^0} = 0\).
  • B
    \({a^0} = \frac{1}{a}\).
  • C
    \({a^0} =  - 1\).
  • D
    \({a^0} = 1\).

Đáp án : D

Phương pháp giải :

Với a là số thực khác 0 thì \({a^0} = 1\).

Lời giải chi tiết :

Với a là số thực khác 0 thì \({a^0} = 1\).

Đáp án D.

Câu 2 :

Cho biểu thức \(P = \sqrt[6]{x}\) với \(x > 0\). Mệnh đề nào dưới đây là đúng?

  • A
    \(P = {x^{\sqrt 6 }}\).
  • B
    \(P = {x^{\frac{1}{6}}}\).
  • C
    \(P = {x^6}\).
  • D
    \(P = {x^{ - 6}}\).

Đáp án : B

Phương pháp giải :

Cho số thực dương a và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m,n \in \mathbb{Z},n > 0\). Ta có: \({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\)

Lời giải chi tiết :

\(P = \sqrt[6]{x} = {x^{\frac{1}{6}}}\)

Đáp án B.

Câu 3 :

Chọn đáp án đúng:

  • A
    \(\sqrt[8]{{{{\left( {x - 1} \right)}^8}}} = x - 1\).
  • B
    \(\sqrt[8]{{{{\left( {x - 1} \right)}^8}}} = x + 1\).
  • C
    \(\sqrt[8]{{{{\left( {x - 1} \right)}^8}}} = \left| {x - 1} \right|\).
  • D
    \(\sqrt[8]{{{{\left( {x - 1} \right)}^8}}} =  - x + 1\).

Đáp án : C

Phương pháp giải :

\(\sqrt[n]{{{a^n}}} = \left| a \right|\) khi n chẵn (với các biểu thức đều có nghĩa).

Lời giải chi tiết :

\(\sqrt[8]{{{{\left( {x - 1} \right)}^8}}} = \left| {x - 1} \right|\).

Đáp án C.

Câu 4 :

Cho a là số dương, rút gọn biểu thức \(\frac{{\sqrt a .\sqrt[3]{{{a^2}}}}}{{\sqrt[4]{a}}}\) được kết quả là:

  • A
    \(\sqrt[{12}]{{{a^{11}}}}\).
  • B
    \(\sqrt[{121}]{a}\).
  • C
    \(\sqrt[{11}]{{{a^{12}}}}\).
  • D
    \(\sqrt[3]{{{a^4}}}\).

Đáp án : A

Phương pháp giải :

+ Cho số thực dương a và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m,n \in \mathbb{Z},n > 0\). Ta có: \({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\)

+ Với a là số thực dương, m, n là các số thực bất kì thì: \({a^m}.{a^n} = {a^{m + n}},{a^m}:{a^n} = {a^{m - n}}\).

Lời giải chi tiết :

\(\frac{{\sqrt a .\sqrt[3]{{{a^2}}}}}{{\sqrt[4]{a}}} = \frac{{{a^{\frac{1}{2}}}.{a^{\frac{2}{3}}}}}{{{a^{\frac{1}{4}}}}} = {a^{\frac{1}{2} + \frac{2}{3} - \frac{1}{4}}} = {a^{\frac{{11}}{{12}}}} = \sqrt[{12}]{{{a^{11}}}}\)

Đáp án A.

Câu 5 :

Giả sử một lọ nuôi cấy 100 con vi khuẩn lúc ban đầu và số lượng vi khuẩn tăng gấp đôi sau mỗi 2 giờ. Khi đó, số vi khuẩn N sau t giờ là \(N = {100.2^{\frac{t}{2}}}\) (con). Sau 4 giờ 30 phút thì có bao nhiêu con vi khuẩn? (làm tròn đến hàng đơn vị).

  • A
    474 con.
  • B
    475 con.
  • C
    476 con.
  • D
    477 con.

Đáp án : C

Phương pháp giải :

Thay t vào công thức $N={{100.2}^{\frac{t}{2}}}$ để tìm số con vi khuẩn.

Lời giải chi tiết :

Đổi 4 giờ 30 phút\( = \frac{9}{2}\) (giờ)

Sau \(\frac{9}{2}\) giờ sẽ có số con vi khuẩn là: \({100.2^{\frac{{\frac{9}{2}}}{2}}} = {100.2^{\frac{9}{4}}} \approx 476\) (con).

Đáp án C.

Câu 6 :

Cho hai số thực dương a, b với a khác 1. Số thực c để… được gọi là lôgarit cơ số a của b và kí hiệu là \({\log _a}b\).

Biểu thức phù hợp để điền vào “…” được câu đúng là:  

  • A
    \({a^c} = b\).
  • B
    \({a^b} = c\).
  • C
    \({b^a} = c\).
  • D
    \({c^a} = b\).

Đáp án : A

Phương pháp giải :

Cho hai số thực dương a, b với a khác 1. Số thực c để \({a^c} = b\) được gọi là lôgarit cơ số a của b và kí hiệu \({\log _a}b\).

Lời giải chi tiết :

Cho hai số thực dương a, b với a khác 1. Số thực c để \({a^c} = b\) được gọi là lôgarit cơ số a của b và kí hiệu \({\log _a}b\).

Đáp án A.

Câu 7 :

Chọn đáp án đúng.

Với \(a,b > 0,a \ne 1\) thì:

  • A
    \({\log _a}\left( {\frac{1}{b}} \right) =  - \frac{1}{{{{\log }_a}b}}\).
  • B
    \({\log _a}\left( {\frac{1}{b}} \right) =  - {\log _a}b\).
  • C
    \({\log _a}\left( {\frac{1}{b}} \right) = {\log _a}\left( { - b} \right)\).
  • D
    \({\log _a}\left( {\frac{1}{b}} \right) =  - {\log _a}\left( { - b} \right)\).

Đáp án : B

Phương pháp giải :

Với \(a,b > 0,a \ne 1\) thì \({\log _a}\left( {\frac{1}{b}} \right) =  - {\log _a}b\)

Lời giải chi tiết :

\({\log _a}\left( {\frac{1}{b}} \right) =  - {\log _a}b\)

Đáp án B.

Câu 8 :

Chọn đáp án đúng:

Với n số thực dương \({b_1},{b_2},..,{b_n},a > 0,a \ne 1\) thì:

  • A
    \({\log _a}\left( {{b_1}.{b_2}...{b_n}} \right) = {\log _a}{b_1} + {\log _a}{b_2} + ... + {\log _a}{b_n}\).
  • B
    \({\log _a}\left( {{b_1}.{b_2}...{b_n}} \right) = {\log _a}{b_1}.{\log _a}{b_2}...{\log _a}{b_n}\).
  • C
    \({\log _a}\left( {{b_1} + {b_2} + ... + {b_n}} \right) = {\log _a}{b_1}.{\log _a}{b_2}...{\log _a}{b_n}\).
  • D
    \({\log _a}\left( {{b_1} + {b_2} + ... + {b_n}} \right) = {\log _a}{b_1} + {\log _a}{b_2} + ... + {\log _a}{b_n}\).

Đáp án : A

Phương pháp giải :

Với n số thực dương \({b_1},{b_2},..,{b_n}\) thì: \({\log _a}\left( {{b_1}.{b_2}...{b_n}} \right) = {\log _a}{b_1} + {\log _a}{b_2} + ... + {\log _a}{b_n}\)

Lời giải chi tiết :

Với n số thực dương \({b_1},{b_2},..,{b_n}\) thì: \({\log _a}\left( {{b_1}.{b_2}...{b_n}} \right) = {\log _a}{b_1} + {\log _a}{b_2} + ... + {\log _a}{b_n}\)

Đáp án A.

Câu 9 :

Cho x và y là các số dương. Khẳng định nào sau đây là đúng?

  • A
    \({3^{\ln x + \ln y}} = {3^{\ln x}} + {3^{\ln y}}\).
  • B
    \({3^{\ln \left( {x + y} \right)}} = {3^{\ln x}}{.3^{\ln y}}\).
  • C
    \({3^{\ln \left( {xy} \right)}} = {3^{\ln x}}{.3^{\ln y}}\).
  • D
    \({3^{\ln x.\ln y}} = {3^{\ln x}} + {3^{\ln y}}\).

Đáp án : C

Phương pháp giải :

+ Với a là số thực dương, m, n là các số thực bất kì thì: \({a^m}.{a^n} = {a^{m + n}}\).

+ Với \(a > 0,a \ne 1,b,c > 0\) thì \(\ln x + \ln y = \ln \left( {xy} \right)\).

Lời giải chi tiết :

Ta có: \({3^{\ln x}}{.3^{\ln y}} = {3^{\ln x + \ln y}} = {3^{\ln \left( {xy} \right)}}\)

Đáp án C.

Câu 10 :

Giá trị của biểu thức \(2{\log _5}10 + {\log _{25}}0,25\) là:

  • A
    \(\frac{1}{{{{\log }_{25}}50}}\).
  • B
    \(\frac{1}{{{{\log }_5}50}}\).
  • C
    \({\log _{25}}50\).
  • D
    \({\log _5}50\).

Đáp án : D

Phương pháp giải :

Với \(a > 0,a \ne 1,b,c > 0\) thì: \({\log _a}b + {\log _a}c = {\log _a}\left( {bc} \right)\), \({\log _{{b^a}}}c = \frac{1}{a}{\log _b}c\), \(\alpha {\log _a}b = {\log _a}{b^\alpha }\) \(\left( {\alpha  \in \mathbb{R}} \right)\)

Lời giải chi tiết :

\(2{\log _5}10 + {\log _{25}}0,25 = {\log _5}{10^2} + \frac{1}{2}{\log _5}0,25 = {\log _5}100 + {\log _5}0,{25^{\frac{1}{2}}} = {\log _5}\left( {100.0,5} \right) = {\log _5}50\)

Đáp án D.

Câu 11 :

Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\) với giá trị nào của a dưới đây?

  • A
    \(a = \frac{1}{2}\).
  • B
    \(a = 0,75\).
  • C
    \(a = \frac{3}{2}\).
  • D
    \(a = \ln 2\).

Đáp án : C

Phương pháp giải :

Hàm số \(y = {\log _a}x\) đồng biến trên \(\left( {0; + \infty } \right)\) với \(a > 1\).

Lời giải chi tiết :

Vì hàm số \(y = {\log _a}x\) đồng biến trên \(\left( {0; + \infty } \right)\) với \(a > 1\) nên hàm số đồng biến khi \(a = \frac{3}{2}\).

Đáp án C.

Câu 12 :

Hàm số nào dưới đây là không phải hàm số mũ?

  • A
    \(y = {3^x}\).
  • B
    \(y = {\left( {3x} \right)^3}\).
  • C
    \(y = {\pi ^x}\).
  • D
    \(y = {\left( {\frac{1}{3}} \right)^x}\).

Đáp án : B

Phương pháp giải :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a.

Lời giải chi tiết :

Hàm số \(y = {\left( {3x} \right)^3}\) không phải là hàm số mũ.

Đáp án B.

Câu 13 :

Hàm số nào sau đây có tập xác định là \(\mathbb{R}\)?

  • A
    \(y = \ln x\).
  • B
    \(y = \log \frac{x}{4}\).
  • C
    \(y = {e^{5x}}\).
  • D
    \(y = {\left( {\frac{2}{x}} \right)^5}\).

Đáp án : C

Phương pháp giải :

Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là \(\mathbb{R}\).

Hàm số \(y = {\log _a}u\left( x \right)\left( {a > 0,a \ne 1} \right)\) xác định khi \(u\left( x \right) > 0\).

Lời giải chi tiết :

Hàm số \(y = {e^{5x}}\) có tập xác định là \(\mathbb{R}\).

Đáp án C.

Câu 14 :

Hàm số \(y = {\log _{10}}x\) có tập giá trị là:

  • A
    \(\left( { - \infty ; + \infty } \right)\).
  • B
    \(\left( { - \infty ;0} \right)\).
  • C
    \(\left( {0; + \infty } \right)\).
  • D
    \(\left( { - 10;10} \right)\).

Đáp án : A

Phương pháp giải :

Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) có tập giá trị là \(\left( { - \infty ; + \infty } \right)\).

Lời giải chi tiết :

Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) có tập giá trị là \(\left( { - \infty ; + \infty } \right)\).

Đáp án A.

Câu 15 :

Cho đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) có đồ thị là hình dưới đây:

Tìm a.

  • A
    \(a = 2\).
  • B
    \(a = \sqrt 2 \).
  • C
    \(a = \frac{1}{{\sqrt 2 }}\).
  • D
    \(a = \frac{1}{2}\).

Đáp án : B

Phương pháp giải :

Thay điểm A(2; 2) vào hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) để tìm a.

Lời giải chi tiết :

Vì đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) đi qua điểm A(2; 2) nên ta có:

\({\log _a}2 = 2 \Leftrightarrow {a^2} = 2 \Rightarrow a = \sqrt 2 \) (do \(a > 0,a \ne 1\))

Đáp án B.

Câu 16 :

Có bao nhiêu giá trị nguyên của a để hàm số \(y = {\left( { - {a^2} + 2a + 4} \right)^x}\) đồng biến trên \(\mathbb{R}\)?

  • A
    1.
  • B
    2.
  • C
    3.
  • D
    4.

Đáp án : C

Phương pháp giải :

Cho hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\):

+ Nếu \(a > 1\) thì hàm số đồng biến trên \(\mathbb{R}\).

+ Nếu \(0 < a < 1\) thì hàm số nghịch biến trên \(\mathbb{R}\).

Lời giải chi tiết :

Hàm số \(y = {\left( { - {a^2} + 2a + 4} \right)^x}\) đồng biến trên \(\mathbb{R}\) khi:

\( - {a^2} + 2a + 4 > 1 \Leftrightarrow  - {a^2} + 2a + 3 > 0 \Leftrightarrow {a^2} - 2a - 3 < 0 \Leftrightarrow \left( {a + 1} \right)\left( {a - 3} \right) < 0 \Leftrightarrow  - 1 < a < 3\)

Mà a là số nguyên nên \(a \in \left\{ {0;1;2} \right\}\).

Vậy có 3 giá trị nguyên của a để hàm số \(y = {\left( { - {a^2} + 2a + 4} \right)^x}\) đồng biến trên \(\mathbb{R}\).

Đáp án C.

Câu 17 :

Cho bất phương trình \({6^x} > b\). Với giá trị nào của b thì bất phương trình đã cho có tập nghiệm là \(\mathbb{R}\)?

  • A
    \(b = 0\).
  • B
    \(b = 1\).
  • C
    \(b = \frac{1}{6}\).
  • D
    \(b = 6\).

Đáp án : A

Phương pháp giải :

Bất phương trình \({a^x} > b\left( {0 < a \ne 1} \right)\) có tập nghiệm là \(\mathbb{R}\) khi \(b \le 0\).

Lời giải chi tiết :

Bất phương trình \({a^x} > b\left( {0 < a \ne 1} \right)\) có tập nghiệm là \(\mathbb{R}\) khi \(b \le 0\) nên bất phương trình \({6^x} > b\) có có tập nghiệm là \(\mathbb{R}\) với \(b = 0\)

Đáp án A.

Câu 18 :

Tập nghiệm của bất phương trình \({\left( {\frac{1}{{\sqrt {15} }}} \right)^x} > \frac{1}{{\sqrt {15} }}\) là

  • A
    \(S = \left[ {1; + \infty } \right)\).
  • B
    \(S = \left( { - \infty ;1} \right]\).
  • C
    \(S = \left( {1; + \infty } \right)\).
  • D
    \(S = \left( { - \infty ;1} \right)\).

Đáp án : D

Phương pháp giải :

Với \(0 < a < 1\) thì \({a^{u\left( x \right)}} > {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) < v\left( x \right)\).

Lời giải chi tiết :

\({\left( {\frac{1}{{\sqrt {15} }}} \right)^x} > \frac{1}{{\sqrt {15} }} \Leftrightarrow x < 1\) (do \(0 < \frac{1}{{\sqrt {15} }} < 1\))

Vậy tập nghiệm của bất phương trình là: \(S = \left( { - \infty ;1} \right)\)

Đáp án D.

Câu 19 :

Phương trình \({3^{ - x}} = 4\) có nghiệm là:  

  • A
    \(x = {\log _4}3\).
  • B
    \(x = {\log _3}4\).
  • C
    \(x =  - {\log _3}4\).
  • D
    \(x =  - {\log _4}3\).

Đáp án : C

Phương pháp giải :

Phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\) với \(b > 0\) có nghiệm là: \(x = {\log _a}b\)

Lời giải chi tiết :

\({3^{ - x}} = 4 \Leftrightarrow  - x = {\log _3}4 \Leftrightarrow x =  - {\log _3}4\)

Vậy phương trình có nghiệm \(x =  - {\log _3}4\).

Đáp án C.

Câu 20 :

Phương trình \({e^{2x}} - 5{e^x} = 0\) có bao nhiêu nghiệm?

  • A
    Vô nghiệm.
  • B
    1 nghiệm.
  • C
    2 nghiệm.
  • D
    3 nghiệm.

Đáp án : B

Phương pháp giải :

Phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\) với \(b > 0\) có nghiệm là: \(x = {\log _a}b\)

Lời giải chi tiết :

\({e^{2x}} - 5{e^x} = 0 \Leftrightarrow {\left( {{e^x}} \right)^2} - 5{e^x} = 0 \Leftrightarrow {e^x}\left( {{e^x} - 5} \right) = 0 \Leftrightarrow {e^x} - 5 = 0\left( {do\;{e^x} > 0\;\forall x \in \mathbb{R}} \right) \Leftrightarrow x = \ln 5\)

Vậy phương trình đã cho có một nghiệm.

Đáp án B.

Câu 21 :

Tập nghiệm của phương trình: \({4^x} = \sqrt {2\sqrt 2 } \) là:  

  • A
    \(S = \left\{ {\frac{3}{8}} \right\}\).
  • B
    \(S = \left\{ {\frac{3}{4}} \right\}\).
  • C
    \(S = \left\{ {\frac{8}{3}} \right\}\).
  • D
    \(S = \left\{ {\frac{4}{3}} \right\}\).

Đáp án : A

Phương pháp giải :

Với \(a > 0,a \ne 1\) ta có: \({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)\)

Lời giải chi tiết :

\({4^x} = \sqrt {2\sqrt 2 }  \Leftrightarrow {2^{2x}} = {\left( {{{2.2}^{\frac{1}{2}}}} \right)^{\frac{1}{2}}} \Leftrightarrow {2^{2x}} = {2^{\frac{3}{4}}} \Leftrightarrow 2x = \frac{3}{4} \Leftrightarrow x = \frac{3}{8}\)

Vậy tập nghiệm của phương trình là: \(S = \left\{ {\frac{3}{8}} \right\}\)

Đáp án A.

Câu 22 :

Phương trình \({\log _{\sqrt[4]{2}}}{\left( {{x^2} - 2} \right)^2} = 8\) có bao nhiêu nghiệm?

  • A
    Vô nghiệm.
  • B
    1 nghiệm.
  • C
    2 nghiệm.
  • D
    3 nghiệm.

Đáp án : D

Phương pháp giải :

Với \(a > 0,a \ne 1\) ta có: \({\log _a}u\left( x \right) = b \Leftrightarrow u\left( x \right) = {a^b}\)

Lời giải chi tiết :

\({\log _{\sqrt[4]{2}}}{\left( {{x^2} - 2} \right)^2} = 8 \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 2 \ne 0\\{\left( {{x^2} - 2} \right)^2} = {\left( {\sqrt[4]{2}} \right)^8}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 2 \ne 0\\{\left( {{x^2} - 2} \right)^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne  \pm \sqrt 2 \\\left[ \begin{array}{l}{x^2} - 2 = 2\\{x^2} - 2 =  - 2\end{array} \right.\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x \ne  \pm \sqrt 2 \\\left[ \begin{array}{l}{x^2} = 4\\{x^2} = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne  \pm \sqrt 2 \\\left[ \begin{array}{l}x =  \pm 2\\x = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  \pm 2\\x = 0\end{array} \right.\)

Vậy phương trình đã cho có 3 nghiệm.

Đáp án D.

Câu 23 :

Bất phương trình \({3^{{4^x}}} < {4^{{3^x}}}\) có nghiệm là:

  • A
    \(x > {\log _{\frac{4}{3}}}\left( {{{\log }_4}3} \right)\).
  • B
    \(x < {\log _{\frac{4}{3}}}\left( {{{\log }_4}3} \right)\).
  • C
    \(x < {\log _{\frac{4}{3}}}\left( {{{\log }_3}4} \right)\).
  • D
    \(x > {\log _{\frac{4}{3}}}\left( {{{\log }_3}4} \right)\).

Đáp án : C

Phương pháp giải :

Với \(a > 1,b > 0\) thì \({a^{u\left( x \right)}} < b \Leftrightarrow u\left( x \right) < {\log _a}b\).

Lời giải chi tiết :

\({3^{{4^x}}} < {4^{{3^x}}} \Leftrightarrow {4^x}{\log _3}3 < {3^x}{\log _3}4 \Leftrightarrow {\left( {\frac{4}{3}} \right)^x} < {\log _3}4 \Leftrightarrow x < {\log _{\frac{4}{3}}}\left( {{{\log }_3}4} \right)\)

Vậy bất phương trình đã cho có nghiệm là \(x < {\log _{\frac{4}{3}}}\left( {{{\log }_3}4} \right)\)

Đáp án C.

Câu 24 :

“Góc giữa hai đường thẳng a, b trong không gian, kí hiệu (a, b) là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt … hoặc … với a và b”. Từ (cụm từ) thích hợp để điền vào dấu … để được câu đúng là:

  • A
    vuông góc, trùng.
  • B
    vuông góc, chéo.
  • C
    song song, chéo.
  • D
    song song, trùng.

Đáp án : D

Phương pháp giải :

Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\).

Lời giải chi tiết :

Góc giữa hai đường thẳng a, b trong không gian, kí hiệu (a, b) là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song hoặc trùng với a và b

Đáp án D.

Câu 25 :

Cho hình chóp S. ABCD có AD//BC. Gọi N là một điểm thuộc cạnh SD (N khác S và D), qua N vẽ đường thẳng song song với AS cắt AD tại M. Chọn đáp án đúng:

  • A
    \(\left( {MN,BC} \right) = \left( {SA,SD} \right)\).
  • B
    \(\left( {MN,BC} \right) = \left( {SD,DA} \right)\).
  • C
    \(\left( {MN,BC} \right) = \left( {SA,AD} \right)\).
  • D
    Cả A, B, C đều sai.

Đáp án : C

Phương pháp giải :

Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\)

Lời giải chi tiết :

Vì AD//BC, MN//SA nên \(\left( {MN,BC} \right) = \left( {SA,AD} \right)\)

Đáp án C.

Câu 26 :

Cho tứ diện ABCD có \(AB = CD = 2a\). Gọi M, N, I lần lượt là trung điểm của BC, AD, AC. Biết rằng \(MN = a\sqrt 3 \). Tính góc giữa hai đường thẳng AB và CD.

  • A
    \({90^0}\).
  • B
    \({60^0}\).
  • C
    \({30^0}\).
  • D
    \({70^0}\).

Đáp án : B

Phương pháp giải :

+ Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\).

+ Góc giữa hai đường thẳng không vượt quá \({90^0}\).

Lời giải chi tiết :

Vì IM là đường trung bình của tam giác ABC nên IM//AB và \(IM = \frac{{AB}}{2} = a\)

Vì IN là đường trung bình của tam giác ADC nên IN//CD và \(IN = \frac{{CD}}{2} = a\)

Do đó, \(\left( {AB,CD} \right) = \left( {IM,IN} \right)\)

Áp dụng định lí côsin vào tam giác MNI ta có:

\(M{N^2} = I{M^2} + I{N^2} - 2IM.IN.\cos \widehat {MIN} \Rightarrow 3{a^2} = {a^2} + {a^2} - 2a.a.\cos \widehat {MIN} \Rightarrow \cos \widehat {MIN} = \frac{{ - 1}}{2} \Rightarrow \widehat {MIN} = {120^0}\)

Suy ra: \(\left( {AB,CD} \right) = \left( {IM,IN} \right) = {180^0} - \widehat {MIN} = {180^0} - {120^0} = {60^0}\)

Đáp án B.

Câu 27 :

Cho hình chóp S. ABCD có đáy ABCD là hình thoi tâm O, \(SA = SC\). Gọi I, K lần lượt là trung điểm của AB và BC. Góc giữa hai đường thẳng SO và IK bằng:

  • A
    \({60^0}\).
  • B
    \({90^0}\).
  • C
    \({120^0}\).
  • D
    \({70^0}\).

Đáp án : B

Phương pháp giải :

+ Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

+ Hai đường thẳng a, b được gọi là vuông góc với nhau nếu góc giữa chúng bằng \({90^0}\).

Lời giải chi tiết :

Vì tứ giác ABCD là hình thoi nên O là trung điểm của AC.

Vì \(SA = SC\) nên tam giác SAC cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao. Do đó, \(SO \bot AC\)

Vì I, K lần lượt là trung điểm của AB và BC nên IK là đường trung bình của tam giác BAC. Do đó, IK//AC.

Vì \(SO \bot AC\), IK//AC nên \(IK \bot SO\). Do đó, góc giữa hai đường thẳng SO và IK bằng \({90^0}\).

Đáp án B.

Câu 28 :

Cho hình chóp S.ABCD có \(SA \bot \left( {ABCD} \right)\). Tam giác SAC là tam giác gì?

  • A
    Tam giác vuông tại A.
  • B
    Tam giác cân tại A.
  • C
    Tam giác đều.
  • D
    Tam giác tù tại A.

Đáp án : A

Phương pháp giải :

Đường thẳng d gọi là vuông góc với mặt phẳng (P) nếu nó vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P).

Lời giải chi tiết :

Vì \(SA \bot \left( {ABCD} \right),AC \subset \left( {ABCD} \right) \Rightarrow SA \bot AC\). Do đó, tam giác SAC vuông tại A.

Đáp án A.

Câu 29 :

Cho hình chóp S. ABCD như hình vẽ dưới đây:

Biết rằng: \(SA \bot AB,SA \bot AD\).

Chọn khẳng định đúng.

  • A
    SA\( \bot \) (SAC).
  • B
    \(SA \bot \left( {ABCD} \right)\).
  • C
    Cả A và B đều đúng.
  • D
    Cả A và B đều sai.

Đáp án : B

Phương pháp giải :

Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\)

Lời giải chi tiết :

Vì \(SA \bot AB,SA \bot AD\), AB và AD cắt nhau tại A và nằm trong mặt phẳng (ABCD) nên \(SA \bot \left( {ABCD} \right)\).

SA không vuông góc với mặt phẳng (SAC).

Đáp án B.

Câu 30 :

Cho tứ diện OABC sao cho \(OA \bot \left( {OBC} \right)\). Gọi D là trung điểm của BC. Lấy điểm M bất kì thuộc cạnh AD (M khác A, D). Qua M kẻ đường thẳng song song với AO cắt OD tại N. Chọn đáp án đúng.

  • A
    \(MN \bot \left( {BOC} \right)\).
  • B
    \(MN \bot \left( {OAD} \right)\).
  • C
    Cả A và B đều đúng.
  • D
    Cả A và B đều sai.

Đáp án : A

Phương pháp giải :

Nếu đường thẳng a vuông góc với mặt phẳng (P) thì các đường thẳng song song với a cũng vuông góc với (P).

Lời giải chi tiết :

Vì \(OA \bot \left( {OBC} \right),\)MN//OA nên \(MN \bot \left( {OBC} \right)\)

MN không vuông góc với mặt phẳng (OAD).

Đáp án A.

Câu 31 :

Cho hình chóp S. ABCD. Gọi A là hình chiếu vuông góc của S lên mặt phẳng (ABCD). Khi đó, hình chiếu vuông góc của SC trên mặt phẳng (ABCD) là:

  • A
    AC.
  • B
    AD.
  • C
    AB.
  • D
    AS.

Đáp án : A

Phương pháp giải :

Cho mặt phẳng (P). Xét một điểm M tùy ý trong không gian. Gọi d là đường thẳng đi qua điểm M và vuông góc với (P). Gọi M’ là giao điểm của đường thẳng d và mặt phẳng (P). Khi đó, điểm M’ được gọi là hình chiếu vuông góc của điểm M lên mặt phẳng (P).

Lời giải chi tiết :

Vì C thuộc mặt phẳng (ABCD) nên hình chiếu vuông góc của điểm C trên mặt phẳng (ABCD) là chính nó.

Vì A là hình chiếu của S trên mặt phẳng (ABCD).

Do đó, hình chiếu vuông góc của SC trên mặt phẳng (ABCD) là AC.

Đáp án A.

Câu 32 :

Cho hình chóp S.ABC. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC. Qua S kẻ đường thẳng vuông góc với mặt phẳng (ABC) và cắt mặt phẳng đó tại H. Khi đó, góc giữa SH và MP bằng bao nhiêu độ?

  • A
    \({60^0}\).
  • B
    \({90^0}\).
  • C
    \({120^0}\).
  • D
    \({70^0}\).

Đáp án : B

Phương pháp giải :

+ Nếu đường thẳng d vuông góc với mặt phẳng (P) thì đường thẳng d cũng vuông góc với các mặt phẳng song song với (P).

+ Đường thẳng d gọi là vuông góc với mặt phẳng (P) nếu nó vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P).

Lời giải chi tiết :

Vì M, N lần lượt là trung điểm của SA, SB nên MN là đường trung bình của tam giác SAB. Do đó, MN//AB.

Vì P, N lần lượt là trung điểm của SC, SB nên PN là đường trung bình của tam giác SBC. Do đó, PN//CB.

Vì MN//AB, PN//CB nên (MNP)// (ABC).

Mặt khác, \(SH \bot \left( {ABC} \right)\) nên \(SH \bot \left( {MNP} \right)\). Mà \(MP \subset \left( {MNP} \right) \Rightarrow SH \bot MP\)

Do đó, góc giữa hai đường thẳng MP và SH bằng \({90^0}\).

Đáp án B.

Câu 33 :

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Hình chiếu vuông góc của A trên mặt phẳng (COB) là điểm nào?

  • A
    Q (Q là trung điểm của OB).
  • B
    B.
  • C
    O.
  • D
    H (H là trung điểm của OC).

Đáp án : C

Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Cho mặt phẳng (P). Xét một điểm M tùy ý trong không gian. Gọi d là đường thẳng đi qua điểm M và vuông góc với (P). Gọi M’ là giao điểm của đường thẳng d và mặt phẳng (P). Khi đó, điểm M’ được gọi là hình chiếu vuông góc của điểm M lên mặt phẳng (P).

Lời giải chi tiết :

Vì \(OA \bot OB,OA \bot OC\) và OB và OC cắt nhau tại O và nằm trong mặt phẳng (OBC) nên \(OA \bot \left( {OBC} \right)\) nên O là hình chiếu vuông góc của A trên mặt phẳng (COB).

Đáp án C.

Câu 34 :

Cho tứ diện ABCD có tất cả các cạnh bằng nhau. Gọi M là trung điểm của CD. Góc giữa hai đường thẳng AB và CD bằng:

  • A
    \({30^0}\).
  • B
    \({60^0}\).
  • C
    \({90^0}\).
  • D
    \({45^0}\).

Đáp án : C

Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì \(AC = AD = CD\) nên tam giác ACD là tam giác đều. Do đó, AM là đường trung tuyến đồng thời là đường cao. Do đó, \(AM \bot CD\)

Vì \(BC = BD = CD\) nên tam giác BCD là tam giác đều. Do đó, BM là đường trung tuyến đồng thời là đường cao. Do đó, \(BM \bot CD\)

Vì \(AM \bot CD\), \(BM \bot CD\), AM, BM cắt nhau tại M và nằm trong mặt phẳng ABM.

Do đó, \(CD \bot \left( {AMB} \right)\). Mà \(AB \subset \left( {ABM} \right) \Rightarrow AB \bot CD\)

Do đó, góc giữa hai đường thẳng AB và CD bằng \({90^0}\).

Đáp án C.

Câu 35 :

Cho hình chóp S. ABCD có đáy ABCD là hình vuông, \(SA \bot \left( {ABCD} \right)\).  Kẻ BM vuông góc với SC (M thuộc SC). Tam giác SMD là tam giác:

  • A
    Vuông tại M.
  • B
    Cân tại M.
  • C
    Tù tại M.
  • D
    Tam giác nhọn.

Đáp án : A

Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

Vì ABCD là hình vuông nên \(AC \bot BD\)

Vì \(SA \bot \left( {ABCD} \right),BD \subset \left( {ABCD} \right) \Rightarrow SA \bot BD\)

Ta có: \(AC \bot BD\), \(SA \bot BD\), SA, AC cắt nhau tại A và nằm trong mặt phẳng (SAC) nên \(BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\)

Lại có: \(BM \bot SC\), BM và BD cắt nhau tại B và nằm trong mặt phẳng (BMD) nên \(SC \bot \left( {BMD} \right)\).

Mà \(MD \subset \left( {BMD} \right) \Rightarrow MD \bot SC\) hay \(MD \bot SM\). Do đó, tam giác SMD vuông tại M.

Đáp án A.

II. Tự luận
Câu 1 :

Cho hàm số: \(y = \frac{1}{4}\sqrt {\log \left( {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5} \right)} \).

a) Với \(m = 0\), hãy tìm tập xác định của hàm số trên.

b) Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định có tập xác định là \(\mathbb{R}\).
Phương pháp giải :

Hàm số \(y = \log u\left( x \right)\) xác định khi \(u\left( x \right) > 0\).

Hàm số \(y = \sqrt {u\left( x \right)} \) xác định khi \(u\left( x \right) \ge 0\).

Lời giải chi tiết :

a) Với \(m = 0\) ta có: \(y = \frac{1}{4}\sqrt {\log \left( {{x^2} - 2x + 5} \right)} \).

Hàm số \(y = \frac{1}{4}\sqrt {\log \left( {{x^2} - 2x + 5} \right)} \) xác định khi

\(\log \left( {{x^2} - 2x + 5} \right) > 0 \Leftrightarrow {x^2} - 2x + 5 > 1 \Leftrightarrow {x^2} - 2x + 4 > 0 \Leftrightarrow {\left( {x - 1} \right)^2} + 3 > 0\) (luôn đúng với mọi số thực x)

Vậy với \(m = 0\) thì tập xác định của hàm số là: \(D = \left( { - \infty ; + \infty } \right)\)

b) Hàm số \(y = \frac{1}{4}\sqrt {\log \left( {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5} \right)} \)

Điều kiện: \(\log \left( {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5} \right) \ge 0\) với mọi \(x \in \mathbb{R}\)

\( \Leftrightarrow \left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5 \ge 1\) với mọi \(x \in \mathbb{R}\)

\( \Leftrightarrow \left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 4 \ge 0\) với mọi \(x \in \mathbb{R}\)

Đặt \(f\left( x \right) = \left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 4\)

Trường hợp 1: Với \(m =  - 1\) ta có: \(f\left( x \right) = 4 \ge 0\). Do đó, f(x) xác định với mọi giá trị thực của x. Do đó, \(m =  - 1\) thỏa mãn.

Trường hợp 2: \(m \ne  - 1\).

Hàm số \(f\left( x \right) = \left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 4 \ge 0\) với mọi \(x \in \mathbb{R}\)

\( \Leftrightarrow \left\{ \begin{array}{l}m + 1 > 0\\\Delta ' = {\left[ { - \left( {m + 1} \right)} \right]^2} - 4\left( {m + 1} \right) \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m >  - 1\\\left( {m + 1} \right)\left( {m - 3} \right) \le 0\end{array} \right. \Leftrightarrow  - 1 < m \le 3\)

Vậy với \(m \in \left[ { - 1;3} \right]\) thì hàm số \(y = \frac{1}{4}\sqrt {\log \left( {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 5} \right)} \) có tập xác định là \(\mathbb{R}\).

Câu 2 :

Cho hình vuông ABCD. Gọi H, K lần lượt là trung điểm của AB, AD. Trên đường thẳng vuông góc với (ABCD) tại H, lấy điểm S. Chứng minh rằng:

a) \(AC \bot \left( {SHK} \right)\).

b) \(CK \bot \left( {SDH} \right)\).
Phương pháp giải :

+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).

+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Lời giải chi tiết :

a) Vì H, K lần lượt là trung điểm của AB và AD nên HK là đường trung bình của tam giác ABD. Do đó, \(HK//BD\). Mà \(AC \bot BD\) (do ABCD là hình vuông) nên \(AC \bot HK\)

Vì \(AC \bot HK,SH \bot AC\left( {do\;AC \subset \left( {ABCD} \right)} \right) \Rightarrow AC \bot \left( {SHK} \right)\)

b) Gọi I là giao điểm của CK và DH.

Tam giác AHD và tam giác DKC có: \(AH = DK,\widehat {HAD} = \widehat {KDC},AD = DC\)

Do đó, \(\Delta AHD = \Delta DKC\left( {c.g.c} \right) \Rightarrow \widehat {HDA} = \widehat {KCD}\)

Ta có: \(\widehat {DKC} + \widehat {KCD} = {90^0} \Rightarrow \widehat {DKC} + \widehat {HDA} = {90^0}\)

Ta có: \(\widehat {DIK} = {180^0} - \left( {\widehat {DKC} + \widehat {HDA}} \right) = {90^0} \Rightarrow DH \bot CK\)

Mà \(SH \bot \left( {ABCD} \right),CK \subset \left( {ABCD} \right) \Rightarrow SH \bot CK\)

Ta có: \(DH \bot CK,SH \bot CK\), SH và DH nằm trong mặt phẳng (SHD) và cắt nhau tại H nên \(CK \bot \left( {SDH} \right)\).

Câu 3 :

Giải bất phương trình \({\log _2}\left( {x - \sqrt {{x^2} - 1} } \right).{\log _3}\left( {x + \sqrt {{x^2} - 1} } \right) = {\log _6}\left| {x - \sqrt {{x^2} - 1} } \right|\).
Phương pháp giải :

Nếu \(a > 0,a \ne 1\) thì \({\log _a}u\left( x \right) = {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) = v\left( x \right)\end{array} \right.\) (có thể thay \(u\left( x \right) > 0\) bằng \(v\left( x \right) > 0\))

Lời giải chi tiết :

Điều kiện: \(\left\{ \begin{array}{l} - 1 \le x \le 1\\x - \sqrt {{x^2} - 1}  > 0\end{array} \right.\left( * \right)\)

\({\log _2}\left( {x - \sqrt {{x^2} - 1} } \right).{\log _3}\left( {x + \sqrt {{x^2} - 1} } \right) = {\log _6}\left| {x - \sqrt {{x^2} - 1} } \right|\)

\( \Leftrightarrow {\log _2}\left( {x - \sqrt {{x^2} - 1} } \right).{\log _3}\frac{1}{{x - \sqrt {{x^2} - 1} }} = {\log _6}\left( {x - \sqrt {{x^2} - 1} } \right)\)

\( \Leftrightarrow  - {\log _2}\left( {x - \sqrt {{x^2} - 1} } \right).{\log _3}6.{\log _6}\left( {x - \sqrt {{x^2} - 1} } \right) = {\log _6}\left( {x - \sqrt {{x^2} - 1} } \right)\)

\( \Leftrightarrow {\log _6}\left( {x - \sqrt {{x^2} - 1} } \right)\left[ {{{\log }_3}6.{{\log }_2}\left( {x - \sqrt {{x^2} - 1} } \right) + 1} \right] = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}{\log _6}\left( {x - \sqrt {{x^2} - 1} } \right) = 0\;\left( 1 \right)\\{\log _3}6.{\log _2}\left( {x - \sqrt {{x^2} - 1} } \right) + 1 = 0\;\left( 2 \right)\end{array} \right.\)

\(\left( 1 \right) \Leftrightarrow x - \sqrt {{x^2} - 1}  = 1 \Leftrightarrow \sqrt {{x^2} - 1}  = x - 1 \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} - 1 = {\left( {x - 1} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x = 1\end{array} \right. \Leftrightarrow x = 1\left( {tm\left( * \right)} \right)\)

\(\left( 2 \right) \Leftrightarrow {\log _3}6.{\log _2}\left( {x - \sqrt {{x^2} - 1} } \right) =  - 1 \Leftrightarrow {\log _2}\left( {x + \sqrt {{x^2} - 1} } \right) = {\log _6}3\)

\( \Leftrightarrow x + \sqrt {{x^2} - 1}  = {2^{{{\log }_6}3}} \Leftrightarrow \left\{ \begin{array}{l}x \le {2^{{{\log }_6}3}}\\{x^2} - 1 = {\left( {{2^{{{\log }_6}3}} - x} \right)^2}\end{array} \right. \Leftrightarrow x = \frac{1}{2}\left( {{2^{{{\log }_6}3}} + {2^{ - {{\log }_6}3}}} \right)\) (thỏa mãn điều kiện)

Bài liên quan
close

Tiện ích | Blog

Nội dung từ Loigiaihay.Com