Nội dung từ Loigiaihay.Com
Cho tứ diện ABCD có tất cả các cạnh bằng nhau. Gọi M là trung điểm của CD. Góc giữa hai đường thẳng AB và CD bằng:
-
A.
\({30^0}\).
-
B.
\({60^0}\).
-
C.
\({90^0}\).
-
D.
\({45^0}\).
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
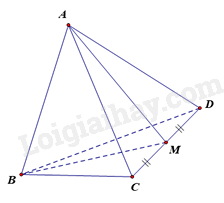
Vì \(AC = AD = CD\) nên tam giác ACD là tam giác đều. Do đó, AM là đường trung tuyến đồng thời là đường cao. Do đó, \(AM \bot CD\)
Vì \(BC = BD = CD\) nên tam giác BCD là tam giác đều. Do đó, BM là đường trung tuyến đồng thời là đường cao. Do đó, \(BM \bot CD\)
Vì \(AM \bot CD\), \(BM \bot CD\), AM, BM cắt nhau tại M và nằm trong mặt phẳng ABM.
Do đó, \(CD \bot \left( {AMB} \right)\). Mà \(AB \subset \left( {ABM} \right) \Rightarrow AB \bot CD\)
Do đó, góc giữa hai đường thẳng AB và CD bằng \({90^0}\).
Đáp án C.
Đáp án : C

Các bài tập cùng chuyên đề
Chọn đáp án đúng.
Với a là số thực khác 0 thì:
Cho biểu thức \(P = \sqrt[6]{x}\) với \(x > 0\). Mệnh đề nào dưới đây là đúng?
Chọn đáp án đúng:
Cho a là số dương, rút gọn biểu thức \(\frac{{\sqrt a .\sqrt[3]{{{a^2}}}}}{{\sqrt[4]{a}}}\) được kết quả là:
Giả sử một lọ nuôi cấy 100 con vi khuẩn lúc ban đầu và số lượng vi khuẩn tăng gấp đôi sau mỗi 2 giờ. Khi đó, số vi khuẩn N sau t giờ là \(N = {100.2^{\frac{t}{2}}}\) (con). Sau 4 giờ 30 phút thì có bao nhiêu con vi khuẩn? (làm tròn đến hàng đơn vị).
Cho hai số thực dương a, b với a khác 1. Số thực c để… được gọi là lôgarit cơ số a của b và kí hiệu là \({\log _a}b\).
Biểu thức phù hợp để điền vào “…” được câu đúng là:
Chọn đáp án đúng.
Với \(a,b > 0,a \ne 1\) thì:
Chọn đáp án đúng:
Với n số thực dương \({b_1},{b_2},..,{b_n},a > 0,a \ne 1\) thì:
Cho x và y là các số dương. Khẳng định nào sau đây là đúng?
Giá trị của biểu thức \(2{\log _5}10 + {\log _{25}}0,25\) là:
Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\) với giá trị nào của a dưới đây?
Hàm số nào dưới đây là không phải hàm số mũ?
Hàm số nào sau đây có tập xác định là \(\mathbb{R}\)?
Hàm số \(y = {\log _{10}}x\) có tập giá trị là:
Cho đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) có đồ thị là hình dưới đây:
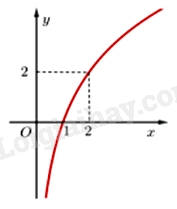
Tìm a.
Có bao nhiêu giá trị nguyên của a để hàm số \(y = {\left( { - {a^2} + 2a + 4} \right)^x}\) đồng biến trên \(\mathbb{R}\)?
Cho bất phương trình \({6^x} > b\). Với giá trị nào của b thì bất phương trình đã cho có tập nghiệm là \(\mathbb{R}\)?
Tập nghiệm của bất phương trình \({\left( {\frac{1}{{\sqrt {15} }}} \right)^x} > \frac{1}{{\sqrt {15} }}\) là
Phương trình \({3^{ - x}} = 4\) có nghiệm là:
Phương trình \({e^{2x}} - 5{e^x} = 0\) có bao nhiêu nghiệm?












