Nội dung từ Loigiaihay.Com
Cho tứ diện ABCD có \(AB = CD = 2a\). Gọi M, N, I lần lượt là trung điểm của BC, AD, AC. Biết rằng \(MN = a\sqrt 3 \). Tính góc giữa hai đường thẳng AB và CD.
-
A.
\({90^0}\).
-
B.
\({60^0}\).
-
C.
\({30^0}\).
-
D.
\({70^0}\).
+ Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b; kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\).
+ Góc giữa hai đường thẳng không vượt quá \({90^0}\).
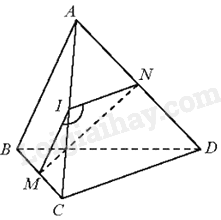
Vì IM là đường trung bình của tam giác ABC nên IM//AB và \(IM = \frac{{AB}}{2} = a\)
Vì IN là đường trung bình của tam giác ADC nên IN//CD và \(IN = \frac{{CD}}{2} = a\)
Do đó, \(\left( {AB,CD} \right) = \left( {IM,IN} \right)\)
Áp dụng định lí côsin vào tam giác MNI ta có:
\(M{N^2} = I{M^2} + I{N^2} - 2IM.IN.\cos \widehat {MIN} \Rightarrow 3{a^2} = {a^2} + {a^2} - 2a.a.\cos \widehat {MIN} \Rightarrow \cos \widehat {MIN} = \frac{{ - 1}}{2} \Rightarrow \widehat {MIN} = {120^0}\)
Suy ra: \(\left( {AB,CD} \right) = \left( {IM,IN} \right) = {180^0} - \widehat {MIN} = {180^0} - {120^0} = {60^0}\)
Đáp án B.
Đáp án : B

Các bài tập cùng chuyên đề
Chọn đáp án đúng.
Với a là số thực khác 0 thì:
Cho biểu thức \(P = \sqrt[6]{x}\) với \(x > 0\). Mệnh đề nào dưới đây là đúng?
Chọn đáp án đúng:
Cho a là số dương, rút gọn biểu thức \(\frac{{\sqrt a .\sqrt[3]{{{a^2}}}}}{{\sqrt[4]{a}}}\) được kết quả là:
Giả sử một lọ nuôi cấy 100 con vi khuẩn lúc ban đầu và số lượng vi khuẩn tăng gấp đôi sau mỗi 2 giờ. Khi đó, số vi khuẩn N sau t giờ là \(N = {100.2^{\frac{t}{2}}}\) (con). Sau 4 giờ 30 phút thì có bao nhiêu con vi khuẩn? (làm tròn đến hàng đơn vị).
Cho hai số thực dương a, b với a khác 1. Số thực c để… được gọi là lôgarit cơ số a của b và kí hiệu là \({\log _a}b\).
Biểu thức phù hợp để điền vào “…” được câu đúng là:
Chọn đáp án đúng.
Với \(a,b > 0,a \ne 1\) thì:
Chọn đáp án đúng:
Với n số thực dương \({b_1},{b_2},..,{b_n},a > 0,a \ne 1\) thì:
Cho x và y là các số dương. Khẳng định nào sau đây là đúng?
Giá trị của biểu thức \(2{\log _5}10 + {\log _{25}}0,25\) là:
Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\) với giá trị nào của a dưới đây?
Hàm số nào dưới đây là không phải hàm số mũ?
Hàm số nào sau đây có tập xác định là \(\mathbb{R}\)?
Hàm số \(y = {\log _{10}}x\) có tập giá trị là:
Cho đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) có đồ thị là hình dưới đây:
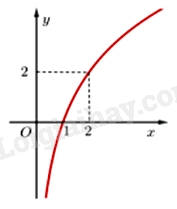
Tìm a.
Có bao nhiêu giá trị nguyên của a để hàm số \(y = {\left( { - {a^2} + 2a + 4} \right)^x}\) đồng biến trên \(\mathbb{R}\)?
Cho bất phương trình \({6^x} > b\). Với giá trị nào của b thì bất phương trình đã cho có tập nghiệm là \(\mathbb{R}\)?
Tập nghiệm của bất phương trình \({\left( {\frac{1}{{\sqrt {15} }}} \right)^x} > \frac{1}{{\sqrt {15} }}\) là
Phương trình \({3^{ - x}} = 4\) có nghiệm là:
Phương trình \({e^{2x}} - 5{e^x} = 0\) có bao nhiêu nghiệm?












