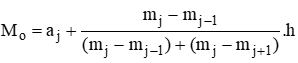Đề cương ôn tập học kì 1 Toán 11 - Chân trời sáng tạoTải vềA. Nội dung ôn tập Hàm số lượng giác và phương trình lượng giác 1. Góc lượng giác 2. Giá trị lượng giác của một góc lượng giác 3. Các công thức lượng giác 4. Hàm số lượng giác và đồ thị 5. Phương trình lượng giác cơ bản A. Nội dung ôn tậpHàm số lượng giác và phương trình lượng giác1. Góc lượng giác 2. Giá trị lượng giác của một góc lượng giác 3. Các công thức lượng giác 4. Hàm số lượng giác và đồ thị 5. Phương trình lượng giác cơ bản Dãy số. Cấp số cộng. Cấp số nhân1. Dãy số 2. Cấp số cộng 3. Cấp số nhân Giới hạn. Hàm số liên tục1. Giới hạn của dãy số 2. Giới hạn của hàm số 3. Hàm số liên tục Đường thẳng và mặt phẳng. Quan hệ song song trong không gian1. Điểm, đường thẳng và mặt phẳng trong không gian 2. Hai đường thẳng song song 3. Đường thẳng và mặt phẳng song song 4. Hai mặt phẳng song song 5. Phép chiếu song song Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm1. Số trung bình và mốt của mẫu số liệu ghép nhóm 2. Trung vị và tứ phân vị của mẫu số liệu ghép nhóm
B. Bài tậpĐề bàiPhần I: Trắc nghiệm nhiều phương án lựa chọnCâu 1. Tập xác định của hàm số y = tanx là A. \(\mathbb{R}\backslash \{ 0\} \) B. \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\) C. \(\mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\) D. \(\mathbb{R}\backslash \left\{ {\frac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\) Câu 2. Số nghiệm thuộc đoạn \([ - \pi ;\pi ]\) của phương trình \(\cos \left( {2x - \frac{\pi }{2}} \right) = 1\) là A. 1 B. 2 C. 3 D. 4 Câu 3. Cho dãy \(\left( {{u_n}} \right)\) với \(\left( {{u_n}} \right) = \frac{{{{( - 1)}^{n - 1}}}}{{n + 1}}\). Số hạng thứ 9 của dãy là A. \({u_9} = \frac{1}{{10}}\) B. \({u_9} = - \frac{1}{{10}}\) C. \({u_9} = \frac{{ - 1}}{9}\) D. \({u_9} = \frac{1}{9}\) Câu 4. Trong các dãy số sau, dãy số nào là dãy số tăng? A. \({u_n} = {n^2}\) B. \({u_n} = \frac{1}{{\sqrt n }}\) C. \({u_n} = 3 - 2n\) D. \({u_n} = - 2{n^2} + 3n + 1\) Câu 5. Cho cấp số cộng có các số hạng lần lượt là -4, 1, x. Khi đó, giá trị của x bằng A. x = 9 B. x = 4 C. x = 7 D. x = 6 Câu 6. Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({S_2} = 4\), \({S_3} = 13\). Biết \({u_2} < 0\), giá trị của \({S_5}\) bằng A. 11 B. 2 C. \(\frac{{35}}{{16}}\) D. \(\frac{{181}}{{16}}\) Câu 7. Trong các mệnh đề sau, mệnh đề nào sai? A. Nếu \(\lim {u_n} = + \infty \) và \(\lim {v_n} = a > 0\) thì \(\lim \left( {{u_n}{v_n}} \right) = + \infty \) B. Nếu \(\lim {u_n} = a \ne 0\) và \(\lim {v_n} = \pm \infty \) thì \(\lim \left( {\frac{{{u_n}}}{{{v_n}}}} \right) = 0\) C. Nếu \(\lim {u_n} = a > 0\) và \(\lim {v_n} = 0\) thì \(\lim \left( {\frac{{{u_n}}}{{{v_n}}}} \right) = + \infty \) D. Nếu \(\lim {u_n} = a < 0\) và \(\lim {v_n} = 0\) và \({v_n} > 0\) với mọi n thì \(\lim \left( {\frac{{{u_n}}}{{{v_n}}}} \right) = - \infty \) Câu 8. Biết giới hạn \(\lim \frac{{3 - 2n}}{{5n + 1}} = \frac{a}{b}\) trong đó \(a,b \in \mathbb{Z}\) và \(\frac{a}{b}\) tối giản. Tính a.b. \(\) A. 6 B. 3 C. -10 D. 15 Câu 9. Cho hàm số \(y = \frac{{{x^2} - 9}}{{{x^2} - 3x}}\). Khẳng định nào dưới đây đúng? A. Hàm số có 2 điểm gián đoạn là x = -3, x = 3 B. Hàm số chỉ có 1 điểm gián đoạn là x = 0 C. Hàm số chỉ có 1 điểm gián đoạn là x = 3 D. Hàm số có 2 điểm gián đoạn là x = 0, x = 3 Câu 10. Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{2{x^2} + 3x - 14}}{{4 - {x^2}}}\\a\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x \ne 2\\x = 2\end{array}\). Với giá trị nào của a thì hàm số liên tục tại x = 2? A. \( - \frac{{11}}{4}\) B. \(\frac{{11}}{4}\) C. \(\frac{{11}}{2}\) D. \( - \frac{{11}}{2}\) Câu 11. Khẳng định nào sau đây đúng? A. Hai đường thẳng chéo nhau thì không có điểm chung B. Hai đường thẳng không có điểm chung thì song song C. Hai đường thẳng nằm trong hai mặt phẳng phân biệt thì chéo nhau D. Hai đường thẳng không có điểm chung thì chéo nhau Câu 12. Cho hình chóp S.ABCD có O là giao điểm của AC và BD. Gọi M, I lần lượt là trung điểm của BD, SD. Điểm nào dưới đây thuộc mặt phẳng (SAO)? A. Điểm B B. Điểm M C. Điểm I D. Điểm C Câu 13. Cho hình chóp S.ABCD có ABCD là hình bình hành, I là trung điểm SB. J, K là điểm thuộc BC, AD sao cho \(\frac{{BJ}}{{BC}} = \frac{{DK}}{{DA}} = \frac{1}{3}\), M là trung điểm SA. Hỏi SC song song với mặt phẳng nào sau đây? A. (MJK) B. (IJK) C. (IBK) D. (IJA) Câu 14. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng).
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [7;9) B. [9;11) C. [11;13) D. [13;15) Câu 15. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau.
Nhóm chứa trung vị là A. [30;45) B. [15;30) C. [45,60) D. [60;75) Phần II: Trắc nghiệm đúng saiCâu 16. Cho phương trình lượng giác \(\sin x = m,m \in \mathbb{R}\). Khi đó: a) \(\cos 2x = 2{m^2} - 1\). b) Nếu \(m = \frac{2}{3}\) thì \(\sin x = m\) có hai nghiệm phân biệt \(x \in [0;3\pi ]\). c) Phương trình vô nghiệm khi và chỉ khi m > 1. d) Nếu \(m = \frac{1}{2}\) thì phương trình có nghiệm là \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \frac{{5\pi }}{6} + k2\pi }\end{array}} \right.\) với \(k \in \mathbb{Z}\). Câu 17. Cho dãy số \(({u_n})\) biết \({u_n} = {2^n}\). Khi đó: \[\] a) Dãy số \(({u_n})\) là dãy số tăng. b) Dãy số \(({u_n})\) là dãy số bị chặn. c) \({u_8} = 64\). d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\). Câu 18. Kết quả khảo sát cân nặng của 25 quả cam ở mỗi lô hàng A, B được cho ở bảng sau:
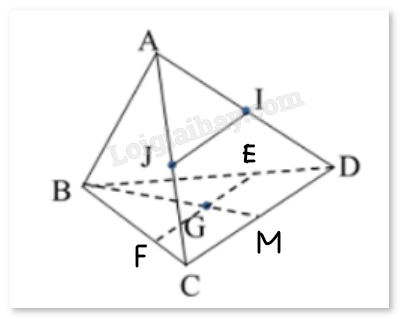
a) Giá trị đại diện của nhóm [150;155) bằng 152,5 b) Nhóm chứa mốt của mẫu số liệu ở lô hàng A là [155;160) c) Nhóm chứa mốt của mẫu số liệu ở lô hàng B là [160;165) d) Theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A Câu 19. Cho \({u_n} = \frac{{{7^n} + {2^{2n - 1}} + {3^{n + 1}}}}{{{7^{n + 1}} + {5^{n - 1}}}}\). Biết \(\lim {u_n} = \frac{a}{b}\) với \(a,b \in \mathbb{Z}\), \(\frac{a}{b}\) tối giản. Khi đó: a) a + b = 8. b) a – b = -7 c) Bộ ba số a; b; 13 tạo thành một cấp số cộng có công sai d = 7. d) Bộ ba số a; b; 49 tạo thành một cấp số nhân có công bội q = 7. Câu 20. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Mặt phẳng (P) qua BD và song song với SA. Khi đó a) Giao tuyến của hai mặt phẳng (SAB) và (SAD) là SO. b) SO thuộc mặt phẳng (SBD). c) Gọi I là giao điểm của SC và (P). Khi đó OI//SA. d) Thiết diện giữa (P) và hình chóp là hình bình hành. Phần III: Trắc nghiệm trả lời ngắnCâu 21. Cho vận tốc v (cm/s) của một con lắc đơn theo thời gian t (giây) được xác định bởi công thức \(v = - 4\sin \left( {1,5t + \frac{\pi }{4}} \right)\) với \(0 \le t \le 2\). Xác định thời điểm vận tốc con lắc bằng 2 cm/s (Làm tròn kết quả đến hàng phần mười)? Câu 22. Khán đài D của một sân vận động có 20 hàng ghế xếp theo hình quạt. hàng thứ nhất có 13 ghế, hàng thứ hai có 16 ghế, hàng thứ ba có 19 ghế,…, cứ thế tiếp tục cho đến hàng cuối cùng. Số ghế ở hàng cuối cùng là? Câu 23. Để trang hoàng cho căn hộ của mình, chú chuột Mickey quyết định tô màu một miếng bìa hình
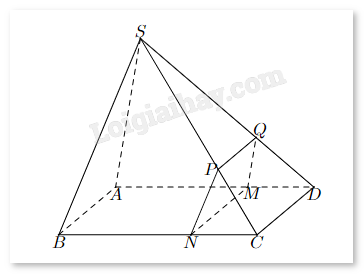
Câu 24. Tính giới hạn \(\mathop {\lim }\limits_{x \to 0} \frac{{{{(x + 3)}^3} - 27}}{x}\). Câu 25. Cho tứ diện ABCD. Điểm I và J theo thức tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GIJ) và (BCD) cắt BD tại E, cắt BC tại F. Tính tỉ số \(\frac{{IJ}}{{EF}}\) (Viết dưới dạng số thập phân)? Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và một điểm M nằm trên cạnh AD (giữa A và D) sao cho AD = 3MD. Một mặt phẳng \((\alpha )\) đi qua M, song song với CD và SA, cắt BC, SC, SD lần lượt tại N, P, Q. Với cạnh CD = 9 (cm) thì độ dài đoạn PQ là bao nhiêu?
Câu 27. Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:
Tìm tứ phân vị thứ nhất của mẫu số liệu. Câu 28. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A.
Số học sinh có chiều cao bao nhiêu cm là nhiều nhất (làm tròn đến hàng đơn vị)? Đáp ánPhần I: Trắc nghiệm nhiều phương án lựa chọn
Phần II: Trắc nghiệm đúng saiCâu 16. Cho phương trình lượng giác \(\sin x = m\), \(m \in \mathbb{R}\). Khi đó: a) \(\cos 2x = 2{m^2} - 1\). b) Nếu \(m = \frac{2}{3}\) thì \(\sin x = m\) có hai nghiệm phân biệt \(x \in [0;3\pi ]\). c) Phương trình vô nghiệm khi và chỉ khi m > 1. d) Nếu \(m = \frac{1}{2}\) thì phương trình có nghiệm là \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \frac{{5\pi }}{6} + k2\pi }\end{array}} \right.\) với \(k \in \mathbb{Z}\). Phương pháp giải: Giải phương trình lượng giác \(\sin x = a\): - Nếu \(\left| a \right| > 1\) thì phương trình vô nghiệm. - Nếu \(\left| a \right| \le 1\) thì chọn cung \(\alpha \) sao cho \(\sin \alpha = a\). Khi đó phương trình trở thành: \(\sin x = \sin \alpha \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha + k2\pi }\\{x = \pi - \alpha + k2\pi }\end{array}} \right.\) với \(k \in \mathbb{Z}\). Lời giải chi tiết: a) Sai. \(\cos 2x = 1 - 2{\sin ^2}x = 1 - 2{m^2}\). b) Sai. \(\sin x = \frac{{\sqrt 3 }}{2} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{3} + k2\pi }\\{x = \frac{{2\pi }}{3} + k2\pi }\end{array}} \right.\) Vì \(x \in [0;3\pi ]\) nên \(x = \frac{\pi }{3}\); \(x = \frac{{7\pi }}{3}\); \(x = \frac{{2\pi }}{3}\); \(x = \frac{{8\pi }}{3}\). Vậy phương trình có bốn nghiệm phân biệt. c) Sai. Phương trình vô nghiệm khi và chỉ khi m > 1 hoặc m < -1. d) Đúng. \(\sin x = \frac{1}{2} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \pi - \frac{\pi }{6} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \frac{{5\pi }}{6} + k2\pi }\end{array}} \right.\) Câu 17. Cho dãy số \(({u_n})\) biết \({u_n} = {2^n}\). Khi đó: \(\) a) Dãy số \(({u_n})\) là dãy số tăng. b) Dãy số \(({u_n})\) là dãy số bị chặn. c) \({u_8} = 64\). d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\). Phương pháp giải: a) Dãy số \(({u_n})\) là dãy số giảm nếu \({u_n} > {u_{n + 1}}\). Dãy số \(({u_n})\) là dãy số tăng nếu \({u_n} < {u_{n + 1}}\). b) Dãy số \(({u_n})\) là dãy số bị chặn nếu \(({u_n})\) vừa bị chặn trên vừa bị chặn dưới, tức tồn tại số thực dương M sao cho \(\left| {{u_n}} \right| < M\) \(\forall n \in M\). c) Tính \({u_8}\) bằng công thức \({u_n} = {2^n}\). d) Thay n + 2 vào n trong công thức số hạng tổng quát \({u_n} = {2^n}\). Lời giải chi tiết: a) Đúng. \({u_{n + 1}} - {u_n} = {2^{n + 1}} - {2^n} = {2^n}.2 - {2^n} = {2^n}(2 - 1) = {2^n} > 0\) với mọi n. Vậy dãy số là dãy tăng. b) Sai. Dãy không bị chặn trên vì không có giá trị M nào để \({2^n} < M\) với mọi n. Vậy dãy số không bị chặn. c) Sai. \({u_8} = {2^8} = 256\). d) Sai. \({u_{n + 2}} = {2^{n + 2}} = {4.2^n}\). Câu 18. Kết quả khảo sát cân nặng của 25 quả cam ở mỗi lô hàng A, B được cho ở bảng sau:
a) Giá trị đại diện của nhóm [150;155) bằng 152,5 b) Nhóm chứa mốt của mẫu số liệu ở lô hàng A là [155;160) c) Nhóm chứa mốt của mẫu số liệu ở lô hàng B là [160;165) d) Theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A Phương pháp giải: a) Giá trị đại diện nhóm \([{a_m};{a_n})\) là: \(\frac{{{a_m} + {a_n}}}{2}\). b) Nhóm chứa mốt có tần số cao nhất. c) Nhóm chứa mốt có tần số cao nhất. d) Tính cân nặng trung bình của mỗi lô hàng rồi so sánh. Lời giải chi tiết: a) Đúng. Giá trị đại diện nhóm [150;155) là \(\frac{{150 + 155}}{2} = 152,5\). b) Sai. Nhóm chứa mốt của mẫu số liệu ở lô hàng A là [160;165) vì có tần số cao nhất là 12. c) Sai. Nhóm chứa mốt của mẫu số liệu ở lô hàng B là [165;170) vì có tần số cao nhất là 10. d) Đúng. Bảng thống kê số lượng cam theo giá trị đại diện:
Cân nặng trung bình của mỗi quả cam ở lô A là: \(\overline {{x_A}} = \frac{{152,5.2 + 157,5.6 + 162,5.12 + 167,5.4 + 172,5.1}}{{25}} = 161,7\) (gam). Cân nặng trung bình của mỗi quả cam ở lô B là: \(\overline {{x_B}} = \frac{{152,5.1 + 157,5.3 + 162,5.7 + 167,5.10 + 172,5.4}}{{25}} = 165,1\) (gam). Thấy \(\overline {{x_A}} < \overline {{x_B}} \). Vậy nếu so sánh theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A. Câu 19. Cho \({u_n} = \frac{{{7^n} + {2^{2n - 1}} + {3^{n + 1}}}}{{{7^{n + 1}} + {5^{n - 1}}}}\). Biết \(\lim {u_n} = \frac{a}{b}\) với \(a,b \in \mathbb{Z}\), \(\frac{a}{b}\) tối giản. Khi đó: a) a + b = 8. b) a – b = -7 c) Bộ ba số a; b; 13 tạo thành một cấp số cộng có công sai d = 7. d) Bộ ba số a; b; 49 tạo thành một cấp số nhân có công bội q = 7. Phương pháp giải: Chia cả tử và mẫu của \({u_n}\) cho \({7^n}\). Áp dụng công thức \(\lim {q^n} = 0\) khi \(\left| q \right| < 1\). Lời giải chi tiết: Ta có \(\lim {u_n} = \lim \frac{{{7^n} + {2^{2n - 1}} + {3^{n + 1}}}}{{{7^{n + 1}} + {5^{n - 1}}}} = \lim \frac{{{7^n} + {4^n}{{.2}^{ - 1}} + {3^n}.3}}{{{7^n}.7 + {5^n}{{.5}^{ - 1}}}}\) \( = \lim \frac{{1 + {{\left( {\frac{4}{7}} \right)}^n}{{.2}^{ - 1}} + {{\left( {\frac{3}{7}} \right)}^n}.3}}{{1.7 + {{\left( {\frac{5}{7}} \right)}^n}{{.5}^{ - 1}}}} = \frac{{1 + 0 + 0}}{{7 + 0}} = \frac{1}{7}\). Vậy \(\frac{a}{b} = \frac{1}{7}\) hay a = 1, b = 7. a) Đúng. a + b = 1 + 7 = 8. b) Sai. a – b = 1 – 6 = -6. c) Sai. 1; 7; 13 tạo thành cấp số cộng có công sai bằng d = 6. d) Đúng. 1; 7; 49 tạo thành cấp số nhân có công bội q = 7. Câu 20. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Mặt phẳng (P) qua BD và song song với SA. Khi đó a) Giao tuyến của hai mặt phẳng (SAB) và (SAD) là SO. b) SO thuộc mặt phẳng (SBD). c) Gọi I là giao điểm của SC và (P). Khi đó OI//SA. d) Thiết diện giữa (P) và hình chóp là hình bình hành. Phương pháp giải: Sử dụng các định lý về đường thẳng song song với mặt phẳng, cách tìm giao tuyến, thiết diện của hai mặt phẳng. Lời giải chi tiết:
a) Sai. Giao tuyến của hai mặt phẳng (SAB) và (SAD) là SA. b) Đúng. SO thuộc mặt phẳng (SBD) vì cả \(S \in (SBD)\), \(O \in BD \subset (SBD)\). c) Đúng. Có \(OI \subset (P)\) mà SA//(P) nên SA không cắt đường thẳng nào trong (P), tức OI//SA (do OI, SA cùng thuộc mặt phẳng (SAC)). d) Sai. Thiết diện là tam giác BID. Phần III: Trắc nghiệm trả lời ngắnCâu 21. Cho vận tốc v (cm/s) của một con lắc đơn theo thời gian t (giây) được xác định bởi công thức \(v = - 4\sin \left( {1,5t + \frac{\pi }{4}} \right)\) với \(0 \le t \le 2\). Xác định thời điểm vận tốc con lắc bằng 2 cm/s (Làm tròn kết quả đến hàng phần mười)? Phương pháp giải: Thay \(v = 2\) vào công thức \(v = - 4\sin \left( {1,5t + \frac{\pi }{4}} \right)\) và tìm t. Lời giải chi tiết: \(2 = - 4\sin \left( {1,5t + \frac{\pi }{4}} \right) \Leftrightarrow - \frac{1}{2} = \sin \left( {1,5t + \frac{\pi }{4}} \right) \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{1,5t + \frac{\pi }{4} = - \frac{\pi }{6} + k2\pi }\\{1,5t + \frac{\pi }{4} = \frac{{7\pi }}{3} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = - \frac{\pi }{3} + k\frac{{4\pi }}{3}}\\{t = \frac{{5\pi }}{9} + k\frac{{4\pi }}{3}}\end{array}} \right.\) với \(k \in \mathbb{Z}\). Vì \(0 \le t \le 2\) nên chỉ có 1 giá trị của t thỏa mãn là \(t = \frac{{5\pi }}{9} \approx 1,7\). Đáp án: 1,7. Câu 22. Khán đài D của một sân vận động có 20 hàng ghế xếp theo hình quạt. hàng thứ nhất có 13 ghế, hàng thứ hai có 16 ghế, hàng thứ ba có 19 ghế,…, cứ thế tiếp tục cho đến hàng cuối cùng. Số ghế ở hàng cuối cùng là? Phương pháp giải: Số ghế mỗi hàng ở khán đài lập thành một cấp số cộng với 20 hàng tương đương 20 số hạng. Tìm số hạng đầu, công sai từ đó tìm số hạng thứ 20. Lời giải chi tiết: Số ghế mỗi hàng ở khán đài lập thành một cấp số cộng với 20 hàng tương đương 20 số hạng. Ta có: \({u_1} = 13,{u_2} = 16,{u_3} = 19\) nên công sai bằng \(d = {u_2} - {u_1} = {u_3} - {u_2} = 3\). Số ghế hàng cuối cùng là: \({u_{20}} = 13 + (20 - 1).3 = 70\). Đáp án: 70. Câu 23. Để trang hoàng cho căn hộ của mình, chú chuột Mickey quyết định tô màu một miếng bìa hình
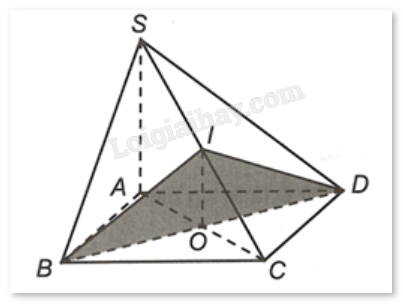
Phương pháp giải: Áp dụng công thức tính tổng cấp số nhân lùi vô hạn: \({S_n} = \frac{{{u_1}}}{{1 - q}}\). Lời giải chi tiết: Gọi \({a_1},{a_2},...,{a_n}\) lần lượt là cạnh các hình vuông được tô màu theo thứ tự từ lớn đến nhỏ. Ta có \({a_1} = \frac{1}{2}\), \({a_2} = \frac{1}{4} = {\left( {\frac{1}{2}} \right)^2}\), \({a_3} = \frac{1}{8} = {\left( {\frac{1}{2}} \right)^3}\),…, \({a_n} = {\left( {\frac{1}{2}} \right)^n}\). Gọi \({u_1},{u_2},...,{u_n}\) lần lượt là diện tích các hình vuông ứng với cạnh \({a_1},{a_2},...,{a_n}\). Khi đó \({u_n} = {\left( {\frac{1}{2}} \right)^{2n}} = {\left( {\frac{1}{4}} \right)^n}\) là số hạng tổng quát của cấp số nhân có \({u_1} = \frac{1}{4}\), \(q = \frac{1}{4}\). Có \({S_n} = {u_1} + {u_2} + ... + {u_n}\) là tổng của cấp số nhân lùi vô hạn. Vậy diện tích cần tô màu là \({S_n} = \frac{{{u_1}}}{{1 - q}} = \frac{{\frac{1}{4}}}{{1 - \frac{1}{4}}} = \frac{1}{3} \approx 0,33\). Đáp án: 0,33. Câu 24. Tính giới hạn \(\mathop {\lim }\limits_{x \to 0} \frac{{{{(x + 3)}^3} - 27}}{x}\). Phương pháp giải: Sử dụng hằng đẳng thức \({a^3} - {b^3} = (a - b)({a^2} + ab + {b^2})\). Lời giải chi tiết: \(\mathop {\lim }\limits_{x \to 0} \frac{{{{(x + 3)}^3} - 27}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{{{(x + 3)}^3} - {3^3}}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{(x + 3 - 3)\left[ {{{(x + 3)}^2} + (x + 3).3 + 9} \right]}}{x}\) \( = \mathop {\lim }\limits_{x \to 0} \frac{{x\left[ {{x^2} + 6x + 9 + 3x + 9 + 9} \right]}}{x} = \mathop {\lim }\limits_{x \to 0} ({x^2} + 9x + 27) = {0^2} + 9.0 + 27 = 27\). Đáp án: 27. Câu 25. Cho tứ diện ABCD. Điểm I và J theo thức tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GIJ) và (BCD) cắt BD tại E, cắt BC tại F. Tính tỉ số \(\frac{{IJ}}{{EF}}\) (Viết dưới dạng số thập phân)? Phương pháp giải: Sử dụng định lý giao tuyến của ba mặt phẳng, định lý Thales. Lời giải chi tiết:
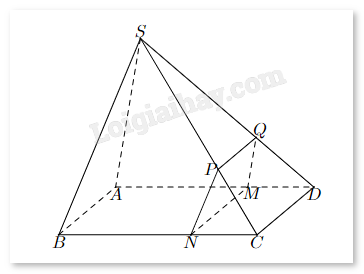
Gọi \(BG \cap CD = \{ M\} \), khi đó M là trung điểm của CD (vì G là trọng tâm \(\Delta BCD\)). Xét \(\Delta ACD\) có IJ//CD suy ra \(\frac{{AI}}{{AD}} = \frac{{AJ}}{{AC}} = \frac{1}{2}\) (I và J theo thức tự là trung điểm của AD và AC). Từ đó dễ dàng chứng minh \(\Delta AIJ\)ᔕ\(\Delta ADC\), suy ra \(\frac{{IJ}}{{CD}} = \frac{1}{2}\), tức \(IJ = \frac{1}{2}CD\) (1) Ta có: \(\left\{ {\begin{array}{*{20}{c}}{CD = (ACD) \cap (BCD)}\\{IJ = (ACD) \cap (IJG)}\\{EF = (IJG) \cap (BCD)}\\{IJ/CD}\end{array}} \right.\). Theo định lý về giao tuyến của ba mặt phẳng, ta được: EF//CD//IJ. Vì \(\left\{ {\begin{array}{*{20}{c}}{EF = (IJG) \cap (BCD)}\\\begin{array}{l}G \in (IJG)\\G \in (BCD)\end{array}\end{array}} \right.\) nên E, G, F thẳng hàng. Xét \(\Delta BCM\) có FG//CM (vì EF//CD) suy ra \(\frac{{BF}}{{BC}} = \frac{{BG}}{{BM}} = \frac{2}{3}\) (vì G là trọng tâm \(\Delta BCD\)). Xét \(\Delta BCD\) có EF//CD suy ra \(\frac{{BF}}{{BC}} = \frac{{BE}}{{BD}} = \frac{2}{3}\). Từ đó dễ dàng chứng minh \(\Delta BEF\)ᔕ\(\Delta BDC\), suy ra \(\frac{{EF}}{{CD}} = \frac{2}{3}\), tức \(EF = \frac{2}{3}CD\) (2) Từ (1) và (2) suy ra \(\frac{{IJ}}{{EF}} = \frac{{\frac{1}{2}CD}}{{\frac{2}{3}CD}} = \frac{3}{4} = 0,75\). Đáp án: 0,75. Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và một điểm M nằm trên cạnh AD (giữa A và D) sao cho AD = 3MD. Một mặt phẳng \((\alpha )\) đi qua M, song song với CD và SA, cắt BC, SC, SD lần lượt tại N, P, Q. Với cạnh CD = 9 (cm) thì độ dài đoạn PQ là bao nhiêu?
Phương pháp giải: Sử dụng định lý giao tuyến của ba mặt phẳng, định lý Thales. Lời giải chi tiết: \(SA//(\alpha )\) nên SA không cắt \(QM \subset (\alpha )\). Mặt khác, SA và QM cùng thuộc mặt phẳng (SAD) nên SA//QM. Xét \(\Delta SAD\)\(\Delta SAD\) có QM//SA: \(\frac{{MD}}{{AD}} = \frac{{QD}}{{SD}} = \frac{1}{3}\), suy ra \(\frac{{SQ}}{{SD}} = \frac{2}{3}\). Ta có: \(\left\{ {\begin{array}{*{20}{c}}{MN = (\alpha ) \cap (ABCD)}\\{CD = (ICD) \cap (ABCD)}\\{PQ = (\alpha ) \cap (ICD)}\\{MN//CD}\end{array}} \right.\). Theo định lý về giao tuyến của ba mặt phẳng, ta được: PQ//CD//MN. Xét \(\Delta SCD\) có PQ//CD: \(\frac{{PQ}}{{CD}} = \frac{{SQ}}{{SD}} = \frac{2}{3}\), suy ra \(PQ = \frac{2}{3}CD = \frac{2}{3}.9 = 6\). Đáp án: 6. Câu 27. Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:
Tìm tứ phân vị thứ nhất của mẫu số liệu. Phương pháp giải:
Lời giải chi tiết: Tổng số viên pin là: 10 + 20 + 35 +15 + 5 = 85. Gọi \({x_1};{x_2};{x_3};...;{x_{85}}\) lần lượt là số viên pin theo thứ tự không giảm. Tứ phân vị thứ nhất của dãy số liệu là \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right)\) thuộc nhóm [0,95; 1,0) nên tứ phân vị thứ nhất của mẫu số liệu là \({Q_1} = 0,95 + \frac{{\frac{{85}}{4} - 10}}{{20}}\left( {1,0 - 0,95} \right) = 0,98\). Đáp án: 0,98. Câu 28. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A.
Số học sinh có chiều cao bao nhiêu cm là nhiều nhất (làm tròn đến hàng đơn vị)? Phương pháp giải: Tìm mốt của mẫu số liệu. Bước 1: Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: [aj; aj+1). Bước 2: Mốt được xác định là
trong đó mj là tần số của nhóm j (quy ước mo = mk+1 = 0) và h là độ dài của nhóm. Lời giải chi tiết: Tần số lớn nhất là 14 nên nhóm chứa mốt là nhóm [150;155). Ta có \({M_o} = 150 + \frac{{14 - 7}}{{(14 - 7) + (14 - 10)}}(155 - 150) \approx 153\). Vậy số học sinh có chiều cao khoảng 153 cm là nhiều nhất. Đáp án: 153.  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
