Đề thi giữa kì 1 Toán 8 Kết nối tri thức - Đề số 8Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau: Câu 1: Hệ số của đơn thức $5{{x}^{2}}y.left( -frac{2}{5} right){{y}^{2}}z$ là:Đề bài
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Hệ số của đơn thức \(5{x^2}y.\left( { - \frac{2}{5}} \right){y^2}z\) là:
Câu 2 :
Tổng của các đơn thức \(3{x^2}{y^3}; - 5{x^2}{y^3}\) và \({x^2}{y^3}\) là:
Câu 3 :
Bậc của đa thức \(5{x^2}y - {x^4} + 4xy + {x^4}\) là:
Câu 4 :
Rút gọn biểu thức \(A = 2{x^2}\left( {{y^3} - {x^3}} \right) - {y^3}\left( {2{x^2} - y} \right)\), ta được kết quả là:
Câu 5 :
Có bao nhiêu số nguyên dương m thỏa mãn đa thức \(A = 4{x^2}{y^3} + 3{x^3}{y^2}\) chia hết cho đơn thức \(B = 2{x^2}{y^m}\)?
Câu 6 :
Biểu thức \(\left( {3x + y} \right)\left( {y - 3x} \right)\) bằng
Câu 7 :
Điền vào chỗ trống: \(\left( {3x + y} \right)\left( {9{x^2} + ... + {y^2}} \right) = 27{x^3} + {y^3}\)
Câu 8 :
Phân tích đa thức \({\left( {x - 4} \right)^2} + \left( {x - 4} \right)\) thành nhân tử, ta được:
Câu 9 :
Cho tứ giác ABCD. Chọn khẳng định sai trong các khẳng định sau:
Câu 10 :
Trong hình thang có hai góc tù thì
Câu 11 :
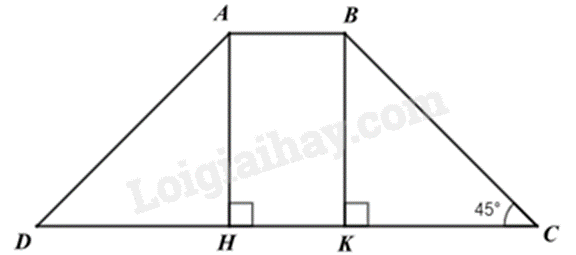
Cho hình thang cân ABCD có đáy nhỏ AB = 3cm, đường cao AH = 5cm và \(\widehat {BCD} = 45^\circ \). Độ dài đáy lớn CD là:
Câu 12 :
Phát biểu nào sau đây là đúng?
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1 :
Hệ số của đơn thức \(5{x^2}y.\left( { - \frac{2}{5}} \right){y^2}z\) là:
Đáp án : B Phương pháp giải :
Thu gọn đa thức để tìm hệ số. Lời giải chi tiết :
Ta có: \(5{x^2}y.\left( { - \frac{2}{5}} \right){y^2}z = \left( {5.\frac{{ - 2}}{5}} \right){x^2}.\left( {y.{y^2}} \right).z = - 2{x^2}{y^3}z\). Đơn thức này có hệ số là -2. Đáp án B.
Câu 2 :
Tổng của các đơn thức \(3{x^2}{y^3}; - 5{x^2}{y^3}\) và \({x^2}{y^3}\) là:
Đáp án : B Phương pháp giải :
Thực hiện cộng các đơn thức đồng dạng. Lời giải chi tiết :
Ta có: \(3{x^2}{y^3} + \left( { - 5{x^2}{y^3}} \right) + {x^2}{y^3} = \left( {3 - 5 + 1} \right){x^2}{y^3} = - {x^2}{y^3}\). Đáp án B.
Câu 3 :
Bậc của đa thức \(5{x^2}y - {x^4} + 4xy + {x^4}\) là:
Đáp án : A Phương pháp giải :
Thu gọn đa thức rồi tìm bậc của đa thức thu gọn đó. Lời giải chi tiết :
Ta có: \(5{x^2}y - {x^4} + 4xy + {x^4} = 5{x^2}y + 4xy\) Đa thức này có bậc là 3. Đáp án A.
Câu 4 :
Rút gọn biểu thức \(A = 2{x^2}\left( {{y^3} - {x^3}} \right) - {y^3}\left( {2{x^2} - y} \right)\), ta được kết quả là:
Đáp án : A Phương pháp giải :
Thực hiện nhân đơn thức với đa thức sau đó thu gọn đa thức nhận được. Lời giải chi tiết :
Ta có: \(\begin{array}{l}A = 2{x^2}\left( {{y^3} - {x^3}} \right) - {y^3}\left( {2{x^2} - y} \right)\\ = 2{x^2}{y^3} - 2{x^5} - 2{x^2}{y^3} + {y^4}\\ = - 2{x^5} + {y^4}\end{array}\) Đáp án A.
Câu 5 :
Có bao nhiêu số nguyên dương m thỏa mãn đa thức \(A = 4{x^2}{y^3} + 3{x^3}{y^2}\) chia hết cho đơn thức \(B = 2{x^2}{y^m}\)?
Đáp án : C Phương pháp giải :
Để đa thức chia hết cho đơn thức thì mọi hạng tử của đa thức phải chia hết cho đơn thức. Lời giải chi tiết :
Để \(A = 4{x^2}{y^3} + 3{x^3}{y^2}\) chia hết cho \(B = 2{x^2}{y^m}\) thì \(4{x^2}{y^3} \vdots 2{x^2}{y^m}\) và \(3{x^3}{y^2} \vdots 2{x^2}{y^m}\). Do đó \(3 \ge m\) và \(2 \ge m\). Kết hợp với điều kiện m là số nguyên dương thì \(0 < m \le 2\), hay m = 1; m = 2. Vậy có 2 giá trị nguyên dương của m. Đáp án C.
Câu 6 :
Biểu thức \(\left( {3x + y} \right)\left( {y - 3x} \right)\) bằng
Đáp án : B Phương pháp giải :
Sử dụng hằng đẳng thức hiệu hai bình phương \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\). Lời giải chi tiết :
Ta có: \(\left( {3x + y} \right)\left( {y - 3x} \right) = \left( {y + 3x} \right)\left( {y - 3x} \right) = {y^2} - 9{x^2}\). Đáp án B.
Câu 7 :
Điền vào chỗ trống: \(\left( {3x + y} \right)\left( {9{x^2} + ... + {y^2}} \right) = 27{x^3} + {y^3}\)
Đáp án : B Phương pháp giải :
Sử dụng hằng đẳng thức tổng hai lập phương \({a^3} + {b^3} = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\). Lời giải chi tiết :
Ta có: \(27{x^3} + {y^3} = \left( {3x + y} \right)\left( {9{x^2} - 3xy + {y^2}} \right)\) Ta điền \( - 3xy\) vào chỗ trống. Đáp án B.
Câu 8 :
Phân tích đa thức \({\left( {x - 4} \right)^2} + \left( {x - 4} \right)\) thành nhân tử, ta được:
Đáp án : B Phương pháp giải :
Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử. Lời giải chi tiết :
\({\left( {x - 4} \right)^2} + \left( {x - 4} \right) = \left( {x - 4} \right)\left( {x - 4 + 1} \right) = \left( {x - 4} \right)\left( {x - 3} \right)\). Đáp án B.
Câu 9 :
Cho tứ giác ABCD. Chọn khẳng định sai trong các khẳng định sau:
Đáp án : C Phương pháp giải :
Dựa vào định nghĩa tứ giác. Lời giải chi tiết :
Hai góc \(\widehat C\) và \(\widehat D\) là hai góc kề một đáy nên khẳng định C sai. Đáp án C.
Câu 10 :
Trong hình thang có hai góc tù thì
Đáp án : D Phương pháp giải :
Dựa vào định lí tổng các góc của hình thang. Lời giải chi tiết :
Xét hình thang ABCD có AB // CD nên \(\widehat A + \widehat D = 180^\circ \) (2 góc trong cùng phía) suy ra hai góc đó có nhiều nhất một góc nhọn, có nhiều nhất một góc tù. Tương tự \(\widehat B\) và \(\widehat C\) cũng vậy. Do đó trong bốn góc A, B, C, D có hai góc tù thì hai góc còn lại là hai góc nhọn. Đáp án D.
Câu 11 :
Cho hình thang cân ABCD có đáy nhỏ AB = 3cm, đường cao AH = 5cm và \(\widehat {BCD} = 45^\circ \). Độ dài đáy lớn CD là:
Đáp án : D Phương pháp giải :
Kẻ đường cao BK xuống CD. Chứng minh AH = DH = KC. Ta được độ dài đáy lớn. Lời giải chi tiết :
Kẻ đường cao BK xuống CD. Vì ABCD là hình thang cân nên AD = BC. Ta chứng minh được \(\Delta AHD = \Delta BKC\) (cạnh huyền – góc nhọn) nên DH = KC. Mà tam giác BKC vuông tại K có \(\widehat {BCK} = 45^\circ \) nên là tam giác vuông cân. Suy ra BK = KC = DH = 5cm. (1) Tứ giác ABKH là hình có AB // HK (gt), AH // BK (cùng vuông góc với CD) Suy ra ABKH là hình bình hành, suy ra AB = HK = 3cm. (2) Từ (1) và (2) suy ra DC = DH + HK + KC = 5 + 3 + 5 = 13 (cm) Đáp án D.
Câu 12 :
Phát biểu nào sau đây là đúng?
Đáp án : D Phương pháp giải :
Dựa vào dấu hiệu nhận biết của hình bình hành. Lời giải chi tiết :
Tứ giác có các cạnh đối song song là hình bình hành. Đáp án D.
II. Tự luận
Phương pháp giải :
a) Thu gọn đa thức để tìm bậc sau khi thu gọn. b) Sử dụng quy tắc trừ hai đa thức. c) Biến đổi để tính C, sử dụng quy tắc cộng hai đa thức. Lời giải chi tiết :
a) Ta có: \(\begin{array}{l}A = {x^4} - 2{x^2}y - {x^4} + {x^3} + {x^2}y - 1\\ = \left( {{x^4} - {x^4}} \right) + {x^3} + \left( { - 2{x^2}y + {x^2}y} \right) - 1\\ = {x^3} - {x^2}y - 1\end{array}\) Vậy đa thức A có bậc là 3. b) Ta có: \(\begin{array}{l}A - B = \left( {{x^2} + 2xy + {y^2}} \right) - \left( {{x^2} - 2xy + {y^2}} \right)\\ = {x^2} + 2xy + {y^2} - {x^2} + 2xy - {y^2}\\ = \left( {{x^2} - {x^2}} \right) + \left( {2xy + 2xy} \right) + \left( {{y^2} - {y^2}} \right)\\ = 4xy\end{array}\) c) Vì \(C - A = B\) nên \(C = A + B\) \(\begin{array}{l}C = \left( {{x^3} - 3{x^2}y + 3x{y^2} - {y^3}} \right) + \left( { - {x^3} + 3{x^2}y + {y^3} - 2} \right)\\ = {x^3} - 3{x^2}y + 3x{y^2} - {y^3} - {x^3} + 3{x^2}y + {y^3} - 2\\ = \left( {{x^3} - {x^3}} \right) + \left( { - {y^3} + {y^3}} \right) + \left( { - 3{x^2}y + 3{x^2}y} \right) + 3x{y^2} - 2\\ = 3x{y^2} - 2\end{array}\) Phương pháp giải :
a) Sử dụng hằng đẳng thức hiệu hai bình phương: \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) b) Dựa vào quy tắc chia đa thức cho đơn thức. Lời giải chi tiết :
a) \(\left( {x - 2y} \right)\left( {x + 2y} \right) = {x^2} - {\left( {2y} \right)^2} = {x^2} - 4{y^2}\) b) \(\left( {4{x^2}{y^2} + 3{x^3}{y^2} - {x^5}{y^4}} \right):\left( {{x^2}y} \right)\) \(\begin{array}{l} = 4{x^2}{y^2}:{x^2}y + 3{x^3}{y^2}:{x^2}y - {x^5}{y^4}:{x^2}y\\ = 4y + 3xy - {x^3}{y^3}\end{array}\) Phương pháp giải :
a) Sử dụng quy tắc nhân đa thức để rút gọn biểu thức A. b) Sử dụng hằng đẳng thức bình phương của một tổng: \({a^2} + 2ab + {b^2} = {\left( {a + b} \right)^2}\) để tính nhanh. Lời giải chi tiết :
a) Ta có: \(\begin{array}{l}A = \left( {x + y} \right)\left( {2x - y} \right) - 2x\left( {x + \frac{y}{2}} \right) + {y^2} + 2024\\ = 2{x^2} - xy + 2xy - {y^2} - 2{x^2} - xy + {y^2} + 2024\\ = \left( {2{x^2} - 2{x^2}} \right) - \left( {xy - 2xy + xy} \right) + \left( { - {y^2} + {y^2}} \right) + 2024\\ = 2024\end{array}\) Vậy giá trị của biểu thức không phụ thuộc vào giá trị của biến. c) Ta có: \({101^2} = {\left( {100 + 1} \right)^2} = {100^2} + 2.100.1 + {1^2} = 10\,000 + 200 + 1 = 10\,201.\) Phương pháp giải :
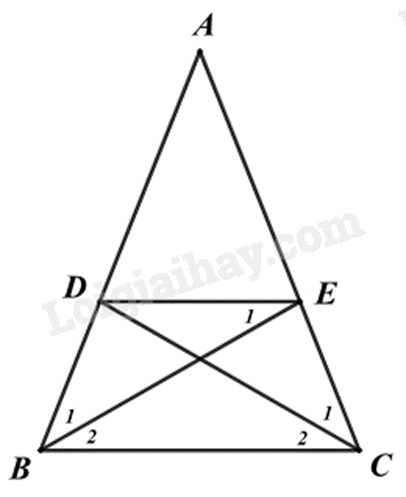
a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh góc cạnh. b) Chứng minh BDEC có một cặp cạnh đối song song nên là hình thang. Chứng minh hai cạnh bên BD = CE nên BDEC là hình thang cân. c) Dựa vào BD = DE và DE = EC suy ra tam giác BDE và tam giác DEC cân, suy ra \(\widehat {{B_1}} = \widehat {{B_2}}\) và \(\widehat {{C_1}} = \widehat {{C_2}}\). Lời giải chi tiết :
a) Xét tam giác ABE và ACD có: \(AB = AC\) (tam giác ABC cân tại A) \(\widehat A\) chung \(AE = AD\) (gt) Suy ra \(\Delta ABE = \Delta ACD\left( {c.g.c} \right)\) (đpcm) b) Vì AD = AE nên tam giác ADE cân tại A, suy ra \(\widehat {ADE} = \frac{{180^\circ - \widehat A}}{2}\) (tính chất tam giác cân) Tam giác ABC cân tại A, suy ra \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\) (tính chất tam giác cân) Suy ra \(\widehat {ADE} = \widehat {ABC}\). Mà hai góc này ở vị trí đồng vị nên DE // BC (cặp góc đồng vị bằng nhau) Do đó BDEC là hình thang. Ta có: AB = AC, AD = AE suy ra AB – AD = AC – AE hay BD = CE. Suy ra BDEC là hình thang cân (hình thang có hai cạnh bên bằng nhau). c) Theo đề bài, ta có BD = DE = EC. Tam giác BDE có BD = DE nên tam giác BDE cân tại D. Suy ra \(\widehat {{B_1}} = \widehat {{E_1}}\) Mà \(\widehat {{E_1}} = \widehat {{B_2}}\) (hai góc so le trong) Suy ra \(\widehat {{B_1}} = \widehat {{B_2}}\) hay BE là tia phân giác của \(\widehat {ABC}\). Tương tự, ta chứng minh được \(\widehat {{C_1}} = \widehat {{C_2}}\) hay CD là tia phân giác của \(\widehat {ACB}\). Vậy khi BE là tia phân giác của \(\widehat {ABC}\), CD là tia phân giác của \(\widehat {ACB}\) thì BD = DE = EC. Phương pháp giải :
a) Sử dụng hằng đẳng thức bình phương của một tổng: \({a^2} + 2ab + {b^2} = {\left( {a + b} \right)^2}\) và bình phương của một hiệu: \({a^2} - 2ab + {b^2} = {\left( {a - b} \right)^2}\) để biến đổi về dạng \({A^2} + {B^2} + c\). Khi đó giá trị nhỏ nhất là c (với c là hằng số). b) Gọi x, y (m) là các kích thước của hình chữ nhật. Biểu diễn diện tích theo x, y. Từ đó biểu diễn chu vi theo x, y để kiểm tra câu trả lời của bạn Nam. Lời giải chi tiết :
a) \({x^2} - 2xy + 2x + 2{y^2} - 4y + 2 = 0\) \(\begin{array}{l}{x^2} - 2xy + {y^2} + 2x - 2y + 1 + {y^2} - 2y + 1 = 0\\{\left( {x - y} \right)^2} + 2\left( {x - y} \right) + 1 + {\left( {y - 1} \right)^2} = 0\\{\left( {x - y + 1} \right)^2} + {\left( {y - 1} \right)^2} = 0\end{array}\) Vì \({\left( {x - y + 1} \right)^2} \ge 0\) và \({\left( {y - 1} \right)^2} \ge 0\) với mọi x, y nên \({\left( {x - y + 1} \right)^2} + {\left( {y - 1} \right)^2} = 0\) khi \(x - y + 1 = 0\) và \(y - 1 = 0\). +) \(y - 1 = 0\) suy ra \(y = 1\) +) \(x - y + 1 = 0\) hay \(x - 1 + 1 = 0\) suy ra \(x = 0\). Vậy \(x = 0\) và \(y = 1\). b) Gọi x, y (m) là các kích thước của hình chữ nhật. \(\left( {x;y > 0} \right)\) Vì hình chữ nhật có diện tích không đổi bằng \(100{m^2}\) nên ta có \(xy = 100\left( {{m^2}} \right)\). Ta có: \({\left( {x - y} \right)^2} \ge 0\) Suy ra \({x^2} - 2xy + {y^2} \ge 0\) \({x^2} + 2xy + {y^2} - 4xy \ge 0\) \({\left( {x + y} \right)^2} \ge 4xy = 4.100 = 400\) Suy ra \(x + y \ge \sqrt {400} = 20\). Do đó chu vi hình chữ nhật là \(C = 2\left( {x + y} \right) \ge 2.20 = 40\left( m \right)\) Dấu bằng xảy ra khi \(x = y = 10\) khi đó hình chữ nhật là hình vuông. Vậy bạn Nam trả lời đúng. Khi đó chu vi nhỏ nhất là 40m.
|