Đề thi giữa kì 2 Toán 8 Kết nối tri thức - Đề số 10Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.Đề bài
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Rút gọn biểu thức 5x2−10xy2(x−2y)3 được kết quả bằng
Câu 2 :
Phân thức đối của phân thức −2y5x3 là:
Câu 3 :
Mẫu thức chung của hai phân thức 32x3y4 và 45x4y3 là
Câu 4 :
Kết quả rút gọn của biểu thức x2+4x+49−(x+5)2 bằng
Câu 5 :
Kết quả của phép tính xy2xy+x2yxy bằng
Câu 6 :
Phân thức K(x) thỏa mãn K(x):x4−x=4−x2 là
Câu 8 :
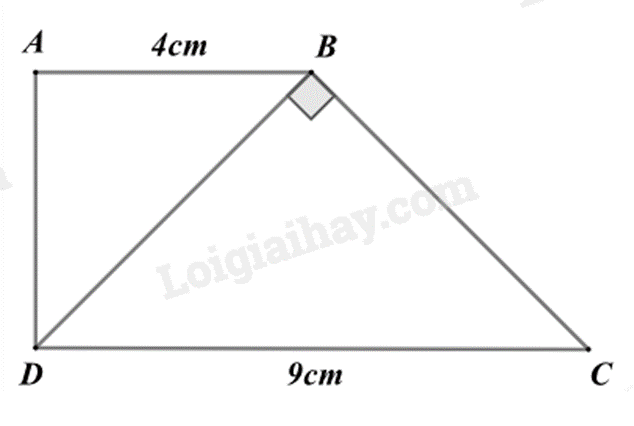
Cho hình thang vuông ABCD (ˆA=ˆD=90∘) có DB⊥BC, AB = 4cm, CD = 9cm. Độ dài đoạn thẳng BD là:
Câu 9 :
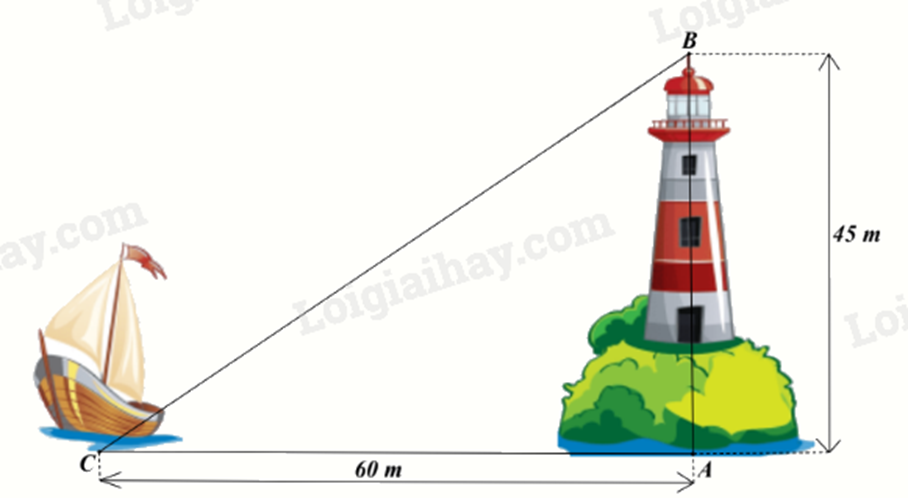
Ngọn hải đăng Lý Sơn (thuộc tỉnh Quảng Ngãi) cao 45m. Một con tàu đậu cách chân ngọn hải đăng 60m. Khoảng cách từ tàu đến đỉnh ngọn hải đăng là
Câu 10 :
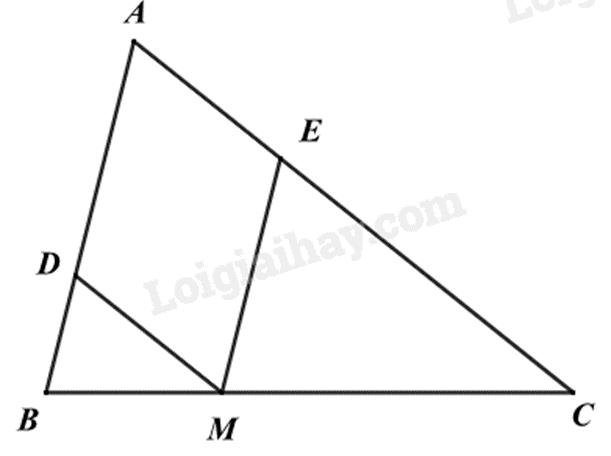
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho MBMC=12. Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Tỉ số chu vi hai tam giác ΔDBM và ΔEMC là
Câu 11 :
Cho ΔABC và ΔMNP có: ˆA=ˆM=90∘. Để kết luận ΔABC∽ΔMNP theo trường hợp cạnh huyền – cạnh góc vuông thì cần có thêm điều kiện nào sau đây
Phần II. Câu hỏi trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho biểu thức A=(x2+1x2+x+2x+1):(x+1)22x với x≠0;x≠−1. a) Rút gọn biểu thức A ta được kết quả A=−2x+1.
Đúng
Sai
b) Khi x=−1 thì giá trị biểu thức là 2.
Đúng
Sai
c) Biểu thức A=1 khi x=1.
Đúng
Sai
d) Để A∈Z thì x∈{−3;−2;1;0}.
Đúng
Sai
Câu 2 :
Cho ΔABC có AB = 2cm, AC = 4cm. Qua B dựng đường thẳng cắt AC tại D sao cho ^ABD=^ACB. Gọi AH là đường cao của ΔABC, AE là đường cao của ΔABD.
a) ΔABD∽ΔACB.
Đúng
Sai
b) ^ADB=^ABC.
Đúng
Sai
c) AD=0,5cm,DC=3,5cm.
Đúng
Sai
d) SΔABH=4SΔADE.
Đúng
Sai
Phần III. Câu hỏi trắc nghiệm trả lời ngắn
Thí sinh trả lời câu hỏi từ câu 1 đến câu 4
Câu 1 :
Cho phân thức H(x) thỏa mãn x3−x−H(x)=23−x. Giá trị của H(x) tại x=2 là. Đáp án:
Câu 2 :
Biết cái cây có chiều cao CD=5m và khoảng cách AC=32m, EC=8m. Chiều cao AB của ngôi nhà là …m.
Đáp án:
Câu 3 :
Một chiếc ti vi 24 inch có nghĩa là đường chéo màn hình của nó có độ dài là 24 inch (inch: đơn vị đo độ dài sử dụng ở nước Anh và một số nước khác, 1 inch ≈ 2,54cm). Biết một ti vi màn hình phẳng có chiều dài, chiều rộng của màn hình lần lượt là 14,8 inch và 11,8 inch thì tivi đó thuộc loại bao nhiêu inch? (làm tròn đến chữ số thập phân thứ nhất)
Đáp án:
Câu 4 :
Tổng các giá trị của y để biểu thức 1+y2+1y2+1y bằng 1 là Đáp án:
Phần IV. Tự luận
Lời giải và đáp án
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Rút gọn biểu thức 5x2−10xy2(x−2y)3 được kết quả bằng
Đáp án : A Phương pháp giải :
Chia cả tử và mẫu thức của biểu thức cho nhân tử chung. Lời giải chi tiết :
Ta có: 5x2−10xy2(x−2y)3=5x(x−2y)2(x−2y)3=5x2(x−2y)2 Đáp án A
Câu 2 :
Phân thức đối của phân thức −2y5x3 là:
Đáp án : B Phương pháp giải :
Phân thức đối của phân thức AB là −AB. Lời giải chi tiết :
Phân thức đối của phân thức −2y5x3 là −(−2y5x3)=2y5x3. Đáp án B
Câu 3 :
Mẫu thức chung của hai phân thức 32x3y4 và 45x4y3 là
Đáp án : A Phương pháp giải :
+ Phân tích mẫu thức của mỗi phân thức đã cho thành nhân tử + Mẫu thức chung cần tìm là một tích mà các nhân tử được chọn như sau: * Nhân tử bằng số của mẫu thức chung là tích các nhân tử bằng số của các mẫu dương ở Bước 1 (nếu các nhân tử bằng số của các mẫu thức là các số nguyên dương thì nhân tử bằng số của mẫu thức chung là BCNN của chúng); * Với mỗi lũy thừa của cùng một biểu thức có mặt trong các mẫu thức, ta chọn lũy thừa có số mũ cao nhất. Lời giải chi tiết :
Mẫu thức chung của hai phân thức 32x3y4 và 45x4y3 là: 10x4y4. Đáp án A
Câu 4 :
Kết quả rút gọn của biểu thức x2+4x+49−(x+5)2 bằng
Đáp án : B Phương pháp giải :
Phân tích tử thức, mẫu thức thành nhân tử sử dụng hằng đẳng thức sau đó chia cà tử và mẫu cho nhân tử chung. Lời giải chi tiết :
Ta có: x2+4x+49−(x+5)2=(x+2)2(3−x−5)(3+x+5)=(x+2)2(−x−2)(x+8)=(x+2)2−(x+2)(x+8)=−x−2x+8 Đáp án B
Câu 5 :
Kết quả của phép tính xy2xy+x2yxy bằng
Đáp án : D Phương pháp giải :
Sử dụng quy tắc cộng hai phân thức cùng mẫu: AB+CB=A+CB. Lời giải chi tiết :
Ta có: xy2xy+x2yxy=xy2+x2yxy=xy(y+x)xy=x+y. Đáp án D
Câu 6 :
Phân thức K(x) thỏa mãn K(x):x4−x=4−x2 là
Đáp án : C Phương pháp giải :
Chuyển vế để tìm K(x). Lời giải chi tiết :
Ta có: K(x):x4−x=4−x2K(x)=4−x2.x4−xK(x)=(4−x).x2(4−x)K(x)=x2 Đáp án C
Đáp án : D Phương pháp giải :
Dựa vào hai tam giác đồng dạng suy ra tỉ lệ giữa các cạnh tương ứng của hai tam giác đó. Lời giải chi tiết :
ΔGHI∽ΔFEI nên HIIE=GHEF Thay số: xy=510=12. Đáp án D
Câu 8 :
Cho hình thang vuông ABCD (ˆA=ˆD=90∘) có DB⊥BC, AB = 4cm, CD = 9cm. Độ dài đoạn thẳng BD là:
Đáp án : A Phương pháp giải :
Chứng minh ΔABD∽ΔBDC suy ra tỉ lệ giữa các cặp cạnh tương ứng, biến đổi để tính BD. Lời giải chi tiết :
Xét ΔABD và ΔBDC có: ^BAD=^DBC(=90∘) ^ABD=^BDC (hai góc so le trong) nên ΔABD∽ΔBDC (g.g) suy ra ABBD=BDCD, do đó BD2=AB.CD=4.9=36 suy ra BD=√36=6(cm). Đáp án A
Câu 9 :
Ngọn hải đăng Lý Sơn (thuộc tỉnh Quảng Ngãi) cao 45m. Một con tàu đậu cách chân ngọn hải đăng 60m. Khoảng cách từ tàu đến đỉnh ngọn hải đăng là
Đáp án : A Phương pháp giải :
Sử dụng định lí Pythagore vào tam giác ABC vuông tại A. Lời giải chi tiết :
Khoảng cách từ tàu đến đỉnh ngọn hải đăng là độ dài đoạn BC trong hình vẽ. Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có: BC2=AB2+AC2=452+602 Suy ra BC=√452+602=75(m) Đáp án A
Câu 10 :
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho MBMC=12. Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Tỉ số chu vi hai tam giác ΔDBM và ΔEMC là
Đáp án : B Phương pháp giải :
Sử dụng định lí hai tam giác đồng dạng để chứng minh ΔBDM∽ΔBAC,ΔCEM∽ΔCAB, suy ra ΔBDM∽ΔMEC. Tỉ số chu vi của hai tam giác đồng dạng bằng tỉ số các cạnh tương ứng của hai tam giác đồng dạng đó. Lời giải chi tiết :
Vì DM // AC nên ΔBDM∽ΔBAC (định lí hai tam giác đồng dạng) Vì ME // AC nên ΔCEM∽ΔCAB (định lí hai tam giác đồng dạng) Suy ra ΔBDM∽ΔMEC. Do đó BDME=BMMC=DMEC=12. Do đó CΔBDMCΔMEC=12. Đáp án B
Câu 11 :
Cho ΔABC và ΔMNP có: ˆA=ˆM=90∘. Để kết luận ΔABC∽ΔMNP theo trường hợp cạnh huyền – cạnh góc vuông thì cần có thêm điều kiện nào sau đây
Đáp án : B Phương pháp giải :
Trường hợp cạnh huyền – cạnh góc vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng. Lời giải chi tiết :
Để ΔABC∽ΔMNP(ˆA=ˆM=90∘) theo trường hợp cạnh huyền – cạnh góc vuông thì ta cần thêm điều kiện ABMN=BCNP hoặc ACMP=BCNP. Vậy đáp án B đúng. Đáp án B
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về hai hình đồng dạng: + Hai hình H, H’ được gọi là đồng dạng nếu có hình H1 đồng dạng phối cảnh với hình H và bằng hình H’. + Hình H đồng dạng với hình H’ nếu hình H’ bằng H hoặc bằng một hình phóng to hoặc thu nhỏ của H. Lời giải chi tiết :
Cặp hình trong hình 1 là hai hình đồng dạng. Đáp án A
Phần II. Câu hỏi trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Cho biểu thức A=(x2+1x2+x+2x+1):(x+1)22x với x≠0;x≠−1. a) Rút gọn biểu thức A ta được kết quả A=−2x+1.
Đúng
Sai
b) Khi x=−1 thì giá trị biểu thức là 2.
Đúng
Sai
c) Biểu thức A=1 khi x=1.
Đúng
Sai
d) Để A∈Z thì x∈{−3;−2;1;0}.
Đúng
Sai
Đáp án
a) Rút gọn biểu thức A ta được kết quả A=−2x+1.
Đúng
Sai
b) Khi x=−1 thì giá trị biểu thức là 2.
Đúng
Sai
c) Biểu thức A=1 khi x=1.
Đúng
Sai
d) Để A∈Z thì x∈{−3;−2;1;0}.
Đúng
Sai
Phương pháp giải :
a) Sử dụng các quy tắc tính toán với phân thức. b) Kiểm tra xem x=−1 có thoả mãn điều kiện không, nếu có, thay x=−1 vào A. c) Từ A=1 giải để tìm x. d) Để A nguyên thì kg(x) nguyên, hay k⋮g(x). Lập bảng để tìm các giá trị của x. Lời giải chi tiết :
a) Sai Ta có: A=(x2+1x2+x+2x+1):(x+1)22x với x≠0;x≠−1 =[x2+1x(x+1)+2xx(x+1)].2x(x+1)2=x2+2x+1x(x+1).2x(x+1)2=(x+1)2.2xx(x+1)3=2x+1 b) Sai Vì x=−1 không thoả mãn điều kiện xác định nên ta không tính được giá trị của A. c) Đúng Ta có: A=12x+1=1x+1=2x=2−1x=1 Vậy x=1 thì A=1. d) Sai Để A∈Z thì 2x+1 nguyên, hay (x+1)∈ Ư(2)={−2;−1;1;2}. Ta có bảng giá trị sau: Vậy x={−3;−2;1} thì A có giá trị nguyên. Đáp án: SSĐS
Câu 2 :
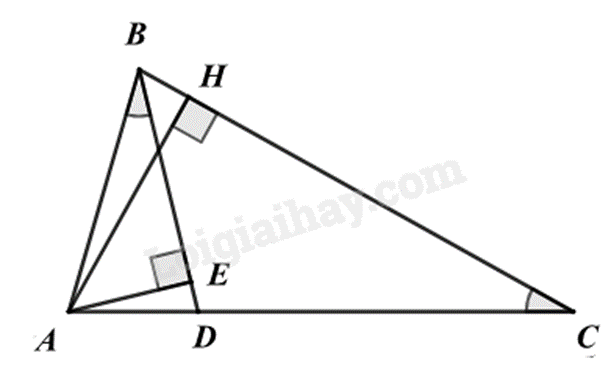
Cho ΔABC có AB = 2cm, AC = 4cm. Qua B dựng đường thẳng cắt AC tại D sao cho ^ABD=^ACB. Gọi AH là đường cao của ΔABC, AE là đường cao của ΔABD.
a) ΔABD∽ΔACB.
Đúng
Sai
b) ^ADB=^ABC.
Đúng
Sai
c) AD=0,5cm,DC=3,5cm.
Đúng
Sai
d) SΔABH=4SΔADE.
Đúng
Sai
Đáp án
a) ΔABD∽ΔACB.
Đúng
Sai
b) ^ADB=^ABC.
Đúng
Sai
c) AD=0,5cm,DC=3,5cm.
Đúng
Sai
d) SΔABH=4SΔADE.
Đúng
Sai
Phương pháp giải :
a) Sử dụng trường hợp đồng dạng góc – góc. b) Từ hai tam giác đồng dạng suy ra các góc tương ứng bằng nhau. c) Từ hai tam giác đồng dạng tỉ lệ giữa các cạnh tương ứng. d) Chứng minh ΔABH∽ΔADE suy ra tỉ số đồng dạng k của hai tam giác. Tỉ số đồng dạng của diện tích hai tam giác bằng k2. Lời giải chi tiết :
a) Đúng Xét ΔABD và ΔACB có: ^ABD=^ACB (chung) ˆA chung suy ra ΔABD∽ΔACB (g.g) b) Đúng Vì ΔABD∽ΔACB (ý a) nên ^ADB=^ABC (2 góc tương ứng) c) Sai Vì ΔABD∽ΔACB nên ABAC=ADAB Thay số 24=AD2, suy ra AD=2.24=1(cm). Do đó DC=AC−AD=4−1=3(cm). d) Đúng Ta có: ^ADB=^ABC (ý b), hay ^ADE=^ABH. Xét ΔABH và ΔADE có: ^AHB=^AED(=90∘) ^ADE=^ABH (cmt) suy ra ΔABH∽ΔADE (g.g) Suy ra AEAH=DEBH=ABAD=21=2=k. Do đó SΔABHSΔADE=k2=22=4. Suy ra SΔABH=4SΔADE. Đáp án: ĐĐSĐ
Phần III. Câu hỏi trắc nghiệm trả lời ngắn
Thí sinh trả lời câu hỏi từ câu 1 đến câu 4
Câu 1 :
Cho phân thức H(x) thỏa mãn x3−x−H(x)=23−x. Giá trị của H(x) tại x=2 là. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng quy tắc chuyển vế và trừ hai phân thức cùng mẫu để tính H(x). Sau đó thay x=2 (kiểm tra điều kiện của H(x)) vào phân thức H(x). Lời giải chi tiết :
Ta có: x3−x−H(x)=23−xH(x)=x3−x−23−xH(x)=x−23−x ĐKXĐ của H(x) là x≠3. Thay x=2 (TM) vào H(x), ta được: H(2)=2−23−2=0. Đáp án: 0
Câu 2 :
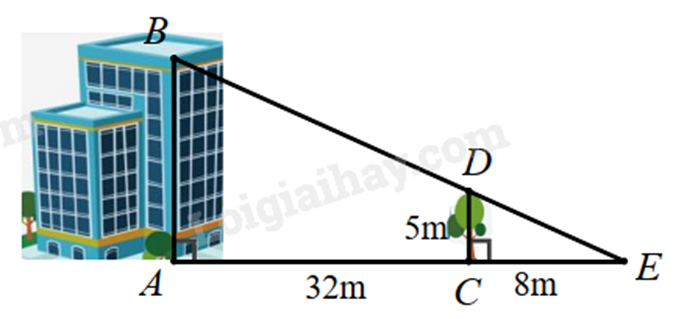
Biết cái cây có chiều cao CD=5m và khoảng cách AC=32m, EC=8m. Chiều cao AB của ngôi nhà là …m.
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Từ đề bài xác định được độ dài các đoạn thẳng tương ứng. Sử dụng định lí hai tam giác đồng dạng để chứng minh ΔCDE∽ΔABE. Từ đó biểu diễn tỉ lệ giữa các cạnh tương ứng để tính AB. Lời giải chi tiết :
Vì cái cây và ngôi nhà cùng vuông góc với mặt đất nên chúng song song với nhau nên CD // AB. Do đó ΔCDE∽ΔABE (định lí hai tam giác bằng nhau) Suy ra CEAE=CDAB hay CEAC+CE=CDAB Thay số: 832+8=5AB, suy ra AB=5:832+8=25(m) Vậy chiều cao AB của ngôi nhà là 25m. Đáp án: 25
Câu 3 :
Một chiếc ti vi 24 inch có nghĩa là đường chéo màn hình của nó có độ dài là 24 inch (inch: đơn vị đo độ dài sử dụng ở nước Anh và một số nước khác, 1 inch ≈ 2,54cm). Biết một ti vi màn hình phẳng có chiều dài, chiều rộng của màn hình lần lượt là 14,8 inch và 11,8 inch thì tivi đó thuộc loại bao nhiêu inch? (làm tròn đến chữ số thập phân thứ nhất)
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Áp dụng định lí Pythagore vào tam giác vuông để tính được đường chéo của tam giác vuông. Lời giải chi tiết :
Giả sử ta có tam giác ABC với chiều rộng AB = 11,8 inch, chiều dài AC = 14,8 inch. Khi đó đường chéo của tam giác ABC là: BC=√AB2+AC2=√11,82+14,82≈19(inch) Vậy tivi đó thuộc loại 19 inch. Đáp án: 19
Câu 4 :
Tổng các giá trị của y để biểu thức 1+y2+1y2+1y bằng 1 là Đáp án: Đáp án
Đáp án: Phương pháp giải :
Viết biểu thức bằng 1 rồi giải để tìm các giá trị y thoả mãn. Lời giải chi tiết :
1+y2+1y2+1y (ĐKXĐ:y≠0, y≠−12) Ta có: 1+y2+1y2+1y=1 1+y2+1y=2+1y1+y2+1y−2−1y=0y2−1=0y2=1y=±1 Vậy tổng các giá trị của y để biểu thức 1+y2+1y2+1y bằng 1 là: −1+1=0 Đáp án: 0
Phần IV. Tự luận
Phương pháp giải :
a) Sử dụng quy tắc cộng hai phân thức khác mẫu: - Quy đồng mẫu thức - Cộng các tử thức với nhau và giữ nguyên mẫu thức - Rút gọn phân thức (nếu cần). b) Rút gọn biểu thức ở vế trái, khi đó ta sẽ tìm được đa thức A. Lời giải chi tiết :
a) Ta có: 12(x+3)+32x(x+3)=x2x(x+3)+32x(x+3)=x+32x(x+3)=12x b) Ta có: Ax−2=2x3+4x2x2−4 Ax−2=2x2(x+2)(x+2)(x−2)Ax−2=2x2x−2 suy ra A=2x2. Phương pháp giải :
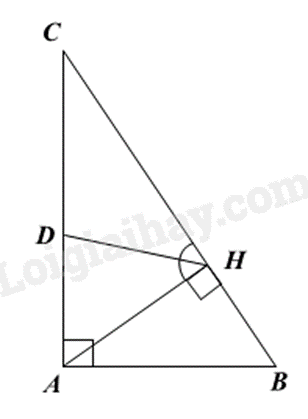
a) Chứng minh ΔABC∽ΔHBA theo trường hợp góc – góc. b) Chứng minh ΔAHC∽ΔBHA(g.g), suy ra tỉ lệ giữa các cạnh tương ứng, từ đó ta có: AH2=HB.HC Nhân cả hai vế với HC và biểu diễn tỉ lệ thức tạo thành: HBHC=AH2HC2. Sử dụng tính chất của đường phân giác trong tam giác, ta có: AHHC=ADDC (HD là đường phân giác của tam giác AHC) Kết hợp ta được điều phải chứng minh. Lời giải chi tiết :
a) Xét ΔABC và ΔHBA, ta có: ˆA=ˆH(=90∘)ˆBchung Suy ra ΔABC∽ΔHBA(g.g). c) Xét ΔAHC và ΔBHA có: ^AHC=^BHA(=90∘) ^CAH=^ABH (cùng phụ với ˆC) Suy ra ΔAHC∽ΔBHA(g.g) Do đó AHHC=HBAH suy ra AH2=HB.HC Nhân cả hai vế với HC, ta được: AH2.HC=HB.HC2 Do đó HBHC=AH2HC2 Mà HD là đường phân giác của tam giác AHC nên AHHC=ADDC Do đó HBHC=AD2DC2 (đpcm). Phương pháp giải :
Sử dụng định lí tổng 3 góc trong một tam giác bằng 180∘ suy ra ˆB=90∘. Chứng minh ΔABC∽ΔADB(g.g), suy ra tỉ lệ đồng dạng giữa các cạnh tương ứng, từ đó tính AB. Lời giải chi tiết :
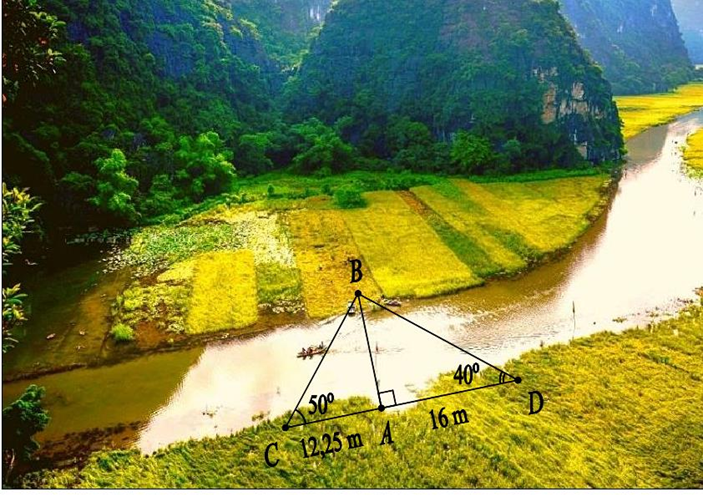
Xét tam giác ABC có ˆB=180∘−(ˆC+ˆD)=180∘−(50∘+40∘)=90∘ Xét ΔABC và ΔADB có: ^CAB=^BAD(=90∘) ˆC=^ABD (cùng phụ với ˆD) nên ΔABC∽ΔADB(g.g) suy ra ABAD=ACAB Do đó AB2=AD.AC Suy ra AB=√AD.AC=√16.12,25=14 Vậy khoảng cách AB là 14m.
|