Đề thi giữa kì 1 Toán 8 - Đề số 5 - Kết nối tri thứcTải về Câu 1: Kết quả của phép nhân đa thức (4{{rm{x}}^5} + 7{{rm{x}}^2}) với đơn thức ( - 3{{rm{x}}^3}) là : Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên
Lựa chọn câu để xem lời giải nhanh hơn
Đề bài Phần trắc nghiệm (2 điểm) Câu 1: Kết quả của phép nhân đa thức 4x5+7x2 với đơn thức −3x3 là : A. 12x8+21x5. B. −12x8+21x5. C. 12x8−21x5. D. −12x8−21x5. Câu 2: Khi viết đa thức 9x2+1−6x dưới dạng lũy thừa, ta được kết quả là A. (x−3)2. B. (x+3)(x−3). C. (1−3x)2. D. (3x+1)2. Câu 3: Để biểu thức x3−3x2+3x+a trở thành lập phương một hiệu thì a được thay bằng A. 3. B. 1. C. 9. D. -1. Câu 4: Giá trị của biểu thức 12x2y2:(−9xy2) tại là A. 4. B. -4. C. 12. D. -12. Câu 5: Kết quả của phép tính 15.91,5+150.0,85 là A. 120. B. 150. C. 1200. D. 1500. Câu 6: Thu gọn biểu thức (a−b)3+(a+b)3−6ab2 ta được kết quả là A. 2a3. B. 2a3+2b3. C. 2a2−6a2b. D. 2a3+6ab2. Câu 7: Hình thang là hình thang cân nếu ? A. Hai cạnh bên bằng nhau B. Hai đường chéo bằng nhau C. Hai góc đối bằng nhau D. Hai cạnh đối bằng nhau Câu 8: Khẳng định nào sau đây đúng A. Hình bình hành có một góc vuông là hình thoi. B. Tứ giác có hai cặp cạnh đối song song là hình bình hành. C. Hình thang có một góc vuông là hình chữ nhật. D. Hình thoi có một góc 60o thì trở thành hình chữ nhật. Câu 9: Hình bình hành ABCD có số đo góc A bằng 2 lần số đo góc B. Khi đó số đo góc D là: A. 600. B. 1200. C. 3000. D. 450. Câu 10: Hình bình hành MNPQ là hình chữ nhật nếu có A. MN = PQ. B. MP = NQ. C. NP = MQ. D. MN = MQ.
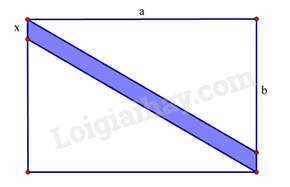
Phần tự luận (8 điểm) Bài 1. (3 điểm) 1. Thực hiện phép tính : (x3y3 – x2y3 – 4x3y2) : 2x2y2. 2. Cho biểu thức : A = (x – 2)3 – x2(x – 4) - 12x + 8 B = (x2 – 6x + 9) : (x – 3) – x(x + 7) – 9 a) Thu gọn biểu thức A và B. b) Tính giá trị của biểu thức A tại giá trị x = - 1. c) Biết C = A + B. Chứng minh C luôn âm với mọi giá trị của x. Bài 2. (2 điểm) 1) Tìm x, biết (2x+2)2−(2x−1)2=0 2) Biết số tự nhiên a chia cho 5 dư 4. Chứng minh rằng a2 chia cho 5 dư 1. 3) Tìm giá trị nhỏ nhất của biểu thức Q=5x2+5y2+8xy−2x+2y+2. Bài 3. (0,5 điểm) Viết đa thức biểu thị phần màu xanh trong hình sau:
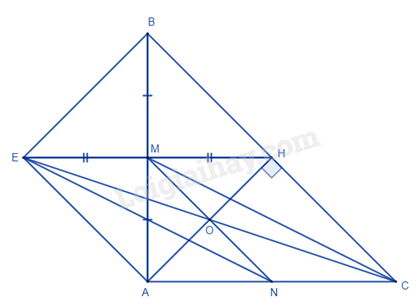
Bài 4. (2,5 điểm) Cho tam giác ABC vuông cân tại A, đường cao AH. Gọi M là trung điểm của AB,E đối xứng với H qua M. 1. Tứ giác AHBE là hình gì? Vì sao? 2. Chứng minh AEHC là hình bình hành. 3. Gọi O là giao điểm của AHvà EC,N là trung điểm của AC. Chứng minh M,O,N thẳng hàng. ---- Hết ---- Lời giải Phần trắc nghiệm (2 điểm)
Câu 1: Kết quả của phép nhân đa thức 4x5+7x2 với đơn thức −3x3 là :
Phương pháp Sử dụng quy tắc nhân đa thức với đơn thức: ta nhân từng hạng tử của đa thức với đơn thức sau đó cộng các kết quả với nhau. Lời giải Ta có: (4x5+7x2)(−3x3)=4x5.(−3x3)+(7x2)(−3x3)=−12x8−21x5 Đáp án D. Câu 2: Khi viết đa thức 9x2+1−6x dưới dạng lũy thừa, ta được kết quả là
Phương pháp Lựa chọn phương pháp phân tích đa thức thành nhân tử phù hợp. Lời giải 9x2+1−6x=(3x)2−2.3x+1=(3x−1)2. Đáp án D. Câu 3: Để biểu thức x3−3x2+3x+a trở thành lập phương một hiệu thì a được thay bằng
Phương pháp Sử dụng hằng đẳng thức lập phương của một hiệu để tìm a. Lời giải x3−3x2+3x+a=x3−3.x2.1+3.x.(−1)2+a. Để biểu thức trở thành lập phương của một hiệu thì a=(−1)3=−1. Vậy a = -1. Đáp án D. Câu 4: Giá trị của biểu thức 12x2y2:(−9xy2) tại là
Phương pháp Dựa vào quy tắc chia đơn thức cho đơn thức. Lời giải Ta có: 12x2y2:(−9xy2)=[12:−9].(x2:x).(y2:y2)=−43x Thay x=−3 và y=1,005 vào biểu thức ta được: −43.(−3)=4. Đáp án A. Câu 5: Kết quả của phép tính 15.91,5+150.0,85 là
Phương pháp Tìm nhân tử chung để thực hiện phép tính nhanh. Lời giải Ta có: 15.91,5+150.0,85=15.91,5+15.8,5=15(91,5+8,5)=15.100=1500 Đáp án D. Câu 6: Thu gọn biểu thức (a−b)3+(a+b)3−6ab2 ta được kết quả là
Phương pháp Sử dụng các hằng thức đáng nhớ để rút gọn. Lời giải Ta có: (a−b)3+(a+b)3−6ab2=(a−b+a+b)[(a−b)2−(a−b)(a+b)+(a+b)2]−6ab2=2a(a2−2ab+b2−a2+b2+a2+2ab+b2)−6ab2=2a(a2+3b2)−6ab2=2a3+6ab2−6ab2=2a3 Đáp án A. Câu 7: Hình thang là hình thang cân nếu ?
Phương pháp Dựa vào dấu hiệu nhận biết một hình thang cân. Lời giải Hình thang có hai đường chéo bằng nhau là hình thang cân. Đáp án B. Câu 8: Khẳng định nào sau đây đúng A. Hình bình hành có một góc vuông là hình thoi. B. Tứ giác có hai cặp cạnh đối song song là hình bình hành. C. Hình thang có một góc vuông là hình chữ nhật. D. Hình thoi có một góc 60o thì trở thành hình chữ nhật. Phương pháp Dựa vào dấu hiệu nhận biết của các hình đã học. Lời giải Trong các khẳng định trên, chỉ có khẳng định B là đúng. Đáp án B. Câu 9: Hình bình hành ABCD có số đo góc A bằng 2 lần số đo góc B. Khi đó số đo góc D là:
Phương pháp Trong hình bình hành, hai góc kề nhau thì bù nhau, hai góc đối nhau thì bằng nhau. Lời giải Ta có góc A và góc B là hai góc kề một cạnh nên ˆA+ˆB=1800. Mà góc A bằng 2 lần góc B nên ta có: 2ˆB+ˆB=18003ˆB=1800ˆB=1800:3=600 Đáp án A. Câu 10: Hình bình hành MNPQ là hình chữ nhật nếu có A. MN = PQ. B. MP = NQ. C. NP = MQ. D. MN = MQ. Phương pháp Dựa vào dấu hiệu nhận biết hình chữ nhật. Lời giải Hình bình hành MNPQ là hình chữ nhật nếu hai đường chéo của hình bình hành MNPQ bằng nhau, hay MP = NQ. Đáp án B.
Phần tự luận. (8 điểm) Bài 1. (3 điểm) 1. Thực hiện phép tính : (x3y3 – x2y3 – 4x3y2) : 2x2y2. 2. Cho biểu thức : A = (x – 2)3 – x2(x – 4) - 12x + 8 B = (x2 – 6x + 9) : (x – 3) – x(x + 7) – 9 a) Thu gọn biểu thức A và B. b) Tính giá trị của biểu thức A tại giá trị x = - 1. c) Biết C = A + B. Chứng minh C luôn âm với mọi giá trị của x. Phương pháp 1. Áp dụng quy tắc chia đa thức cho đơn thức. 2. a) Thu gọn biểu thức A và B bằng cách sử dụng các quy tắc tính toán với đa thức. b) Thay x = -1 vào biểu thức A để tính giá trị của A. c) Sử dụng quy tắc cộng để tìm C. Biến đổi C thành tích của một số âm và số dương nên luôn âm với mọi x. Lời giải 1. Ta có (x3y3−x2y3−4x3y2):2x2y2=x3y3:2x2y2−x2y3:2x2y2−4x3y2:2x2y2=12xy−12y−2x 2. a) Ta có: A=(x−2)3−x2(x−4)−12x+8=x3−6x2+12x−8−x3+4x2−12x+8=−2x2 B=(x2−6x+9):(x−3)−x(x+7)−9=(x−3)2:(x−3)−x2−7x−9=x−3−x2−7x−9=−x2−6x−12 b) Thay x = -1 vào A, ta được: A = -2.(-1)2 = -2. c) Ta có: C=A+B=−2x2+(−x2−6x−12)=−2x2−x2−6x−12=−3x2−6x−12=−3(x2+2x+4)=−3.[(x2+2x+1)+3]=−3[(x+1)2+3] Vì (x+1)2≥0∀x∈R ⇒(x+1)2+3≥3∀x∈R⇒−3.[(x+1)2+3]≤−3.3=−9∀x∈R Vậy C luôn âm với mọi giá trị x. Bài 2. (2 điểm) 1) Tìm x, biết (2x+2)2−(2x−1)2=0 2) Biết số tự nhiên a chia cho 5 dư 4. Chứng minh rằng a2 chia cho 5 dư 1. 3) Tìm giá trị nhỏ nhất của biểu thức Q=5x2+5y2+8xy−2x+2y+2. Phương pháp 1) Sử dụng các phương pháp phân tích đa thức để tìm x. 2) Đặt a = 5k + 4. Sử dụng hằng đẳng thức để tách a2 thành tổng của các hạng tử, chứng minh a2 chia 5 dư 1. 3) Biến đổi biểu thức thành tổng của các đa thức bậc 2 + hằng số. Lời giải 1) Ta có: (2x+2)2−(2x−1)2=0 (2x+2−2x+1)(2x+2+2x−1)=03(4x+1)=04x+1=04x=−1x=−14 Vậy x=−14. 2) Vì a chia cho 5 dư 4 nên gọi a = 5k + 4 (k∈Z). Khi đó ta có: a2=(5k+4)2a2=25k2+40k+16 Vì 25⋮5⇒25k2⋮5;40⋮5⇒40k⋮5 nên (25k2+40k)⋮5 Vì 16 chia cho 5 dư 1 nên 25k2+40k+16 chia cho 5 dư 1 hay a2 chia cho 5 dư 1. 3) Ta có: Q=5x2+5y2+8xy−2x+2y+2=4x2+x2+4y2+y2+8xy−2x+2y+1+1=(4x2+8xy+4y2)+(x2−2x+1)+(y2+2y+1)=(2x+2y)2+(x−1)2+(y+1)2 Vì (2x+2y)2≥0,∀x,y∈R;(x−1)2≥0,∀x∈R;(y+1)2≥0,∀y∈R. nên (2x+2y)2+(x−1)2+(y+1)2≥0,∀x,y∈R. Dấu “=” xảy ra khi và chỉ khi {2x+2y=0x−1=0y+1=0⇔{x=1y=−1. Vậy giá trị nhỏ nhất của biểu thức Q là 0 khi và chỉ khi x = 1 và y = -1. Bài 3. (0,5 điểm) Viết đa thức biểu thị phần màu xanh trong hình sau:
Phương pháp - Viết đa thức biểu thị diện tích hình chữ nhật, hai hình tam giác vuông. - Diện tích phần màu xanh bằng diện tích hình chữ nhật trừ đi diện tích hai hình tam giác vuông. Lời giải Hình chữ nhật lớn có chiều dài là a, chiều rộng là (b + x). => Diện tích hình chữ nhật là: Shcn = a(b + x) = ab + ax. Ta thấy hai hình tam giác trên bằng nhau có độ dài hai cạnh là a và b => Diện tích hình tam giác là: Stam giác = ab2. Đa thức biểu thị diện tích phần màu xanh trong hình là: Sphần màu xanh = Shcn – 2.Stam giác = ab + ax – 2.ab2 = ab + ax – ab = ax. Bài 4. (2,5 điểm) Cho tam giác ABC vuông cân tại A, đường cao AH. Gọi M là trung điểm của AB,E đối xứng với H qua M. 1. Tứ giác AHBE là hình gì? Vì sao? 2. Chứng minh AEHC là hình bình hành. 3. Gọi O là giao điểm của AHvà EC,N là trung điểm của AC. Chứng minh M,O,N thẳng hàng. Phương pháp 1. Sử dụng tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông ABC, dấu hiệu nhận biết các hình đã học để chứng minh AHBE là hình vuông. 2. Chứng minh tứ giác AEHC có cặp cạnh đối song song và bằng nhau nên là hình bình hành. 3. Chứng minh O là giao điểm của hai đường chéo trong hình bình hành EMCN nên O nằm giữa M và N hay M, O, N thẳng hàng. Lời giải 1. Xét tam giác ABC vuông cân tại A, ta có AH là đường cao nên AH cũng là đường trung tuyến ứng với cạnh huyền của tam giác ABC => AH = 12BC = BH = HC. Xét tứ giác AHBE có: AM = MB (M là trung điểm của AB). EM = MH (E đối xứng với H qua M). => AHBE là hình bình hành (hai đường chéo cắt nhau tại trung điểm). Xét hình bình hành AHBE có ^AHB=900 => AHBE là hình chữ nhật (hình bình hành có một góc vuông). Xét hình chữ nhật AHBE có AH = BH (cmt) => AHBE là hình vuông (hình chữ nhật có hai cạnh kề bằng nhau). => AE // BH, AE = BH. 2. Xét tứ giác AEHC có: AE // HC (vì AE // BH) AE = HC (= HB) => AEHC là hình bình hành (cặp cạnh đối song song và bằng nhau). (đpcm) 3. Vì O là giao điểm của AH và EC nên O là trung điểm của EC => EO = OC. Vì AEHC là hình bình hành nên EH // AC và EH = AC. Ta có M là trung điểm của EH, N là trung điểm của AC nên EM = MH = 12EB = 12AC = AN = NC. Xét tứ giác EMCN có: EM // CN (vì EH // AC) EM = CN (cmt) => EMCN là hình bình hành (cặp cạnh đối song song và bằng nhau) => EC cắt MN tại trung điểm của mỗi đường. Mà O là trung điểm của EC nên O cũng là trung điểm của MN, hay M, O, N thẳng hàng (đpcm).
|