Đề kiểm tra học kì 1 Toán 9 - Đề số 30Tải về Đáp án và lời giải chi tiết Đề số 30 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9
Lựa chọn câu để xem lời giải nhanh hơn
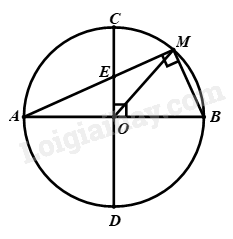
Đề bài Câu 1: (2,5 điểm) Cho biểu thức \(A = \frac{{x - 4}}{{\sqrt x + 1}}\) và \(B = \frac{{\sqrt x + 1}}{{\sqrt x - 2}} + \frac{{\sqrt x + 2}}{{1 - \sqrt x }} + \frac{{\sqrt x - 4}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x - 2} \right)}}\) a) Tính giá trị của biểu thức \(A\) khi \(x = 16\). b) Rút gọn biểu thức \(B\). c) Tìm \(x\) để biểu thức \(M = A.B\) nhận giá trị nguyên. Câu 2: (2 điểm) Cho hàm số \(y = \left( {1 - m} \right)x + m + 2\) (với \(m\) là tham số) có đồ thị là đường thẳng \(d\). Xác định \(m\) để: a) Đường thẳng \(d\) cắt trục hoành tại điểm có hoành độ bằng 2. b) Đường thẳng \(d\) song song với đường thẳng \(y = 2x - 1\) c) Đường thẳng \(d\) cắt trục \(Ox,Oy\) lần lượt tại hai điểm \(A,B\) sao cho tam giác \(AOB\) vuông cân. Câu 3: (1,5 điểm) 1) Giải hệ phương trình: \(\left\{ \begin{array}{l}2\left| {x - 1} \right| - \frac{3}{{\sqrt {y + 3} }} = - 3\\\left| {x - 1} \right| + \frac{1}{{\sqrt {y + 3} }} = 1\end{array} \right.\) 2) Giá niêm yết của các chiếc tủ lạnh cùng loại trong siêu thị là như nhau. Gian hàng A bán với giá khuyên mãi \(20\% \). Gian hàng B, lần 1 giảm giá \(10\% \) cũng bán được chưa được nên giảm tiếp \(10\% \) nữa so với giá đã giảm lần thứ nhất. Nếu là người mua hàng, để mua được giá rẻ hơn em sẽ chọn mua ở gian hàng nào? Vì sao? Câu 4: (3,5 điểm) Cho đường tròn \(\left( {O;R} \right)\) có hai đường kính \(AB\) và \(CD\) vuông góc với nhau. Điểm \(E\) thay đổi thuộc đoạn \(OC,\) nối \(AE\) cắt đường tròn \(\left( O \right)\) tại \(M\). a) Chứng minh 4 điểm \(O,B,M,E\) cùng nằm trên một đường tròn. b) Chứng minh \(AE.AM\) không phụ thuộc vào vị trí của điểm \(E\) trên đoạn \(OC\). c) Xác định vị trí của \(E\) trên đoạn \(OC\) để \(MA = 2MB\). d) Xác định vị trí của điểm \(E\) trên đoạn \(OC\) để chu vi \(\Delta MAB\) đạt giá trị lớn nhất. Câu 5: (0,5 điểm) Giải phương trình: \(3x - 2\sqrt {x - 3} = 8\sqrt x - 6\) -------- Hết -------- Lời giải Câu 1: (2,5 điểm) Cho biểu thức \(A = \frac{{x - 4}}{{\sqrt x + 1}}\) và \(B = \frac{{\sqrt x + 1}}{{\sqrt x - 2}} + \frac{{\sqrt x + 2}}{{1 - \sqrt x }} + \frac{{\sqrt x - 4}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x - 2} \right)}}\) a) Tính giá trị của biểu thức \(A\) khi \(x = 16\). b) Rút gọn biểu thức \(B\). c) Tìm \(x\) để biểu thức \(M = A.B\) nhận giá trị nguyên. Phương pháp giải a) Tìm ĐKXĐ của biểu thức \(A\) và biểu thức \(B\) Với \(x = 16\) (tmđk) thay vào biểu thức \(A\) và tính. b) Xác định mẫu thức chung Thực hiện các phép tính với các phân thức đại số c) Tìm miền chặn của biểu thức \(M\) để tìm được giá trị \(M\) nguyên Với \(M\) nguyên tìm được \(x\) thỏa mãn Lời giải ĐKXĐ: \(x \ge 0;x \ne 1;x \ne 4\) a) Với \(x = 16\) (tmđk) thay vào \(A\) ta được: \(A = \frac{{16 - 4}}{{\sqrt {16} + 1}} = \frac{{12}}{{4 + 1}} = \frac{{12}}{5}\) Vậy \(x = 16\) thì \(A = \frac{{12}}{5}\) b) \(B = \frac{{\sqrt x + 1}}{{\sqrt x - 2}} + \frac{{\sqrt x + 2}}{{1 - \sqrt x }} + \frac{{\sqrt x - 4}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x - 2} \right)}}\) với \(x \ge 0;x \ne 1;x \ne 4\) \(\begin{array}{l} = \frac{{\sqrt x + 1}}{{\sqrt x - 2}} - \frac{{\sqrt x + 2}}{{\sqrt x - 1}} + \frac{{\sqrt x - 4}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x - 2} \right)}}\\ = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right) - \left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right) + \left( {\sqrt x - 4} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x - 2} \right)}}\\ = \frac{{x - 1 - x + 4 + \sqrt x - 4}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x - 2} \right)}}\\ = \frac{{\sqrt x - 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x - 2} \right)}}\\ = \frac{1}{{\sqrt x - 2}}\end{array}\) Vậy \(B = \frac{1}{{\sqrt x - 2}}\) với \(x \ge 0;x \ne 1;x \ne 4\) c) Ta có: \(M = A.B = \frac{{x - 4}}{{\sqrt x + 1}}.\frac{1}{{\sqrt x - 2}} = \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}} = \frac{{\sqrt x + 2}}{{\sqrt x + 1}}\) \(M = \frac{{\sqrt x + 2}}{{\sqrt x + 1}} = \frac{{\sqrt x + 1 + 1}}{{\sqrt x + 1}} = 1 + \frac{1}{{\sqrt x + 1}}\) Vì \(x \ge 0 \Rightarrow 1 + \frac{1}{{\sqrt x + 1}} > 1\) \( \Rightarrow M > 1\) Vì \(x \ge 0 \Rightarrow \sqrt x + 1 \ge 1\) \(\begin{array}{l} \Rightarrow \frac{1}{{\sqrt x + 1}} \le 1\\ \Rightarrow 1 + \frac{1}{{\sqrt x + 1}} \le 2\\ \Rightarrow M \le 2\end{array}\) Vậy \(1 < M \le 2\), mà \(M\) là số nguyên nên \(M = 2\) * Với \(M = 2 \Leftrightarrow \frac{{\sqrt x + 2}}{{\sqrt x + 1}} = 2\) \(\begin{array}{l} \Leftrightarrow 2\left( {\sqrt x + 1} \right) = \sqrt x + 2\\ \Leftrightarrow 2\sqrt x + 2 = \sqrt x + 2\\ \Leftrightarrow \sqrt x = 0\\ \Leftrightarrow x = 0\left( {tmdk} \right)\end{array}\) Vậy \(x = 0\) thì \(M = A.B\) là số nguyên. Câu 2: (2 điểm) Cho hàm số \(y = \left( {1 - m} \right)x + m + 2\) (với \(m\) là tham số) có đồ thị là đường thẳng \(d\). Xác định \(m\) để: a) Đường thẳng \(d\) cắt trục hoành tại điểm có hoành độ bằng 2. b) Đường thẳng \(d\) song song với đường thẳng \(y = 2x - 1\) c) Đường thẳng \(d\) cắt trục \(Ox,Oy\) lần lượt tại hai điểm \(A,B\) sao cho tam giác \(AOB\) vuông cân. Phương pháp giải a) Thay tọa độ \(\left( {2;0} \right)\) vào hàm số của đường thẳng \(d \Rightarrow \) tìm được \(m\) b) Đường thẳng \(\left( d \right):y = ax + b\) song song với đường thẳng \(\left( {d'} \right):y = a'x + b'\) khi và chỉ khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\). c) Tìm tọa độ điểm \(A;B\) Tính \(OA = OB\) \(\Delta AOB\) vuông cân cần thêm điều kiện: \(OA = OB\) Lời giải a) Đường thẳng \(d\) cắt trục hoành tại điểm có hoành độ bằng 2 nên ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\,2\left( {1 - m} \right) + m + 2 = 0\\ \Leftrightarrow 2 - 2m + m + 2 = 0\\ \Leftrightarrow - m + 4 = 0\\ \Leftrightarrow m = 4\end{array}\) Vậy \(m = 4\) b) Đường thẳng \(d\) song song với đường thẳng \(y = 2x - 1\) khi và chỉ khi \(\left\{ \begin{array}{l}1 - m = 2\\m + 2 \ne - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - 1\\m \ne - 3\end{array} \right. \Leftrightarrow m = - 1\) Vậy \(m = - 1\) c) *Với \(m = 1\), ta có: \(d:y = 3\) là đường thẳng song song với trục hoành \(Ox\) \( \Rightarrow m = 1\) (ktm) *Với \(m = 1\), ta có: \(y = \left( {1 - m} \right)x + m + 2\) là đường thẳng cắt trục \(Ox,Oy\) Đường thẳng \(d\) cắt \(Ox\) tại \(A \Rightarrow A\left( {\frac{{m + 2}}{{m - 1}};0} \right)\) Do đó, \(OA = \left| {\frac{{m + 2}}{{m - 1}}} \right|\) Đường thẳng \(d\) cắt \(Oy\) tại \(B \Rightarrow B\left( {0;m + 2} \right)\) Do đó, \(OB = \left| {m + 2} \right|\) Vì \(\Delta OAB\) vuông cân ở \(O \Rightarrow OA = OB\) \(\begin{array}{l} \Leftrightarrow \left| {\frac{{m + 2}}{{m - 1}}} \right| = \left| {m + 2} \right|\\ \Leftrightarrow \left| {m + 2} \right|\left( {\frac{1}{{\left| {m - 1} \right|}} - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\left| {m + 2} \right| = 0\\\frac{1}{{\left| {m - 1} \right|}} = 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m + 2 = 0\\\left| {m - 1} \right| = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 2\\\left[ \begin{array}{l}m - 1 = 1\\m - 1 = - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 2\left( {tmdk} \right)\\m = 2\left( {tmdk} \right)\\m = 0\left( {tmdk} \right)\end{array} \right.\end{array}\) Vậy \(m \in \left\{ { - 2;0;2} \right\}\) Câu 3: (1,5 điểm) 1) Giải hệ phương trình: \(\left\{ \begin{array}{l}2\left| {x - 1} \right| - \frac{3}{{\sqrt {y + 3} }} = - 3\\\left| {x - 1} \right| + \frac{1}{{\sqrt {y + 3} }} = 1\end{array} \right.\) 2) Giá niêm yết của các chiếc tủ lạnh cùng loại trong siêu thị là như nhau. Gian hàng A bán với giá khuyên mãi \(20\% \). Gian hàng B, lần 1 giảm giá \(10\% \) cũng bán được chưa được nên giảm tiếp \(10\% \) nữa so với giá đã giảm lần thứ nhất. Nếu là người mua hàng, để mua được giá rẻ hơn em sẽ chọn mua ở gian hàng nào? Vì sao? Phương pháp giải 1) Đặt \(\left\{ \begin{array}{l}\left| {x - 1} \right| = a\left( {a \ge 0} \right)\\\frac{1}{{\sqrt {y + 3} }} = b\left( {b > 0} \right)\end{array} \right.\), khi đó có hệ phương trình bậc nhất hai ẩn \(a,b\) Sử dụng phương pháp cộng đại số, tìm \(a,b\) (đối chiếu điều kiện) Từ \(a,b\) tìm được, tìm được nghiệm của hệ phương trình \(\left( {x;y} \right)\) 2) Tính giá bán của gian hàng A sau giảm Tính giá bán của gian hàng B sau giảm So sánh và kết luận Lời giải ĐKXĐ: \(y > - 3\) Đặt \(\left\{ \begin{array}{l}\left| {x - 1} \right| = a\left( {a \ge 0} \right)\\\frac{1}{{\sqrt {y + 3} }} = b\left( {b > 0} \right)\end{array} \right.\), khi đó hệ phương trình ban đầu trở thành: \(\left\{ \begin{array}{l}2a - 3b = - 3\\a + b = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a - 3b = - 3\\3a + 3b = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5a = 0\\a + b = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\left( {tmdk} \right)\\b = 1\left( {tmdk} \right)\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}\left| {x - 1} \right| = 0\\\frac{1}{{\sqrt {y + 3} }} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 0\\\sqrt {y + 3} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y + 3 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 2\end{array} \right.\) Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1; - 2} \right)\) 2) Gọi giá niêm yết chiếc tủ lạnh là: \(x\) đồng. Gian hàng A bán với giá là: \(100\% x - 20\% x = 80\% x\) (đồng) Gian hàng B bán với giá giảm lần 1 là: \(100\% x - 10\% x = 90\% x\) (đồng) Gian hàng B bán với giá giảm lần 2 là: \(90\% x - 10\% .90\% x = 81\% x\) (đồng) Vậy gian hàng A có giá bán rẻ hơn so với gian hàng B nên chọn mua ở gian hàng A. Câu 4: (3,5 điểm) Cho đường tròn \(\left( {O;R} \right)\) có hai đường kính \(AB\) và \(CD\) vuông góc với nhau. Điểm \(E\) thay đổi thuộc đoạn \(OC,\) nối \(AE\) cắt đường tròn \(\left( O \right)\) tại \(M\). a) Chứng minh 4 điểm \(O,B,M,E\) cùng nằm trên một đường tròn. b) Chứng minh \(AE.AM\) không phụ thuộc vào vị trí của điểm \(E\) trên đoạn \(OC\). c) Xác định vị trí của \(E\) trên đoạn \(OC\) để \(MA = 2MB\). d) Xác định vị trí của điểm \(E\) trên đoạn \(OC\) để chu vi \(\Delta MAB\) đạt giá trị lớn nhất. Phương pháp giải a) \(O,M\) cùng thuộc đường tròn đường kính \(BE\) b) $\Delta AOE\backsim \Delta AMB\left( g.g \right)$\( \Rightarrow AE.AM = 2{R^2}\) không đổi c) $\Delta AOE\backsim \Delta AMB\left( cmt \right)$\( \Rightarrow OE = \frac{{OC}}{2}\) \( \Rightarrow E\) là trung điểm của \(OC\) d) Ta có: \({C_{\Delta MAB}} = AB + AM + MB = 2R + AM + MB\) Vì \(AB = 2R\) không đổi nên \({C_{\Delta MAB}}\max \Leftrightarrow \left( {AM + MB} \right)\max \) Áp dụng bất đẳng thức Bunhiacopxki tìm \(\left( {AM + MB} \right)\max \) Lời giải
a) Ta có: \(AB \bot CD\) tại \(O \Rightarrow \angle BOC = {90^0} \Rightarrow \angle BOE = {90^0}\) \( \Rightarrow \Delta BOE\) vuông tại \(O \Rightarrow O\) thuộc đường tròn đường kính \(BE\) \(M\) thuộc đường tròn đường kính \(AB \Rightarrow \angle AMB = {90^0}\) \( \Rightarrow \Delta BME\) vuông tại \(M \Rightarrow M\) thuộc đường tròn đường kính \(BE\) Vậy \(O,M\) thuộc đường tròn đường kính \(BE\) nên bốn điểm \(B,M,E,O\) cùng thuộc một đường tròn. b) Xét \(\Delta AOE\) và \(\Delta AMB\) có: \(\left. \begin{array}{l}\angle BAM\,\,\,chung\\\angle AOE = \angle AMB = {90^0}\end{array} \right\}\)$\Rightarrow \Delta AOE\backsim \Delta AMB\left( g.g \right)$ \(\begin{array}{l} \Rightarrow \frac{{AE}}{{AB}} = \frac{{AO}}{{AM}}\\ \Rightarrow AE.AM = AO.AB = R.2R = 2{R^2}\end{array}\) Mà \(R\) không đổi nên \(AE.AM\) không đổi khi \(E\) thay đổi. c) Ta có: $\Delta AOE\backsim \Delta AMB\left( cmt \right)$ \(\begin{array}{l} \Rightarrow \frac{{AO}}{{AM}} = \frac{{OE}}{{MB}}\\ \Rightarrow OE = \frac{{AO.BM}}{{AM}} = \frac{{R.BM}}{{2BM}} = \frac{R}{2} = \frac{{OC}}{2}\end{array}\) Lại có: \(E \in OC\) \( \Rightarrow E\) là trung điểm của \(OC\) d) Ta có: \({C_{\Delta MAB}} = AB + AM + MB = 2R + AM + MB\) Vì \(AB = 2R\) không đổi nên \({C_{\Delta MAB}}\max \Leftrightarrow \left( {AM + MB} \right)\max \) Ta có: \({\left( {MA + MB} \right)^2} \le \left( {{1^2} + {1^2}} \right)\left( {M{A^2} + M{B^2}} \right)\) \( \Leftrightarrow {\left( {MA + MB} \right)^2} \le 2A{B^2}\) (vì \(\Delta AMB\) vuông tại \(M \Rightarrow A{B^2} = M{A^2} + M{B^2}\) (định lý Py – ta – go) \(\begin{array}{l} \Leftrightarrow {\left( {MA + MB} \right)^2} \le 2{\left( {2R} \right)^2}\\ \Leftrightarrow MA + MB \le 2\sqrt 2 R\\ \Leftrightarrow MA + MB + AB \le 2\sqrt 2 R + AB\\ \Leftrightarrow {C_{\Delta MAB}} \le 2\sqrt 2 R + 2R\\ \Leftrightarrow {C_{\Delta MAB}} \le 2R\left( {\sqrt 2 + 1} \right)\end{array}\) Dấu “=” xảy ra \( \Leftrightarrow AM = BM\) Mà \(\Delta MAB\) vuông tại \(M\) \( \Rightarrow \Delta MAB\) là tam giác vuông cân \( \Rightarrow E \equiv C\) Câu 5: (0,5 điểm) Giải phương trình: \(3x - 2\sqrt {x - 3} = 8\sqrt x - 6\) Phương pháp giải Sử dụng hằng đẳng thức: \({a^2} + 2ab + {b^2} = {\left( {a + b} \right)^2}\,;\,\,{a^2} - 2ab + {b^2} = {\left( {a - b} \right)^2}\) Giải phương trình: \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\left( {g\left( x \right) \ge 0} \right)\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\) Lời giải ĐKXĐ: \(x \ge 3\) \(\begin{array}{l}\,\,\,\,\,\,\,\,3x - 2\sqrt {x - 3} = 8\sqrt x - 6\\ \Leftrightarrow 8\sqrt x + 2\sqrt {x - 3} - 6 - 3x = 0\\ \Leftrightarrow - \left( {x - 3} \right) + 2\sqrt {x - 3} - 1 - 2\left( {x - 4\sqrt x + 4} \right) - 3 + 1 + 8 - 6 = 0\\ \Leftrightarrow - {\left( {\sqrt {x - 3} - 1} \right)^2} - 2{\left( {\sqrt x - 2} \right)^2} = 0\\ \Leftrightarrow {\left( {\sqrt {x - 3} - 1} \right)^2} + 2{\left( {\sqrt x - 2} \right)^2} = 0\end{array}\) Vì \(\left\{ \begin{array}{l}{\left( {\sqrt {x - 3} - 1} \right)^2} \ge 0,\forall x \ge 3\\2{\left( {\sqrt x - 2} \right)^2} \ge 0,\forall x \ge 3\end{array} \right.\) \( \Rightarrow {\left( {\sqrt {x - 3} - 1} \right)^2} + 2{\left( {\sqrt x - 2} \right)^2} \ge 0\) Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}\sqrt {x - 3} - 1 = 0\\\sqrt x - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt {x - 3} = 1\\\sqrt x = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 3 = 1\\x = 4\end{array} \right. \Leftrightarrow x = 4\left( {tmdk} \right)\) Vậy phương trình có nghiệm duy nhất \(x = 4\)
|