Đề thi kì 1 môn toán lớp 9 năm 2019 - 2020 phòng GDĐT Bắc Từ LiêmTải vềGiải chi tiết đề thi kì 1 môn toán lớp 9 năm 2019 - 2020 phòng GDĐT Bắc Từ Liêm với cách giải nhanh và chú ý quan trọng Bài 1 (2,0 điểm): Cho các biểu thức: \(A = \dfrac{6}{{\sqrt x \left( {\sqrt x - 3} \right)}}\) và \(B = \dfrac{{2\sqrt x }}{{x - 9}} - \dfrac{2}{{\sqrt x + 3}}\) với \(x > 0;x \ne 9\) 1) Tính giá trị của \(A\) khi \(x = 4.\) 2) Rút gọn biểu thức \(M = A:B.\) 3) Tìm các giá trị của \(x\) để \(3\sqrt x + 5 = 2M.\) Bài 2 (2 điểm): 1) Thực hiện phép tính: \(3\sqrt 8 - \sqrt {50} - \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} .\) 2) Giải các phương trình sau: a) \(\sqrt {{x^2} - 6x + 9} = 1\) b) \(2\sqrt {12x} - 3\sqrt {3x} + 4\sqrt {48x} = 17.\) Bài 3 (2 điểm): Cho hàm số \(y = \left( {m + 1} \right)x + 6\,\,\,\left( 1 \right)\) với \(m \ne - 1\) 1) Vẽ đồ thị hàm số \(\left( 1 \right)\) khi \(m = 2.\) 2) Gọi đồ thị của hàm số \(\left( 1 \right)\) là đường thẳng \(\left( d \right),\) tìm \(m\) để đường thẳng \(\left( d \right)\) cắt đường thẳng \(y = 5x + m - 2\) tại một điểm nằm trên trục tung. 3) Tìm \(m\) để khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(\left( d \right)\) bằng \(3\sqrt 2 .\) Bài 4 (3,5 điểm): Cho điểm \(M\) nằm ngoài đường tròn \(\left( {O;R} \right)\). Từ \(M\) kẻ các tiếp tuyến \(MA,MB\) tới đường tròn tâm \(O\) (\(A,B\) là các tiếp điểm). Gọi \(H\) là giao điểm của \(MO\) với \(AB.\) 1) Chứng minh rằng bốn điểm \(M,A,O,B\) cùng thuộc một đường tròn. 2) Chứng minh rằng \(MO \bot AB\) tại \(H.\) 3) Nếu \(OM = 2R\) hãy tính độ dài \(MA\) theo \(R\) và số đo các góc \(\angle AMB,\angle AOB?\) 4) Kẻ đường kính \(AD\) của đường tròn \(\left( O \right),\,\,MD\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(C.\) Chứng minh rằng \(\angle MHC = \angle ADC.\) Bài 5 (0,5 điểm): Cho \(x,y\) là các số dương thỏa mãn \(x \ge 2y.\) Tìm giá trị nhỏ nhất của biểu thức \(M\) với \(M = \dfrac{{{x^2} + {y^2}}}{{xy}}.\)
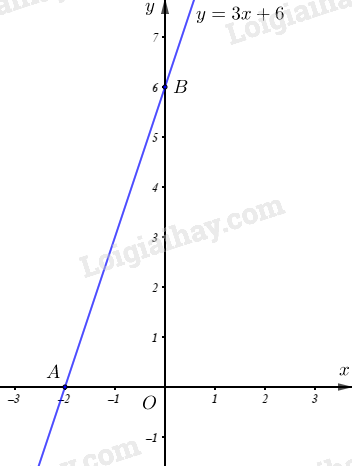
HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện: Ban chuyên môn HocTot.Nam.Name.Vn Bài 1 (VD): Phương pháp: 1) Thay giá trị của \(x = 4\) (tmđk) vào biểu thức \(A\) để tính. 2) Quy đồng, rút gọn phân thức. 3) Biến đổi để đưa về phương trình tích \(f\left( x \right).g\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\g\left( x \right) = 0\end{array} \right.\) Cách giải: Cho các biểu thức: \(A = \dfrac{6}{{\sqrt x \left( {\sqrt x - 3} \right)}}\) và \(B = \dfrac{{2\sqrt x }}{{x - 9}} - \dfrac{2}{{\sqrt x + 3}}\) với \(x > 0;x \ne 9\) 1) Tính giá trị của \(A\) khi \(x = 4.\) Với \(x = 4\) thỏa mãn điều kiện \(x > 0\,\,;\,\,x \ne 9\) Thay \(x = 4\) vào biểu thức \(A = \dfrac{6}{{\sqrt x \left( {\sqrt x - 3} \right)}}\) ta được: \(A = \dfrac{6}{{\sqrt 4 .\left( {\sqrt 4 - 3} \right)}} = \dfrac{6}{{2.\left( {2 - 3} \right)}} = \dfrac{6}{{ - 2}} = - 3\) Vậy khi \(x = 4\) thì \(A = - 3.\) 2) Rút gọn biểu thức \(M = A:B.\) Điều kiện: \(x > 0\,\,;\,\,x \ne 9\) \(\begin{array}{l}M = A:B = \dfrac{6}{{\sqrt x \left( {\sqrt x - 3} \right)}}:\left( {\dfrac{{2\sqrt x }}{{x - 9}} - \dfrac{2}{{\sqrt x + 3}}} \right)\\\,\,\,\,\,\,\, = \dfrac{6}{{\sqrt x \left( {\sqrt x - 3} \right)}}:\dfrac{{2\sqrt x - 2\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\\\,\,\,\,\,\,\, = \dfrac{6}{{\sqrt x \left( {\sqrt x - 3} \right)}}:\dfrac{6}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\\\,\,\,\,\,\,\, = \dfrac{6}{{\sqrt x \left( {\sqrt x - 3} \right)}}.\dfrac{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}{6}\\\,\,\,\,\,\,\, = \dfrac{{\sqrt x + 3}}{{\sqrt x }}\end{array}\) Vậy \(M = \dfrac{{\sqrt x + 3}}{{\sqrt x }}.\) 3) Tìm các giá trị của \(x\) để \(3\sqrt x + 5 = 2M.\) Điều kiện: \(x > 0.\) \(\begin{array}{l}3\sqrt x + 5 = 2M \Leftrightarrow 3\sqrt x + 5 = 2.\dfrac{{\sqrt x + 3}}{{\sqrt x }}\\ \Leftrightarrow \sqrt x \left( {3\sqrt x + 5} \right) = 2\sqrt x + 6\\ \Leftrightarrow 3x + 5\sqrt x = 2\sqrt x + 6 \Leftrightarrow 3x + 3\sqrt x - 6 = 0\\ \Leftrightarrow x + \sqrt x - 2 = 0 \Leftrightarrow \left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt x - 1 = 0\\\sqrt x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt x = 1\\\sqrt x = - 2\,\,\,\left( {không\,thỏa\,mãn} \right)\end{array} \right.\\ \Leftrightarrow x = 1\,\,\left( {thỏa\,mãn} \right)\end{array}\) Vậy \(x = 1.\) Bài 2 (VD): Phương pháp: 1) Rút gọn căn bậc hai bằng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\;\,khi\,\,A \ge 0\\ - A\sqrt B \,\;\,khi\,\,A < 0\end{array} \right..\) 2) a) Tìm điều kiện xác định sau đó giải phương trình bằng phương pháp đưa phương trình về dạng \(\left| A \right| = m\,\left( {m \ge 0} \right) \Leftrightarrow \left[ \begin{array}{l}A = m\\A = - m\end{array} \right.\) b) Tìm điều kiện xác định của phương trình sau đó dùng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\;\,khi\,\,A \ge 0\\ - A\sqrt B \,\;\,khi\,\,A < 0\end{array} \right.\) để giải phương trình. Cách giải: 1) Thực hiện phép tính: \(3\sqrt 8 - \sqrt {50} - \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} .\) \(\begin{array}{l}3\sqrt 8 - \sqrt {50} - \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} \\ = 3\sqrt {{2^2}.2} - \sqrt {{5^2}.2} - \left| {\sqrt 2 - 1} \right|\\ = 3.2\sqrt 2 - 5\sqrt 2 - \left( {\sqrt 2 - 1} \right)\\ = 6\sqrt 2 - 5\sqrt 2 - \sqrt 2 + 1\\ = 1\end{array}\) 2) Giải các phương trình sau: a) \(\sqrt {{x^2} - 6x + 9} = 1\) Điều kiện xác định: \(x \in \mathbb{R}\) \(({x^2} - 6x + 9 \ge 0 \Leftrightarrow {\left( {x - 3} \right)^2} \ge 0\) đúng với mọi \(x \in \mathbb{R}\,)\) \(\begin{array}{l}\sqrt {{x^2} - 6x + 9} = 1 \Leftrightarrow \sqrt {{{\left( {x - 3} \right)}^2}} = 1\\ \Leftrightarrow \left| {x - 3} \right| = 1 \Leftrightarrow \left[ \begin{array}{l}x - 3 = 1\\x - 3 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 2\end{array} \right.\,\,\,\left( {tmdk} \right)\end{array}\) Vậy \(S = \left\{ {2;4} \right\}.\) b) \(2\sqrt {12x} - 3\sqrt {3x} + 4\sqrt {48x} = 17.\) Điều kiện xác định: \(x \ge 0\) \(\begin{array}{l}2\sqrt {12x} - 3\sqrt {3x} + 4\sqrt {48x} = 17\\ \Leftrightarrow 2\sqrt {{2^2}.3x} - 3\sqrt {3x} + 4\sqrt {{4^2}.3x} = 17\\ \Leftrightarrow 2.2\sqrt {3x} - 3\sqrt {3x} + 4.4\sqrt {3x} = 17\\ \Leftrightarrow 4\sqrt {3x} - 3\sqrt {3x} + 16\sqrt {3x} = 17\\ \Leftrightarrow 17\sqrt {3x} = 17 \Leftrightarrow \sqrt {3x} = 1\\ \Leftrightarrow 3x = 1 \Leftrightarrow x = \dfrac{1}{3}\,\,\left( {tmdk} \right)\end{array}\) Vậy \(S = \left\{ {\dfrac{1}{3}} \right\}.\) Bài 3 (VD): Phương pháp: 1) Vẽ đường thẳng trong mặt phẳng Oxy bằng cách xác định hai điểm mà đường thẳng đi qua. 2) Để hai đường thẳng \(\left( d \right):y = ax + b\) và \(\left( {d'} \right):y = a'x + b'\) cắt nhau tại một điểm trên trục tung thì \(a \ne a'\) và phương trình hoành độ giao điểm của hai đường thẳng có nghiệm \(x = 0\). 3) Tìm tọa độ giao điểm của đồ thị hàm số với trục hoành và trục tung. Sau đó sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách. Cách giải: Cho hàm số \(y = \left( {m + 1} \right)x + 6\,\,\,\left( 1 \right)\) với \(m \ne - 1\) 1) Vẽ đồ thị hàm số \(\left( 1 \right)\) khi \(m = 2.\) Với \(m = 2\) thì \(y = 3x + 6\) Vẽ đồ thị hàm số: \(y = 3x + 6:\) +) Giao điểm \(A\) của đường thẳng \(y = 3x + 6\) với trục \(Ox\) là: \({y_A} = 0 \Rightarrow 3{x_A} + 6 = 0\, \Rightarrow {x_A} = - 2\, \Rightarrow A\left( { - 2;0} \right)\) +) Giao điểm \(B\) của đường thẳng \(y = 3x + 6\) với trục \(Oy\) là: \({x_B} = 0 \Rightarrow {y_B} = 3{x_B} + 6 = 6\, \Rightarrow B\left( {0;6} \right)\) +) Vẽ đường thẳng \(y = 3x + 6\) trong mặt phẳng \(Oxy:\) Ta có đường thẳng \(y = 3x + 6\) đi qua hai điểm \(A\left( { - 2;0} \right);B\left( {0;6} \right)\) nên đường thẳng \(y = 3x + 6\) chính là đường thẳng \(AB.\) Ta có hình vẽ:
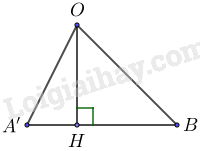
2) Gọi đồ thị của hàm số \(\left( 1 \right)\) là đường thẳng \(\left( d \right),\) tìm \(m\) để đường thẳng \(\left( d \right)\) cắt đường thẳng \(y = 5x + m - 2\) tại một điểm nằm trên trục tung. Để \(d:\,\,y = \left( {m + 1} \right)x + 6\) cắt đường thẳng \(y = 5x + m - 2\) tại một điểm nằm trên trục tung thì \(m + 1 \ne 5\) và phương trình hoành độ giao điểm của hai đường thẳng có nghiệm \(x = 0\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m + 1 \ne 5\\\left( {m + 1} \right).0 + 6 = 5.0 + m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 4\\6 = m - 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 4\\m = 8\end{array} \right. \Leftrightarrow m = 8\,\,\,\left( {tmdk\,\,m \ne - 1} \right)\end{array}\) Vậy \(m = 8\) là giá trị cần tìm. 3) Tìm \(m\) để khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(\left( d \right)\) bằng \(3\sqrt 2 .\) Đồ thị hàm số \(y = \left( {m + 1} \right)x + 6\) với \(m \ne - 1\) là đường thẳng cắt \(Ox\) tại điểm \(A'\left( { - \dfrac{6}{{m + 1}};0} \right)\) và cắt \(Oy\) tại điểm \(B\left( {0;6} \right)\) Suy ra: \(OA' = \left| {\dfrac{{ - 6}}{{m + 1}}} \right| = \dfrac{6}{{\left| {m + 1} \right|}}\) và \(OB = \left| 6 \right| = 6\) Kẻ \(OH \bot A'B\) tại \(H\) thì \(OH\) chính là khoảng cách từ \(O\) đến đường thẳng \(\left( d \right)\)
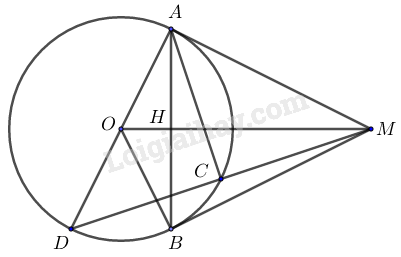
Ta có: \(\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{OA{'^2}}} + \dfrac{1}{{O{B^2}}} \Leftrightarrow \dfrac{1}{{{{\left( {3\sqrt 2 } \right)}^2}}} = \dfrac{1}{{{{\left( {\dfrac{6}{{\left| {m + 1} \right|}}} \right)}^2}}} = \dfrac{1}{{{6^2}}}\\ \Leftrightarrow \dfrac{1}{{16}} = \dfrac{1}{{\dfrac{{36}}{{{{\left( {m + 1} \right)}^2}}}}} + \dfrac{1}{{36}} \Leftrightarrow \dfrac{1}{{18}} = \dfrac{{{{\left( {m + 1} \right)}^2} + 1}}{{36}}\\ \Leftrightarrow \dfrac{2}{{36}} = \dfrac{{{m^2} + 2m + 1 + 1}}{{36}} \Leftrightarrow 2 = {m^2} + 2m + 2\\ \Leftrightarrow {m^2} + 2m = 0 \Leftrightarrow m\left( {m + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\\m + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = - 2\end{array} \right.\,\,\,\left( {tmdk} \right)\end{array}\) Vậy \(m \in \left\{ {0; - 2} \right\}\) là giá trị cần tìm. Bài 4 (VD): Phương pháp: 1) Sử dụng: Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền. 2) Sử dụng: Tính chất hai tiếp tuyến cắt nhau 3) Sử dụng: Định lý Pytago, tỉ số lượng giác của góc nhọn và tính chất hai tiếp tuyến cắt nhau 4) Sử dụng: Hệ thức lượng trong tam giác vuông, chứng minh hai tam giác \(\Delta MHC\) và \(\Delta MDO\) đồng dạng từ đó suy ra các góc tương ứng bằng nhau. Cách giải: Cho điểm \(M\) nằm ngoài đường tròn \(\left( {O;R} \right)\). Từ \(M\) kẻ các tiếp tuyến \(MA,MB\) tới đường tròn tâm \(O\) (\(A,B\) là các tiếp điểm). Gọi \(H\) là giao điểm của \(MO\) với \(AB.\)
1) Chứng minh rằng bốn điểm \(M,A,O,B\) cùng thuộc một đường tròn. \(MA,MB\) là các tiếp tuyến của \(M\) đến đường tròn \(\left( {O;R} \right)\) \( \Rightarrow \angle OAM = \angle OBM = {90^0}\) \( \Rightarrow A,B\) thuộc đường tròn đường kính \(OM\) \( \Rightarrow M,A,O,B\) cùng thuộc một đường tròn (đpcm). 2) Chứng minh rằng \(MO \bot AB\) tại \(H.\) \(MA,MB\) là các tiếp tuyến của \(M\) đến đường tròn \(\left( {O;R} \right)\) \( \Rightarrow MA = MB\) và \(MO\) là tia phân giác của \(\angle AMB\) (tính chất hai tiếp tuyến cắt nhau) Do đó \(MO\) đồng thời là đường cao của tam giác cân \(AMB\) Suy ra \(MO \bot AB\) tại \(H.\) 3) Nếu \(OM = 2R\) hãy tính độ dài \(MA\) theo \(R\) và số đo các góc \(\angle AMB,\angle AOB?\) \(\angle OAM = {90^0}\,\, \Rightarrow \Delta OAM\) vuông tại \(A\) \( \Rightarrow O{M^2} = O{A^2} + M{A^2}\,\,\) (định lý Py-ta-go) \( \Rightarrow M{A^2} = \sqrt {O{M^2} - O{A^2}} = \sqrt {{{\left( {2R} \right)}^2} - {R^2}} = R\sqrt 3 \) Áp dụng tỉ số lượng giác cho tam giác vuông \(OAM\) ta được: \(\sin \angle AOM = \dfrac{{AM}}{{OM}} = \dfrac{{R\sqrt 3 }}{{2R}} = \dfrac{{\sqrt 3 }}{2}\,\, \Rightarrow \angle AOM = {60^0}\) Do \(MA,MB\) là các tiếp tuyến của \(M\) đến đường tròn \(\left( {O;R} \right)\) \( \Rightarrow OM\) là tia phân giác của \(\angle AOB\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow \angle AOB = 2.\angle AOM = {2.60^0} = {120^0}\) 4) Kẻ đường kính \(AD\) của đường tròn \(\left( O \right),\,\,MD\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(C.\) Chứng minh rằng \(\angle MHC = \angle ADC.\) \(\Delta OAM\) vuông tại \(A\) có \(AH \bot OM\,\, \Rightarrow A{M^2} = MH.MO\,\,\,\left( 1 \right)\) Ta có: \(\angle ACD = {90^0}\) (do \(AD\) là đường kính) \( \Rightarrow AC \bot DM\) \(\angle OAM = {90^0}\) hay \(\angle DAM = {90^0}\,\, \Rightarrow \Delta ADM\) vuông tại \(A\) có \(AC \bot DM\,\, \Rightarrow A{M^2} = MC.MD\,\,\,\left( 2 \right)\) Từ \(\left( 1 \right),\left( 2 \right)\,\, \Rightarrow MH.MO = MC.MD\,\,\left( { = A{M^2}} \right)\,\, \Rightarrow \dfrac{{MH}}{{MD}} = \dfrac{{MC}}{{MO}}\) Xét \(\Delta MHC\) và \(\Delta MDO\) có: \(\begin{array}{l}\angle OMD\,\,\,chung\\\dfrac{{MH}}{{MD}} = \dfrac{{MC}}{{MO}}\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta MHC \backsim \Delta MDO\,\,\,\left( {c - g - c} \right)\\ \Rightarrow \angle MHC = \angle ADC\,\,\,\left( {dpcm} \right)\end{array}\) Bài 5 (VDC): Phương pháp: Áp dụng bất đẳng thức Cô-si: với \(a,b > 0\) thì \(a + b \ge 2\sqrt {ab} \) Cách giải: Cho \(x,y\) là các số dương thỏa mãn \(x \ge 2y.\) Tìm giá trị nhỏ nhất của biểu thức \(M\) với \(M = \dfrac{{{x^2} + {y^2}}}{{xy}}.\) Ta có: \(x,y > 0\,\,;\,\,x \ge 2y\,\, \Rightarrow \dfrac{x}{y} \ge 2\) \(\begin{array}{l}M = \dfrac{{{x^2} + {y^2}}}{{xy}} = \dfrac{{{x^2}}}{{xy}} + \dfrac{{{y^2}}}{{xy}} = \dfrac{x}{y} + \dfrac{y}{x} = \dfrac{x}{{4y}} + \dfrac{y}{x} + \dfrac{{3x}}{{4y}}\\\,\,\,\,\,\,\, \ge 2\sqrt {\dfrac{x}{{4y}}.\dfrac{y}{x}} + \dfrac{{3x}}{{4y}} = 2.\sqrt {\dfrac{1}{4}} + \dfrac{3}{4}.2 = \dfrac{5}{2}\end{array}\) Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}\dfrac{x}{{4y}} = \dfrac{y}{x}\\\dfrac{x}{y} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} = 4{y^2}\\x = 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 2y\\x = - 2y\end{array} \right.\\x = 2y\end{array} \right.\,\, \Leftrightarrow x = 2y\) Vậy \({M_{\min }} = \dfrac{5}{2}\) khi \(x = 2y.\) HẾT HocTot.Nam.Name.Vn
|