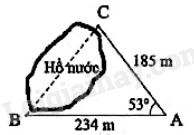
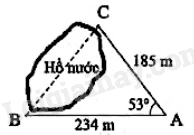
Đề kiểm tra giữa kì 1 Toán 9 - Đề số 15 có lời giải chi tiếtTải về Đề kiểm tra giữa kì 1 Toán 9 - Đề số 15 có lời giải chi tiết Đề bài Câu 1: Rút gọn các biểu thức sau: a) \(A = \sqrt {{{(3 - \sqrt 5 )}^2}} + \frac{3}{4}\sqrt {80} - 6\) b) \(B = \frac{{\sqrt {18} }}{{\sqrt 6 }} + \frac{4}{{\sqrt 5 - 1}} - \frac{{3 + \sqrt 3 }}{{1 + \sqrt 3 }}\) c) \(C = {\sin ^2}{33^0} - \frac{{\tan {{29}^0}}}{{\cot {{61}^0}}} - \frac{1}{2} \cdot {\cos ^2}{60^0} + {\sin ^2}{57^0}\) Câu 2: Giải các phương trình sau: a) \(9\sqrt {x + 2} - \frac{1}{3}\sqrt {9x + 18} = 24\) b) \(\sqrt {{x^2} - 6x + 9} - 2\sqrt {x - 3} = 0\) Câu 3: Cho biểu thức \(P = \left( {\frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}} - \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x {\rm{ \;}} + 1}} + \frac{2}{{x - 1}}} \right)\). a) Rút gọn \(P\) b) Tính giá trị của \(P\) biết \(x = 7 - 4\sqrt 3 \) c) Tìm \(x\) biết \(P = \frac{3}{2}\) Câu 4: 1) Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 6cm và diện tích tam giác ABC bằng \(24c{m^2}\). Tính độ dài các đoạn thẳng AC,BC,AH. 2) Tính khoảng cách giữa hai điểm B và C, biết rằng từ vị trị A ta đo được \(AB = 234{\mkern 1mu} m,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} AC = 185{\mkern 1mu} m\) và \(\widehat {BAC} = {53^0}\) (kết quả tính bằng mét và làm tròn đến hàng đơn vị).
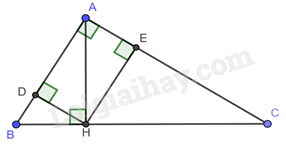
3) Cho tam giác ABC vuông tại \(A{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {AB < AC} \right)\) với đường cao AH. Goi D và E lần lượt là hình chiếu của H trên AB và AC. Chứng minh: a) \(AB.AD = AC.AE\) b) \(\frac{{A{B^2}}}{{A{C^2}}} = \frac{{BH}}{{CH}}\) Câu 5: Cho các số thực \(x,y > 0\) thỏa mãn \(\sqrt x + \sqrt y = 2\). Tìm giá trị nhỏ nhất của biều thức: \(P = x + y - 2022\sqrt {xy} \) -------- Hết -------- Lời giải chi tiết Câu 1: Rút gọn các biểu thức sau: a) \(A = \sqrt {{{(3 - \sqrt 5 )}^2}} + \frac{3}{4}\sqrt {80} - 6\) b) \(B = \frac{{\sqrt {18} }}{{\sqrt 6 }} + \frac{4}{{\sqrt 5 - 1}} - \frac{{3 + \sqrt 3 }}{{1 + \sqrt 3 }}\) c) \(C = {\sin ^2}{33^0} - \frac{{\tan {{29}^0}}}{{\cot {{61}^0}}} - \frac{1}{2} \cdot {\cos ^2}{60^0} + {\sin ^2}{57^0}\) Phương pháp: Công thức khai phương căn bậc hai, trục căn thức. Cách giải: a) \(A = \sqrt {{{(3 - \sqrt 5 )}^2}} + \frac{3}{4}\sqrt {80} - 6\)\( = \left| {3 - \sqrt 5 } \right| + \frac{3}{4}\sqrt {16.5} - 6 = 3 - \sqrt 5 + 3\sqrt 5 - 6 = 2\sqrt 5 - 3\) b) \(B = \frac{{\sqrt {18} }}{{\sqrt 6 }} + \frac{4}{{\sqrt 5 - 1}} - \frac{{3 + \sqrt 3 }}{{1 + \sqrt 3 }} = \sqrt {\frac{{18}}{6}} + \frac{{4\left( {\sqrt 5 + 1} \right)}}{{\left( {\sqrt 5 - 1} \right)\left( {\sqrt 5 + 1} \right)}} - \frac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{{\sqrt 3 + 1}} = \sqrt 3 + \sqrt 5 + 1 - \sqrt 3 = \sqrt 5 + 1\) c) \(C = {\sin ^2}{33^0} - \frac{{\tan {{29}^0}}}{{\cot {{61}^0}}} - \frac{1}{2} \cdot {\cos ^2}{60^0} + {\sin ^2}{57^0}\) \(\begin{array}{l} = {\sin ^2}{33^0} - \frac{{\tan {{29}^0}}}{{\tan {{29}^0}}} - \frac{1}{2} \cdot {\cos ^2}{60^0} + {\cos ^2}{31^0}\\ = {\sin ^2}{33^0} + {\cos ^2}{31^0} - 1 - \frac{1}{2}.{\left( {\frac{1}{2}} \right)^2} = 1 - 1 - \frac{1}{8} = - \frac{1}{8}\end{array}\) Câu 2: Giải các phương trình sau: a) \(9\sqrt {x + 2} - \frac{1}{3}\sqrt {9x + 18} = 24\) b) \(\sqrt {{x^2} - 6x + 9} - 2\sqrt {x - 3} = 0\) Phương pháp: a) Tìm điều kiện xác định, đưa các hệ số ra ngoài căn và rút gọn b) Tìm điều kiện xác định. Chuyển vế và bình phương 2 vế. Cách giải: a) \(9\sqrt {x + 2} - \frac{1}{3}\sqrt {9x + 18} = 24\) ĐK: \(x \ge - 2\). \(\begin{array}{l} \Leftrightarrow 9\sqrt {x + 2} - \sqrt {x + 2} = 24\\ \Leftrightarrow 8\sqrt {x + 2} = 24\\ \Leftrightarrow \sqrt {x + 2} = 3\\ \Leftrightarrow x + 2 = 9\end{array}\) \( \Leftrightarrow x = 7\) (TMĐK). Vậy phương trình có nghiệm \(x = 7\). b) \(\sqrt {{x^2} - 6x + 9} - 2\sqrt {x - 3} = 0\) ĐK: \(x \ge 3\). \(\begin{array}{l} \Leftrightarrow \sqrt {{x^2} - 6x + 9} = 2\sqrt {x - 3} \\ \Leftrightarrow {(x - 3)^2} = 4(x - 3)\\ \Leftrightarrow (x - 3)(x - 7) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x - 3 = 0}\\{x - 7 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 3\left( {tm} \right)}\\{x = 7\left( {tm} \right)}\end{array}} \right.} \right.\end{array}\) Phương trình có tập nghiệm là \(S = \{ 3;7\} \). Câu 3: Cho biểu thức \(P = \left( {\frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}} - \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x {\rm{ \;}} + 1}} + \frac{2}{{x - 1}}} \right)\). a) Rút gọn \(P\) b) Tính giá trị của \(P\) biết \(x = 7 - 4\sqrt 3 \) c) Tìm \(x\) biết \(P = \frac{3}{2}\) Cách giải: Cho biểu thức \(P = \left( {\frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}} - \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x {\rm{ \;}} + 1}} + \frac{2}{{x - 1}}} \right)\). a) Rút gọn \(P\) ĐKXĐ: \(x > 0,{\mkern 1mu} {\mkern 1mu} x \ne 1\). \(\begin{array}{*{20}{l}}{P = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x + 1}} + \frac{2}{{x - 1}}} \right)}\\{P = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right):\left( {\frac{1}{{\sqrt x + 1}} + \frac{2}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}} \right)}\\{P = \frac{{x - 1}}{{\sqrt x \left( {\sqrt x - 1} \right)}}:\frac{{\sqrt x - 1 + 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}}\\{P = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}}:\frac{{\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}}\\{P = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}}\\{P = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\sqrt x }}}\\{P = \frac{{x - 1}}{{\sqrt x }}}\end{array}\) b) Tính giá trị của \(P\) biết \(x = 7 - 4\sqrt 3 \) \(x = 7 - 4\sqrt 3 {\rm{ \;}} = {2^2} - 2.2\sqrt 3 {\rm{ \;}} + {\left( {\sqrt 3 } \right)^2} = {\left( {2 - \sqrt 3 } \right)^2}{\mkern 1mu} {\mkern 1mu} \left( {tmdk} \right)\) Thay vào \(P\): \(\begin{array}{*{20}{l}}{P = \frac{{\left( {7 - 4\sqrt 3 } \right) - 1}}{{\sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} }} = \frac{{6 - 4\sqrt 3 }}{{2 - \sqrt 3 }} = \frac{{\left( {6 - 4\sqrt 3 } \right).\left( {2 + \sqrt 3 } \right)}}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}}}\\{P = \frac{{12 + 6\sqrt 3 {\rm{ \;}} - 8\sqrt 3 {\rm{ \;}} - 12}}{{4 - 3}} = \frac{{ - 2\sqrt 3 }}{1} = {\rm{ \;}} - 2\sqrt 3 }\end{array}\) c) Tìm \(x\) biết \(P = \frac{3}{2}\) \(P = \frac{3}{2} \Leftrightarrow \frac{{x - 1}}{{\sqrt x }} = \frac{3}{2} \Leftrightarrow 2\left( {x - 1} \right) = 3\sqrt x {\rm{ \;}} \Leftrightarrow 2x - 3\sqrt x {\rm{ \;}} - 2 = 0\) Đặt \(\sqrt x {\rm{ \;}} = t{\mkern 1mu} {\mkern 1mu} \left( {t > 0,{\mkern 1mu} t \ne 1} \right)\). Phương trình \( \Leftrightarrow 2{t^2} - 3t - 2 = 0 \Leftrightarrow \left( {2t + 1} \right)\left( {t - 2} \right) \Leftrightarrow \left[ \begin{array}{l}t = 2\left( {tm} \right)\\t = - \frac{1}{2}\left( {ktm} \right)\end{array} \right.\) \(t = 2 \Leftrightarrow \sqrt x {\rm{ \;}} = 2 \Leftrightarrow x = 4{\mkern 1mu} {\mkern 1mu} \left( {tmdk} \right)\). Câu 4: 1) Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 6cm và diện tích tam giác ABC bằng \(24c{m^2}\). Tính độ dài các đoạn thẳng AC,BC,AH. 2) Tính khoảng cách giữa hai điểm B và C, biết rằng từ vị trị A ta đo được \(AB = 234{\mkern 1mu} m,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} AC = 185{\mkern 1mu} m\) và \(\widehat {BAC} = {53^0}\) (kết quả tính bằng mét và làm tròn đến hàng đơn vị).
3) Cho tam giác ABC vuông tại \(A{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {AB < AC} \right)\) với đường cao AH. Goi D và E lần lượt là hình chiếu của H trên AB và AC. Chứng minh: a) \(AB.AD = AC.AE\) b) \(\frac{{A{B^2}}}{{A{C^2}}} = \frac{{BH}}{{CH}}\) Cách giải: 1)
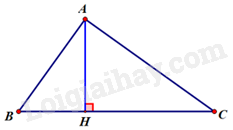
Tam giác ABC vuông tại A, khi đó ta có: \({S_{\Delta ABC}} = \frac{1}{2}AB.AC = 24 \Leftrightarrow \frac{1}{2}.6.AC = 24 \Rightarrow AC = 8cm\) Tam giác ABC vuông tại A, áp đụng dịnh lý Py – ta – go, ta có: \(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} B{C^2} = A{B^2} + A{C^2}}\\{ \Leftrightarrow B{C^2} = {6^2} + {8^2}}\\{ \Leftrightarrow B{C^2} = 100}\\{ \Rightarrow BC = 10cm}\end{array}\) Tam giác ABC có đường cao AH, khi đó ta có: \({S_{\Delta ABC}} = \frac{1}{2}AH.BC = 24 \Leftrightarrow \frac{1}{2}AH.10 = 24 \Leftrightarrow AH = 4,8cm\) 2) Từ C, dựng đường vuông góc với AB, cắt AB tại D. Khi đó ta có: CD là đường cao của \(\Delta ABC.\) Áp dụng tỉ số lượng giác của góc nhọn trong \(\Delta ACD\) vuông tại \(D\) ta có: \(\begin{array}{*{20}{l}}{\sin \angle A = \frac{{CD}}{{CA}} \Rightarrow CD = CA.\sin \widehat A}\\{ \Rightarrow CD = 185.\sin {{53}^0}.}\\{\cos \widehat A = \frac{{AD}}{{AC}} \Rightarrow AD = CA.\cos \widehat A}\\{ \Rightarrow AD = 185.\cos {{53}^0}.}\\{ \Rightarrow BD = AB - AD = 234 - 185.\cos {{53}^0}.}\end{array}\) Áp dụng định lý Pitago cho \(\Delta BCD\) để tính BC. \(\begin{array}{*{20}{l}}{B{C^2} = B{D^2} + C{D^2} = {{\left( {234 - 185.\cos {{53}^0}} \right)}^2} + {{\left( {185.\sin {{53}^0}} \right)}^2}}\\{ \Leftrightarrow B{C^2} = {{234}^2} - 2.234.185\cos {{53}^0} + {{\left( {185.\cos {{53}^0}} \right)}^2} + {{\left( {185.\sin {{53}^0}} \right)}^2}}\\{ \Leftrightarrow B{C^2} = {{234}^2} - 2.234.185\cos {{53}^0} + {{185}^2}}\\{ \Leftrightarrow B{C^2} \approx 36875,86}\\{ \Rightarrow BC \approx 192{\mkern 1mu} m.}\end{array}\) 3)
a) \(AB.AD = AC.AE\) Áp dụng hệ thức lượng trong \(\Delta ABH\) vuông tại \(H\) có đường cao DH ta có: \(AB.AD = A{H^2}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)\) Áp dụng hệ thức lượng trong \(\Delta ACH\) vuông tại \(H\) có đường cao HE ta có: \(AE.AC = A{H^2}\left( 2 \right)\) Từ \(\left( 1 \right),{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right) \Rightarrow \)\(AB.AD = AC.AE{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( { = A{H^2}} \right).\) b) \(\frac{{A{B^2}}}{{A{C^2}}} = \frac{{BH}}{{CH}}\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao AH ta có: \(\left\{ {\begin{array}{*{20}{l}}{BH.BC = A{B^2}}\\{CH.BC = A{C^2}}\end{array}} \right..\) Ta có: \(\left. {\begin{array}{*{20}{l}}{A{B^2}.CH = BH.BC.CH}\\{A{C^2}.BH = CH.BC.BH}\end{array}} \right\} \Rightarrow A{B^2}.CH = A{C^2}.BH\)\( \Rightarrow \frac{{A{B^2}}}{{A{C^2}}} = \frac{{BH}}{{CH}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {dpcm} \right)\) Câu 5: Cho các số thực \(x,y > 0\) thỏa mãn \(\sqrt x + \sqrt y = 2\). Tìm giá trị nhỏ nhất của biều thức: \(P = x + y - 2022\sqrt {xy} \) Cách giải: Áp dụng bất đẳng thức Cô-si cho hai số dương \(\sqrt x ,\sqrt y \) ta có \(\begin{array}{l}2 = \sqrt x + \sqrt y \ge 2\sqrt {\sqrt x .\sqrt y } = 2\sqrt {\sqrt {xy} } \\ \Rightarrow \sqrt {xy} \le 1 \Rightarrow - 2022\sqrt {xy} \ge - 2022\,\,\,\left( 1 \right)\end{array}\) Áp dụng bất đẳng thức cô-si cho 2 số dương x, y ta có \(\begin{array}{l}x + y \ge 2\sqrt {xy} \\ \Rightarrow 2x + 2y \ge x + y + 2\sqrt {xy} = {(\sqrt x + \sqrt y )^2} = {2^2} = 4\\ \Rightarrow x + y \ge 2{\rm{ (2)}}\end{array}\) Cộng từng vế của (1) và (2) ta được \(P = x + y - 2022\sqrt {xy} \ge 2 - 2022 = - 2020.\) Dấu bằng xảy ra khi \(x = y = 1\). Vậy \({P_{\min }} = - 2020\) khi \(x = y = 1\).
|