Đề kiểm tra giữa kì 1 Toán 9 - Đề số 1 có lời giải chi tiếtĐề kiểm tra giữa kì 1 Toán 9 - Đề số 1 có lời giải chi tiết Đề bài Câu 1 (2 điểm): Tìm \(x\) để biểu thức sau xác định: a) \(\sqrt {x - 3} \) b) \(\sqrt { - \frac{2}{{2x - 1}}} \) Câu 2 (2 điểm): Thực hiện phép tính: a) \(\sqrt 5 .\sqrt {45} \) b) \(\sqrt {12} - \sqrt {27} + \sqrt 3 \) c) \(\sqrt {7 + 2\sqrt 6 } - \sqrt {7 - 2\sqrt 6 } \) Câu 3 (2 điểm): Giải phương trình: a) \(\sqrt {3x - 2} = 6\) b) \(\sqrt {{{\left( {x - 1} \right)}^2}} = 5\) Câu 4 (3,5 điểm): Cho tam giác \(ABC\) vuông tại \(A,\) có \(AB = 12cm,\) \(AC = 16cm.\) Kẻ đường cao \(AM.\) Kẻ \(ME \bot AB.\) a) Tính \(BC,\,\,\angle B,\,\,\angle C.\) b) Tính độ dài \(AM,\,\,BM.\) c) Chứng minh \(AE.AB = A{C^2} - M{C^2}.\) Câu 5 (0,5 điểm): a) Với \(a,\,\,b \ge 0.\) Chứng minh \(a + b \ge 2\sqrt {ab} .\) b) Áp dụng tính giá trị lớn nhất của biểu thức \(S = \sqrt {x - 2} + \sqrt {y - 3} ,\) biết \(x + y = 6.\) Lời giải chi tiết Câu 1 Phương pháp: Biểu thức \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\) Cách giải: a) \(\sqrt {x - 3} \) Biểu thức \(\sqrt {x - 3} \) xác định \( \Leftrightarrow x - 3 \ge 0\) \( \Leftrightarrow x \ge 3.\) Vậy \(x \ge 3\) thì biểu thức \(\sqrt {x - 3} \) xác định. b) \(\sqrt { - \frac{2}{{2x - 1}}} \) Biểu thức \(\sqrt { - \frac{2}{{2x - 1}}} \) xác định \( \Leftrightarrow - \frac{2}{{2x - 1}} \ge 0\) \( \Leftrightarrow 2x - 1 <0\) \( \Leftrightarrow x < \frac{1}{2}\) Vậy với \(x < \frac{1}{2}\) thì biểu thức \(\sqrt { - \frac{2}{{2x - 1}}} \) xác định. Câu 2 Phương pháp: Áp dụng các công thức: \(\sqrt A .\sqrt B = \sqrt {AB} ,\,\,A \ge 0,\,\,B \ge 0.\) \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,\,khi\,\,\,A < 0\end{array} \right.,\,\,B \ge 0.\) \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,khi\,\,\,A < 0\end{array} \right..\) Cách giải: a) \(\sqrt 5 .\sqrt {45} \) Ta có: \(\sqrt 5 .\sqrt {45} = \sqrt {5.45} = \sqrt {5.5.9} \) \( = \sqrt {{5^2}{{.3}^2}} = 5.3 = 15.\) b) \(\sqrt {12} - \sqrt {27} + \sqrt 3 \) Ta có: \(\begin{array}{l}\,\,\,\,\sqrt {12} - \sqrt {27} + \sqrt 3 \\ = \sqrt {{2^2}.3} - \sqrt {{3^2}.3} + \sqrt 3 \\ = 2\sqrt 3 - 3\sqrt 3 + \sqrt 3 = 0.\end{array}\) c) \(\sqrt {7 + 2\sqrt 6 } - \sqrt {7 - 2\sqrt 6 } \) Ta có: \(\begin{array}{l}\,\,\,\,\sqrt {7 + 2\sqrt 6 } - \sqrt {7 - 2\sqrt 6 } \\ = \sqrt {{{\left( {\sqrt 6 } \right)}^2} + 2\sqrt 6 + 1} - \sqrt {{{\left( {\sqrt 6 } \right)}^2} - 2\sqrt 6 + 1} \\ = \sqrt {{{\left( {\sqrt 6 + 1} \right)}^2}} - \sqrt {{{\left( {\sqrt 6 - 1} \right)}^2}} \\ = \left| {\sqrt 6 + 1} \right| - \left| {\sqrt 6 - 1} \right|\\ = \sqrt 6 + 1 - \left( {\sqrt 6 - 1} \right)\,\,\,\,\left( {do\,\,\sqrt 6 - 2 > 0} \right)\\ = \sqrt 6 + 1 - \sqrt 6 + 1\\ = 2.\end{array}\) Câu 3 Phương pháp: Giải phương trình: \(\sqrt {f\left( x \right)} = a\,\,\left( {a \ge 0} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\f\left( x \right) = {a^2}\end{array} \right..\) \(\sqrt {{{\left[ {f\left( x \right)} \right]}^2}} = a\,\,\left( {a \ge 0} \right)\) \( \Leftrightarrow \left| {f\left( x \right)} \right| = a\) \( \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\\f\left( x \right) = - a\end{array} \right..\) Cách giải: Giải phương trình: a) \(\sqrt {3x - 2} = 6\) Điều kiện: \(3x - 2 \ge 0\) \( \Leftrightarrow x \ge \frac{2}{3}\) Khi đó ta có phương trình \( \Leftrightarrow 3x - 2 = {6^2}\) \(\begin{array}{l} \Leftrightarrow 3x - 2 = 36\\ \Leftrightarrow 3x = 38\\ \Leftrightarrow x = \frac{{38}}{3}\,\,\,\left( {tm} \right)\end{array}\) Vậy phương trình có nghiệm duy nhất \(x = \frac{{38}}{3}.\) b) \(\sqrt {{{\left( {x - 1} \right)}^2}} = 5\) Điều kiện: \(x \in \mathbb{R}.\) \(\begin{array}{l}\,\,\,\,\,\,\,\,\sqrt {{{\left( {x - 1} \right)}^2}} = 5\\ \Leftrightarrow \left| {x - 1} \right| = 5\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 5\\x - 1 = - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 6\\x = - 4\end{array} \right.\end{array}\) Vậy phương trình có tập nghiệm: \(S = \left\{ { - 4;\,\,6} \right\}.\) Câu 4 Phương pháp: a) Sử dụng định lý Pitago để tính \(BC = \sqrt {A{B^2} + A{C^2}} .\) Sử dụng các công thức về tỉ số lượng giác của góc nhọn trong tam giác vuông và định lý tổng số đo của 3 góc trong tam giác để tính số đo của \(\angle B,\,\,\angle C.\) b) Áp dụng hệ thức lượng trong tam giác \(ABC\) vuông tại \(A,\) có đường cao \(AM\) ta có: \(AM.BC = AB.AC\) và \(A{B^2} = BM.BC.\) c) Áp dụng hệ thức lượng trong tam giác \(AMB\) vuông tại \(A,\) có đường cao \(ME\) ta có: \(A{M^2} = AE.AB\) và định lý Pitago cho \(\Delta AMC\) vuông tại \(M\) để chứng minh đẳng thức đề bài yêu cầu. Cách giải:
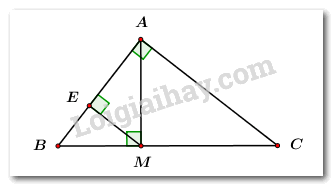
a) Tính \(BC,\,\,\angle B,\,\,\angle C.\) Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có: \(BC = \sqrt {A{B^2} + A{C^2}} \) \( = \sqrt {{{12}^2} + {{16}^2}} = \sqrt {400} \) \( = 20\,\,cm.\) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\sin \angle B = \frac{{AC}}{{BC}} = \frac{{16}}{{20}} = 0,8\) \( \Rightarrow \angle B \approx {53^0}.\) \( \Rightarrow \angle C = {90^0} - \angle B\) \( = {90^0} - {53^0} = {37^0}.\) b) Tính độ dài \(AM,\,\,BM.\) Áp dụng hệ thức lượng trong tam giác \(ABC\) vuông tại \(A,\) có đường cao \(AM\) ta có: \(AM.BC = AB.AC\) \( \Rightarrow AM = \frac{{AB.AC}}{{BC}} = \frac{{12.16}}{{20}} = 9.6\,\,\left( {cm} \right).\) Lại có: \(A{B^2} = BM.BC\) \( \Rightarrow BM = \frac{{A{B^2}}}{{BC}} = \frac{{{{12}^2}}}{{20}} = 7,2\,\,cm.\) Vậy \(AM = 9,6\,\,cm\) và \(BM = 7,2\,\,cm.\) c) Chứng minh \(AE.AB = A{C^2} - M{C^2}.\) Áp dụng hệ thức lượng trong tam giác \(AMB\) vuông tại \(A,\) có đường cao \(ME\) ta có: \(A{M^2} = AE.AB\) Áp dụng định lý Pitago cho \(\Delta AMC\) vuông tại \(M\) ta có: \(A{M^2} = A{C^2} - M{C^2}\) \( \Rightarrow AE.AB = A{C^2} - M{C^2}\,\,\left( { = A{M^2}} \right)\,\,\left( {dpcm} \right).\) Câu 5 Phương pháp: a) Áp dụng hằng đẳng thức: \({\left( {\sqrt a - \sqrt b } \right)^2} \ge 0\,\,\,\forall a,\,\,b \ge 0.\) b) Áp dụng bất đẳng thức \(a + b \ge 2\sqrt {ab} \) khi \(a,\,\,b \ge 0\) để tìm GTLN của biểu thức. Cách giải: a) Với \(a,\,\,b \ge 0.\) Chứng minh \(a + b \ge 2\sqrt {ab} .\) Với mọi \(a,\,\,b \ge 0\) ta có: \({\left( {\sqrt a - \sqrt b } \right)^2} \ge 0\) \( \Leftrightarrow a - 2\sqrt {ab} + b \ge 0\) \( \Leftrightarrow a + b \ge 2\sqrt {ab} \,\,\,\left( {dpcm} \right).\) Dấu “=” xảy ra \( \Leftrightarrow a = b.\) b) Áp dụng tính giá trị lớn nhất của biểu thức \(S = \sqrt {x - 2} + \sqrt {y - 3} ,\) biết \(x + y = 6.\) Điều kiện: \(x \ge 2,\,\,y \ge 3.\) Ta có: \(S = \sqrt {x - 2} + \sqrt {y - 3} \) \[\begin{array}{l} \Rightarrow {S^2} = x - 2 + y - 3 + 2\sqrt {\left( {x - 2} \right)\left( {y - 3} \right)} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = x + y - 5 + 2\sqrt {\left( {x - 2} \right)\left( {y - 3} \right)} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 6 - 5 + 2\sqrt {\left( {x - 2} \right)\left( {y - 3} \right)} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 1 + 2\sqrt {\left( {x - 2} \right)\left( {y - 3} \right)} .\end{array}\] Áp dụng bất đẳng thức \(a + b \ge 2\sqrt {ab} \) với \(a,\,\,b \ge 0\) ta có: \(2\sqrt {\left( {x - 2} \right)\left( {y - 3} \right)} \le x - 2 + y - 3 = 6 - 5 = 1\) \( \Rightarrow {S^2} = 1 + 2\sqrt {\left( {x - 2} \right)\left( {y - 3} \right)} \le 1 + 1 = 2\) \( \Rightarrow {S^2} \le 2 \Rightarrow S \le \sqrt 2 .\) Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x - 2 = y - 3\\x + y = 6\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x - y = - 1\\x + y = 6\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{5}{2}\,\,\left( {tm} \right)\\y = \frac{7}{2}\,\,\left( {tm} \right)\end{array} \right.\) Vậy giá trị lớn nhất của \(S = \sqrt 2 \) khi \(\left( {x;\,\,y} \right) = \left( {\frac{5}{2};\,\,\frac{7}{2}} \right).\)
|