Đề kiểm tra giữa kì 1 Toán 9 - Đề số 11 có lời giải chi tiếtTải về Đề kiểm tra giữa kì 1 Toán 9 - Đề số 11 có lời giải chi tiết Đề bài Câu 1: Tính a) \(\sqrt {50} + \sqrt {32} - 3\sqrt {18} + 4\sqrt 8 \) b) \(\frac{{5 - 2\sqrt 5 }}{{\sqrt 5 - 2}} - \sqrt {6 - 2\sqrt 5 } \) Câu 2: Giải phương trình a) \(\sqrt {4{x^2} - 4x + 1} = 5\) b) \(3\sqrt {x - 2} - \sqrt {4x - 8} + 4\sqrt {\frac{{9x - 18}}{4}} = 14\) c) \(\sqrt[3]{{4x - 1}} = 3\) Câu 3: Cho hai biểu thức \(A = \frac{{\sqrt x {\rm{ \;}} + 2}}{{\sqrt x {\rm{ \;}} - 2}}\) và \(B = \frac{3}{{\sqrt x {\rm{ \;}} + 2}} - \frac{{\sqrt x {\rm{ \;}} + 10}}{{x - 4}}\) (với \(x \ge 0,x \ne 4\)) a) Tính giá trị của A khi x = 9. b) Rút gọn biểu thức B. c) Cho biểu thức P = A.B. Tìm tất cả các giá trị của x để \(P \le {\rm{ \;}} - 1\). Câu 4: Hãy tính chiều cao của tháp Eiffel mà không cần lên tận đỉnh tháp khi biết góc tạo bởi tia nắng mặt trời với mặt đất là \({62^0}\) và bóng của tháp trên mặt đất khi đó là 172m (làm tròn kết quả tới chữ số thập phân thứ nhất)
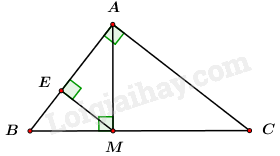
Câu 5: Cho tam giác ABC vuông tại A, có AB = 12cm, AC = 16cm. Kẻ đường cao AM. Kẻ \(ME \bot AB.\) a) Tính \(BC,{\mkern 1mu} {\mkern 1mu} \widehat B,{\mkern 1mu} {\mkern 1mu} \widehat C.\) b) Tính độ dài \(AM,{\mkern 1mu} {\mkern 1mu} BM.\) c) Chứng minh \(AE.AB = A{C^2} - M{C^2}.\) Câu 6: Chứng minh rằng nếu \(xyz = 1\) thì \(\frac{1}{{1 + x + xy}} + \frac{1}{{1 + y + yz}} + \frac{1}{{1 + z + zx}} = 1\). -------- Hết -------- Lời giải chi tiết Câu 1: Tính a) \(\sqrt {50} + \sqrt {32} - 3\sqrt {18} + 4\sqrt 8 \) b) \(\frac{{5 - 2\sqrt 5 }}{{\sqrt 5 - 2}} - \sqrt {6 - 2\sqrt 5 } \) Phương pháp: Công thức khai phương căn bậc hai, trục căn thức. Lời giải: a) \(\sqrt {50} + \sqrt {32} - 3\sqrt {18} + 4\sqrt 8 \) \(\begin{array}{l} = \sqrt {25.2} + \sqrt {16.2} - 3\sqrt {9.2} + 4\sqrt {4.2} \\ = 5\sqrt 2 + 4\sqrt 2 - 9\sqrt 2 + 8\sqrt 2 \\ = 8\sqrt 2 \end{array}\) b) \(\frac{{5 - 2\sqrt 5 }}{{\sqrt 5 - 2}} - \sqrt {6 - 2\sqrt 5 } \) \(\begin{array}{l} = \frac{{\sqrt 5 \left( {\sqrt 5 - 2} \right)}}{{\sqrt 5 - 2}} - \sqrt {5 - 2\sqrt 5 + 1} \\ = \sqrt 5 - \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} \\ = \sqrt 5 - \left| {\sqrt 5 - 1} \right|\\ = \sqrt 5 - \sqrt 5 + 1\\ = 1\end{array}\) Câu 2: Giải phương trình a) \(\sqrt {4{x^2} - 4x + 1} = 5\) b) \(3\sqrt {x - 2} - \sqrt {4x - 8} + 4\sqrt {\frac{{9x - 18}}{4}} = 14\) c) \(\sqrt[3]{{4x - 1}} = 3\) Phương pháp: a) Đưa về phương trình trị tuyệt đối chia hai trường hợp b) Tìm điều kiện xác định, đưa các hệ số ra ngoài căn và rút gọn c) Lập phương 2 vế của phương trình Lời giải: a) \(\sqrt {4{x^2} - 4x + 1} = 5\) \(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {2x - 1} \right)}^2}} = 5\\ \Leftrightarrow \left| {2x - 1} \right| = 5\\ \Leftrightarrow \left[ \begin{array}{l}2x - 1 = 5\\2x - 1 = - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 6\\2x = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 2\end{array} \right.\end{array}\) Vậy \(S = \left\{ { - 2,3} \right\}\) b) \(3\sqrt {x - 2} - \sqrt {4x - 8} + 4\sqrt {\frac{{9x - 18}}{4}} = 14\) TXĐ: \(x \ge 2\) \(\begin{array}{l}pt \Leftrightarrow 3\sqrt {x - 2} - \sqrt {4\left( {x - 2} \right)} + 4\sqrt {\frac{{9\left( {x - 2} \right)}}{4}} = 14\\ \Leftrightarrow 3\sqrt {x - 2} - 2\sqrt {x - 2} + 6\sqrt {x - 2} = 14\\ \Leftrightarrow 7\sqrt {x - 2} = 14\\ \Leftrightarrow \sqrt {x - 2} = 2\\ \Leftrightarrow x - 2 = 4\\ \Leftrightarrow x = 6\left( {tm} \right)\end{array}\) Vậy \(S = \left\{ 6 \right\}\) c) \(\sqrt[3]{{4x - 1}} = 3\) TXĐ: \(\forall x \in \mathbb{R}\) \(\begin{array}{l}pt \Leftrightarrow 4x - 1 = {3^3}\\ \Leftrightarrow 4x - 1 = 27\\ \Leftrightarrow 4x = 28\\ \Leftrightarrow x = 7\\ \Rightarrow S = \left\{ 7 \right\}\end{array}\) Câu 3: Cho hai biểu thức \(A = \frac{{\sqrt x {\rm{ \;}} + 2}}{{\sqrt x {\rm{ \;}} - 2}}\) và \(B = \frac{3}{{\sqrt x {\rm{ \;}} + 2}} - \frac{{\sqrt x {\rm{ \;}} + 10}}{{x - 4}}\) (với \(x \ge 0,x \ne 4\)) a) Tính giá trị của A khi x = 9. b) Rút gọn biểu thức B. c) Cho biểu thức P = A.B. Tìm tất cả các giá trị của x để \(P \le {\rm{ \;}} - 1\). Phương pháp: a) Kiểm tra x = 9 có thỏa mãn điều kiện hay không, sau đó thay vào biểu thức A để tính. b) Xác định mẫu thức chung, quy đồng và thực hiện các phép toán với các phân thức đại số. c) Tính P = A.B. Biến đổi \(P \le {\rm{ \;}} - 1\) \( \Leftrightarrow P + 1 \le 0\) \(\frac{{f\left( x \right)}}{{g\left( x \right)}} \le 0\) \( \Leftrightarrow f\left( x \right) \ge 0,g\left( x \right) < 0\) hoặc \(f\left( x \right) \le 0,g\left( x \right) > 0\) Lời giải: a) Với \(x = 9\left( {tmdk} \right)\) thay vào A ta được: \(A = \frac{{\sqrt 9 {\rm{ \;}} + 2}}{{\sqrt 9 {\rm{ \;}} - 2}} = \frac{{3 + 2}}{{3 - 2}} = \frac{5}{1} = 5\) Vậy \(x = 9\) thì \(A = 5\). b) \(B = \frac{3}{{\sqrt x {\rm{ \;}} + 2}} - \frac{{\sqrt x {\rm{ \;}} + 10}}{{x - 4}}\) \( = \frac{3}{{\sqrt x {\rm{\;}} + 2}} - \frac{{\sqrt x {\rm{\;}} + 10}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} + 2} \right)}} = \frac{{3\left( {\sqrt x {\rm{\;}} - 2} \right) - \left( {\sqrt x {\rm{\;}} + 10} \right)}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} + 2} \right)}}\) \( = \frac{{3\sqrt x {\rm{\;}} - 6 - \sqrt x {\rm{\;}} - 10}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} + 2} \right)}} = \frac{{2\sqrt x {\rm{\;}} - 16}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} + 2} \right)}}\) Vậy \(B = \frac{{2\sqrt x {\rm{ \;}} - 16}}{{\left( {\sqrt x {\rm{ \;}} - 2} \right)\left( {\sqrt x {\rm{ \;}} + 2} \right)}}\) với \(x \ge 0,x \ne 4\). c) Ta có: \(\begin{array}{*{20}{l}}{P = A.B}\\{P = \frac{{\sqrt x {\rm{ \;}} + 2}}{{\sqrt x {\rm{ \;}} - 2}}.\frac{{2\sqrt x {\rm{ \;}} - 16}}{{\left( {\sqrt x {\rm{ \;}} - 2} \right)\left( {\sqrt x {\rm{ \;}} + 2} \right)}}}\\{P = \frac{{2\sqrt x {\rm{ \;}} - 16}}{{{{\left( {\sqrt x {\rm{ \;}} - 2} \right)}^2}}}}\end{array}\) Để \(P \le {\rm{ \;}} - 1\)\( \Leftrightarrow \frac{{2\sqrt x {\rm{ \;}} - 16}}{{{{\left( {\sqrt x {\rm{ \;}} - 2} \right)}^2}}} \le {\rm{ \;}} - 1\) \(\begin{array}{*{20}{l}}{ \Leftrightarrow \frac{{2\sqrt x {\rm{ \;}} - 16}}{{{{\left( {\sqrt x {\rm{ \;}} + 2} \right)}^2}}} + 1 \le 0}\\{ \Leftrightarrow \frac{{2\sqrt x {\rm{ \;}} - 16 + x + 4\sqrt x {\rm{ \;}} + 4}}{{{{\left( {\sqrt x {\rm{ \;}} + 2} \right)}^2}}} \le 0}\\{ \Leftrightarrow \frac{{x + 6\sqrt x {\rm{ \;}} - 12}}{{{{\left( {\sqrt x {\rm{ \;}} + 2} \right)}^2}}} \le 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( * \right)}\end{array}\) Vì \(x \ge 0,x \ne 4 \Rightarrow \sqrt x {\rm{ \;}} + 2 \ge 2 \Rightarrow {\left( {\sqrt x {\rm{ \;}} + 2} \right)^2} \ge 4 > 0\) Do đó \(\left( * \right) \Leftrightarrow x + 6\sqrt x {\rm{ \;}} - 12 \le 0\) \(\begin{array}{*{20}{l}}{ \Leftrightarrow x + 6\sqrt x {\rm{ \;}} + 9 - 21 \le 0}\\{ \Leftrightarrow {{\left( {\sqrt x {\rm{ \;}} + 3} \right)}^2} - 21 \le 0}\\{ \Leftrightarrow {\rm{ \;}} - \sqrt {21} {\rm{ \;}} \le \sqrt x {\rm{ \;}} + 3 \le \sqrt {21} }\\{ \Leftrightarrow {\rm{ \;}} - \sqrt {21} {\rm{ \;}} - 3 \le \sqrt x {\rm{ \;}} \le \sqrt {21} {\rm{ \;}} - 3}\\{ \Leftrightarrow \sqrt x {\rm{ \;}} \le \sqrt {21} {\rm{ \;}} - 3}\\{ \Leftrightarrow x \le {{\left( {\sqrt {21} {\rm{ \;}} - 3} \right)}^2}}\\{ \Leftrightarrow x \le 30 - 6\sqrt {21} }\end{array}\) Kết hợp điều kiện: \(x \ge 0,x \ne 4\) ta có \(0 \le x \le 30 - 6\sqrt {21} \). Vậy \(0 \le x \le 30 - 6\sqrt {21} \). Câu 4: Hãy tính chiều cao của tháp Eiffel mà không cần lên tận đỉnh tháp khi biết góc tạo bởi tia nắng mặt trời với mặt đất là \({62^0}\) và bóng của tháp trên mặt đất khi đó là 172m (làm tròn kết quả tới chữ số thập phân thứ nhất)
Phương pháp: Vận dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải: Bài toán được mô tả như hình vẽ Chiều cao của tháp Eiffel là độ dài đoạn BH Tam giác ABH vuông tại H nên ta có \(BH = AH.\tan \widehat {BAH}\) (Hệ thức lượng trong tam giác vuông) \( \Rightarrow BH = 172.\tan {62^0} = 323,5m\) Vậy chiều cao của tháp Eiffel là 323,5m Câu 5: Cho tam giác ABC vuông tại A, có AB = 12cm, AC = 16cm. Kẻ đường cao AM. Kẻ \(ME \bot AB.\) a) Tính \(BC,{\mkern 1mu} {\mkern 1mu} \widehat B,{\mkern 1mu} {\mkern 1mu} \widehat C.\) b) Tính độ dài \(AM,{\mkern 1mu} {\mkern 1mu} BM.\) c) Chứng minh \(AE.AB = A{C^2} - M{C^2}.\) Phương pháp: a) Sử dụng định lý Pitago để tính \(BC = \sqrt {A{B^2} + A{C^2}} .\) Sử dụng các công thức về tỉ số lượng giác của góc nhọn trong tam giác vuông và định lý tổng số đo của 3 góc trong tam giác để tính số đo của \(\widehat B,{\mkern 1mu} {\mkern 1mu} \widehat C.\) b) Áp dụng hệ thức lượng trong tam giác ABC vuông tại A, có đường cao AM ta có: \(AM.BC = AB.AC\) và \(A{B^2} = BM.BC.\) c) Áp dụng hệ thức lượng trong tam giác AMB vuông tại A, có đường cao ME ta có: \(A{M^2} = AE.AB\) và định lý Pitago cho \(\Delta AMC\) vuông tại M để chứng minh đẳng thức đề bài yêu cầu. Lời giải: a) Tính \(BC,{\mkern 1mu} {\mkern 1mu} \widehat B,{\mkern 1mu} {\mkern 1mu} \widehat C.\) Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có: \(BC = \sqrt {A{B^2} + A{C^2}} \) \( = \sqrt {{{12}^2} + {{16}^2}} {\rm{\;}} = \sqrt {400} \) \( = 20{\mkern 1mu} {\mkern 1mu} cm.\) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\sin \widehat B = \frac{{AC}}{{AB}} = \frac{{16}}{{20}} = 0,8\) \( \Rightarrow \widehat B \approx {53^0}.\) \( \Rightarrow \widehat C = {90^0} - \widehat B\) \( = {90^0} - {53^0} = {37^0}.\) b) Tính độ dài \(AM,{\mkern 1mu} {\mkern 1mu} BM.\) Áp dụng hệ thức lượng trong tam giác ABC vuông tại A, có đường cao AM ta có: \(AM.BC = AB.AC\) \( \Rightarrow AM = \frac{{AB.AC}}{{BC}} = \frac{{12.16}}{{20}} = 9.6{\mkern 1mu} {\mkern 1mu} \left( {cm} \right).\) Lại có: \(A{B^2} = BM.BC\) \( \Rightarrow BM = \frac{{A{B^2}}}{{BC}} = \frac{{{{12}^2}}}{{20}} = 7,2{\mkern 1mu} {\mkern 1mu} cm.\) Vậy \(AM = 9,6{\mkern 1mu} {\mkern 1mu} cm\) và \(BM = 7,2{\mkern 1mu} {\mkern 1mu} cm.\) c) Chứng minh \(AE.AB = A{C^2} - M{C^2}.\) Áp dụng hệ thức lượng trong tam giác AMB vuông tại A, có đường cao ME ta có: \(A{M^2} = AE.AB\) Áp dụng định lý Pitago cho \(\Delta AMC\) vuông tại \(M\) ta có: \(A{M^2} = A{C^2} - M{C^2}\) \( \Rightarrow AE.AB = A{C^2} - M{C^2}{\mkern 1mu} {\mkern 1mu} \left( { = A{M^2}} \right){\mkern 1mu} {\mkern 1mu} \left( {dpcm} \right).\) Câu 6: Chứng minh rằng nếu \(xyz = 1\) thì \(\frac{1}{{1 + x + xy}} + \frac{1}{{1 + y + yz}} + \frac{1}{{1 + z + zx}} = 1\). Phương pháp: Sử dụng linh hoạt giả thiết \(xyz = 1\), chứng minh \(\begin{array}{*{20}{l}}{\frac{1}{{1 + x + xy}} + \frac{1}{{1 + y + yz}} = \frac{{yz + 1}}{{1 + y + yz}}}\\{\frac{1}{{1 + z + zx}} = \frac{y}{{y + yz + 1}}}\end{array}\) Lời giải: \(\begin{array}{*{20}{l}}{\frac{1}{{1 + x + xy}} + \frac{1}{{1 + y + yz}} = \frac{1}{{xyz + x + xy}} + \frac{1}{{1 + y + yz}} = \frac{{xyz}}{{x\left( {yz + 1 + y} \right)}} + \frac{1}{{1 + y + yz}} = \frac{{yz + 1}}{{1 + y + yz}}}\\{\frac{1}{{1 + z + zx}} = \frac{{xyz}}{{xzy + z.\left( {xyz} \right) + zx}} = \frac{{xyz}}{{xz\left( {y + yz + 1} \right)}} = \frac{y}{{y + yz + 1}}}\end{array}\) Suy ra :\(\frac{1}{{1 + x + xy}} + \frac{1}{{1 + y + yz}} + \frac{1}{{1 + z + zx}} = \frac{{yz + 1}}{{1 + y + yz}} + \frac{y}{{y + yz + 1}} = \frac{{1 + y + yz}}{{1 + y + yz}} = 1\) (đpcm)
|