Đề số 10 - Đề kiểm tra học kì 1 - Toán 9Tải vềĐáp án và lời giải chi tiết Đề số 10 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
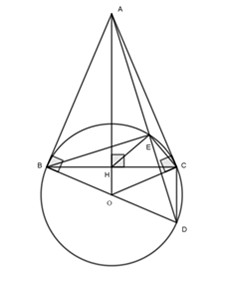
Đề bài Câu 1 (2,0 điểm): Hãy tính giá trị của: a) M=(2√300+3√48−4√75):√3 ; b) N=√(√3−2)2+√4−2√3 ; c) P=2√3+1−1√3−2+12√3+3 ; Câu 2 (2,0 điểm): Cho các biểu thức: A=1−√x1+√x và B=√x+3√x−2+√x+23−√x+√x+2x−5√x+6 với x≥0,x≠4,x≠9. a) Hãy tính giá trị của A khi x=16. b) Rút gọn B. c) Xét biểu thức T=AB . Hãy tìm giá trị nhỏ nhất của T. Câu 3 (2,0 điểm): Cho hàm số y=(2−m)x+m+1 (với m là tham số và m≠2) có đồ thị là đường thẳng (d). a) Khi m=0, hãy vẽ (d) trên hệ trục tọa độ Oxy. b) Tìm m để (d) cắt đường thẳng y=2x−5 tại điểm có hoành độ bằng 2. c) Tìm m để (d) cùng với các trục tọa độ Ox,Oy tạo thành một tam giác có diện tích bằng 2. Câu 4 (3,5 điểm): Cho đường tròn (O;R) và điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn. b) Chứng minh OA là đường trung trực của BC. c) Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) (E không trùng với D). Chứng minh DEBE=BDBA. d) Tính số đo góc HEC. Câu 5 (0,5 điểm): Cho x>0,y>0 thỏa mãn xy=6. Tìm giá trị nhỏ nhất của biểu thức: Q=2x+3y+63x+2y . LG bài 1 Lời giải chi tiết: a) M=(2√300+3√48−4√75):√3 M=(2√300+3√48−4√75):√3=(2.10√3+3.4√3−4.5√3):√3=(20√3+12√3−20√3):√3=12√3:√3=12 b) N=√(√3−2)2+√4−2√3 ; N=√(√3−2)2+√4−2√3=|√3−2|+√(√3−1)2=2−√3+|√3−1|=2−√3+√3−1=1 c) P=2√3+1−1√3−2+12√3+3 ; P=2√3+1−1√3−2+12√3+3=2(√3−1)(√3+1)(√3−1)−1(√3+2)(√3−2)(√3+2)+12(3−√3)(3+√3)(3−√3)=2(√3−1)2−√3+2−1+12(3−√3)6=√3−1+√3+2+2(3−√3)=7 LG bài 2 Lời giải chi tiết: Câu 2: Cho các biểu thức: A=1−√x1+√x và B=√x+3√x−2+√x+23−√x+√x+2x−5√x+6 với x≥0,x≠4,x≠9. a) Hãy tính giá trị của A khi x=16. Tại x=16thì A=1−√161+√16=1−41+4=1−45=15 b) Rút gọn B. B=√x+3√x−2+√x+23−√x+√x+2x−5√x+6=√x+3√x−2−√x+2√x−3+√x+2(√x−2)(√x−3)=(√x+3)(√x−3)−(√x+2)(√x−2)+√x+2(√x−2)(√x−3)=x−9−x+4+√x+2(√x−2)(√x−3)=√x−3(√x−2)(√x−3)=1√x−2 c) Xét biểu thức T=AB . Hãy tìm giá trị nhỏ nhất của T. A=1−√x1+√x=1+√x−√x1+√x=11+√x T=AB=11+√x:1√x−2=√x−21+√x=√x+1−31+√x=1−31+√x Do x≥0⇒√x≥0⇒31+√x≤31=3⇒T=1−31+√x≥1−3=−2 Dấu bằng xảy ra khi x=0 Vậy MinT=−2 khi x=0. LG bài 3 Lời giải chi tiết: Câu 3: Cho hàm số y=(2−m)x+m+1 (với m là tham số và m≠2) có đồ thị là đường thẳng (d).
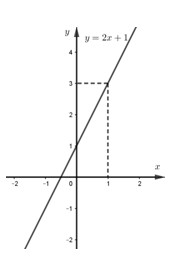
a) Khi m=0, hãy vẽ (d) trên hệ trục tọa độ Oxy. Khim=0 thì (d):y=2x+1 Đồ thị của đường thẳng (d) đi qua 2 điểm (0;1),(1;3). b) Tìm m để (d) cắt đường thẳng y=2x−5 tại điểm có hoành độ bằng 2. Phương trình hoành độ giao điểm của (d) và đường thẳng y=2x−5 là (2−m)x+m+1=2x−5⇔mx=m+6(1) Để (d) cắt đường thẳng y=2x−5 tại điểm có hoành độ bằng 2 thì x=2 là nghiệm của phương trình (1) hay 2m=m+6⇔m=6. Vậy với m=6 thỏa mãn yêu cầu đề bài. c) Tìm m để (d) cùng với các trục tọa độ Ox,Oy tạo thành một tam giác có diện tích bằng 2. Gọi A và B là giao điểm của (d) lần lượt với hai trục tọa độ Ox, Oy. Tọa độ điểm A thỏa mãn {y=(2−m)x+m+1y=0⇔x=m+1m−2 ⇒A(m+1m−2;0)⇒OA=|m+1m−2| Tọa độ điểm B thỏa mãn {y=(2−m)x+m+1x=0⇔y=m+1 ⇒B(0;m+1)⇒OB=|m+1| SΔOAB=2⇔OA.OB2=2 ⇔|m+1m−2|.|m+1|=4 ⇔(m+1)2=4|m−2| Trường hợp 1: m>2⇒pt⇔(m+1)2=4(m−2)⇔m2−2m+9=0 vô nghiệm. Trường hợp 2: m<2⇒pt⇔(m+1)2=−4(m−2)⇔m2+6m−7=0 ⇔[m=1(tm)m=−7(tm) Vậy với m=1 hoặc m=−7 thỏa mãn yêu cầu đề bài. LG bài 4 Lời giải chi tiết: Câu 4: Cho đường tròn (O;R) và điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn. Ta có AB, AC là hai tiếp tuyến của (O)⇒∠OBA=∠OCA=90o ⇒B, C cùng thuộc đường tròn đường kính OA ⇒ A, B, O, C cùng thuộc một đường tròn đường kính OA. (đpcm) b) Chứng minh OA là đường trung trực của BC. Ta có AB, AC là hai tiếp tuyến của (O) cắt nhau tại A ⇒AB=AC và AO là phân giác ∠BAC (tính chất 2 tiếp tuyến cắt nhau) ⇒ΔABC là tam giác cân tại A ⇒AO vừa là phân giác ∠BAC vừa là đường trung trực của BC (tính chất tam giác cân) c) Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) (E không trùng với D). Chứng minh DEBE=BDBA. Ta có D đối xứng với B qua O⇒BD là đường kính của (O) ⇒∠BED=90o (góc nội tiếp chắn nửa đường tròn) Xét ΔBED và ΔABD có: ∠BED=∠ABD=90o, ∠D chung d) Tính số đo góc HEC. ∠BCD=90o (góc nội tiếp chắn nửa đường tròn) ∠AHB=90o (AO là trung trực của BC) Xét ΔBCD và ΔAHB có: ∠BCD=∠AHB=90o,∠BDC=∠ABH(BA là tiếp tuyến của (O) tại B) kết hợp c) ⇒DEBE=CDBH Xét ΔBHE và ΔDCE có (2 góc t.ư) ⇒∠BEH+∠HED=∠DEC+∠HED⇒∠BED=∠HEC Mà ∠BED=90o (chứng minh trên) Vậy ∠HEC=90o LG bài 5 Lời giải chi tiết: Cho x>0,y>0 thỏa mãn xy=6. Tìm giá trị nhỏ nhất của biểu thức: Q=2x+3y+63x+2y . Q=2x+3y+63x+2y=2y+3xxy+63x+2y=3x+2y6+63x+2y Đặt t=3x+2y⇒t≥2√3x.2y⇔t≥2√6.6=12 Theo bất đẳng thức AM-GM và vì t≥12 nên ta có: Q=t6+6t=(t6+24t)−18t≥2√t6.24t−1812=52 Dấu “=” xảy ra khi {3x=2yxy=6⇔{x=2y32y23=6⇔{x=2y3y2=9⇔{x=2y=3(doy>0) Vậy giá trị nhỏ nhất của Q là 52 đạt được khi {x=2y=3. Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 9 tại HocTot.Nam.Name.Vn HocTot.Nam.Name.Vn
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|